An Empirical Comparison of V-fold Penalisation and Cross Validation for Model Selection in Distribution-Free Regression

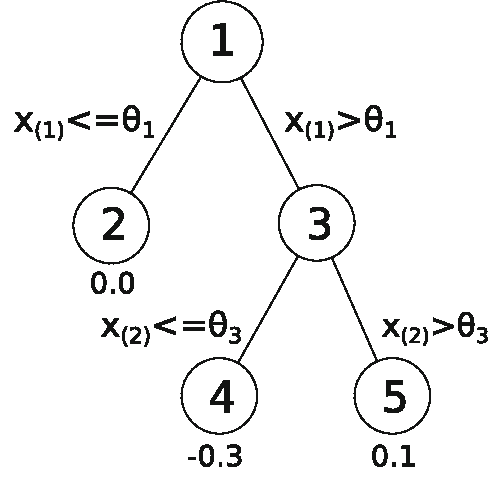
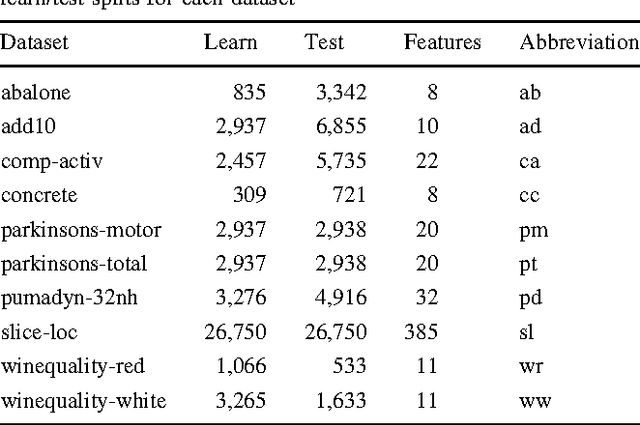
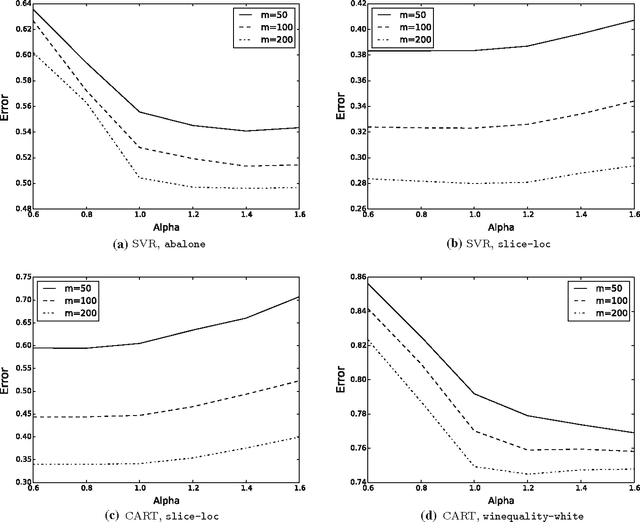
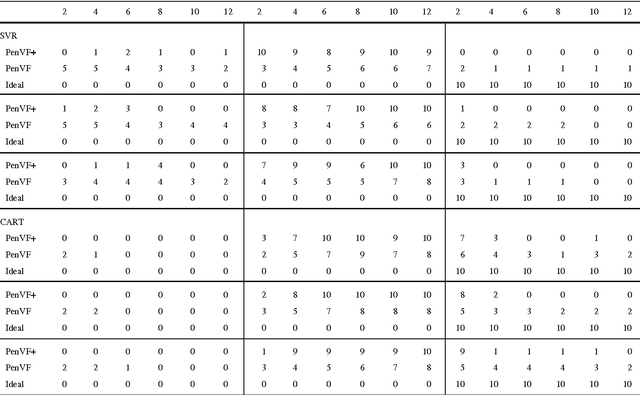
Model selection is a crucial issue in machine-learning and a wide variety of penalisation methods (with possibly data dependent complexity penalties) have recently been introduced for this purpose. However their empirical performance is generally not well documented in the literature. It is the goal of this paper to investigate to which extent such recent techniques can be successfully used for the tuning of both the regularisation and kernel parameters in support vector regression (SVR) and the complexity measure in regression trees (CART). This task is traditionally solved via V-fold cross-validation (VFCV), which gives efficient results for a reasonable computational cost. A disadvantage however of VFCV is that the procedure is known to provide an asymptotically suboptimal risk estimate as the number of examples tends to infinity. Recently, a penalisation procedure called V-fold penalisation has been proposed to improve on VFCV, supported by theoretical arguments. Here we report on an extensive set of experiments comparing V-fold penalisation and VFCV for SVR/CART calibration on several benchmark datasets. We highlight cases in which VFCV and V-fold penalisation provide poor estimates of the risk respectively and introduce a modified penalisation technique to reduce the estimation error.