Robust Consensus in Ranking Data Analysis: Definitions, Properties and Computational Issues

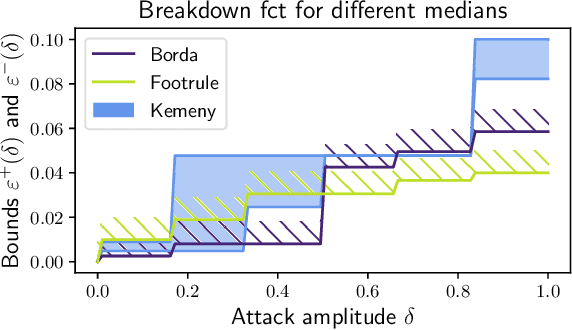
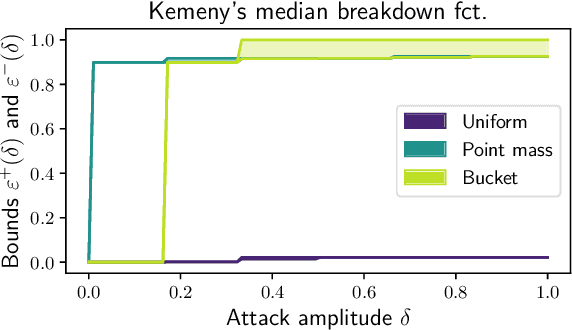
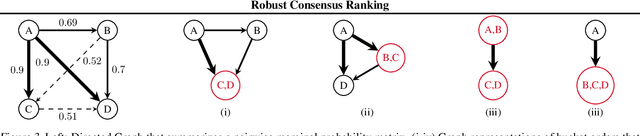
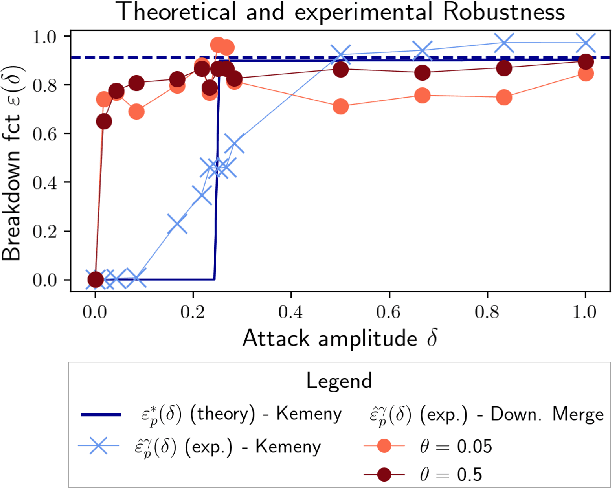
As the issue of robustness in AI systems becomes vital, statistical learning techniques that are reliable even in presence of partly contaminated data have to be developed. Preference data, in the form of (complete) rankings in the simplest situations, are no exception and the demand for appropriate concepts and tools is all the more pressing given that technologies fed by or producing this type of data (e.g. search engines, recommending systems) are now massively deployed. However, the lack of vector space structure for the set of rankings (i.e. the symmetric group $\mathfrak{S}_n$) and the complex nature of statistics considered in ranking data analysis make the formulation of robustness objectives in this domain challenging. In this paper, we introduce notions of robustness, together with dedicated statistical methods, for Consensus Ranking the flagship problem in ranking data analysis, aiming at summarizing a probability distribution on $\mathfrak{S}_n$ by a median ranking. Precisely, we propose specific extensions of the popular concept of breakdown point, tailored to consensus ranking, and address the related computational issues. Beyond the theoretical contributions, the relevance of the approach proposed is supported by an experimental study.

An Adversarial Robustness Perspective on the Topology of Neural Networks

In this paper, we investigate the impact of neural networks (NNs) topology on adversarial robustness. Specifically, we study the graph produced when an input traverses all the layers of a NN, and show that such graphs are different for clean and adversarial inputs. We find that graphs from clean inputs are more centralized around highway edges, whereas those from adversaries are more diffuse, leveraging under-optimized edges. Through experiments on a variety of datasets and architectures, we show that these under-optimized edges are a source of adversarial vulnerability and that they can be used to detect adversarial inputs.

Origins of Low-dimensional Adversarial Perturbations

In this note, we initiate a rigorous study of the phenomenon of low-dimensional adversarial perturbations in classification. These are adversarial perturbations wherein, unlike the classical setting, the attacker's search is limited to a low-dimensional subspace of the feature space. The goal is to fool the classifier into flipping its decision on a nonzero fraction of inputs from a designated class, upon the addition of perturbations from a subspace chosen by the attacker and fixed once and for all. It is desirable that the dimension $k$ of the subspace be much smaller than the dimension $d$ of the feature space, while the norm of the perturbations should be negligible compared to the norm of a typical data point. In this work, we consider binary classification models under very general regularity conditions, which are verified by certain feedforward neural networks (e.g., with sufficiently smooth, or else ReLU activation function), and compute analytical lower-bounds for the fooling rate of any subspace. These bounds explicitly highlight the dependence that the fooling rate has on the margin of the model (i.e., the ratio of the output to its $L_2$-norm of its gradient at a test point), and on the alignment of the given subspace with the gradients of the model w.r.t. inputs. Our results provide a theoretical explanation for the recent success of heuristic methods for efficiently generating low-dimensional adversarial perturbations. Moreover, our theoretical results are confirmed by experiments.

Statistical Depth Functions for Ranking Distributions: Definitions, Statistical Learning and Applications

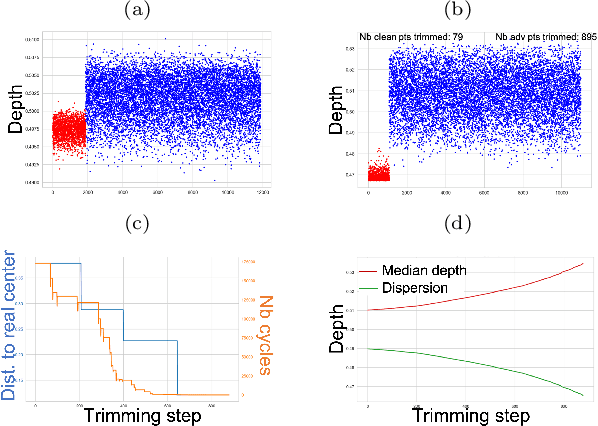
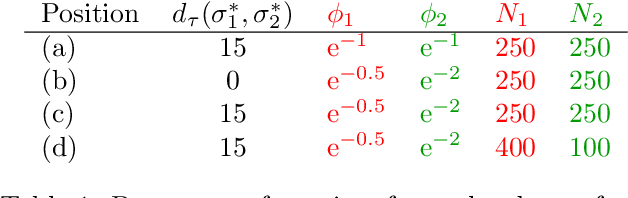
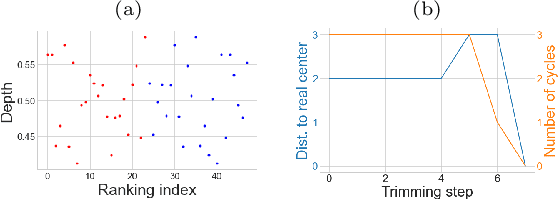
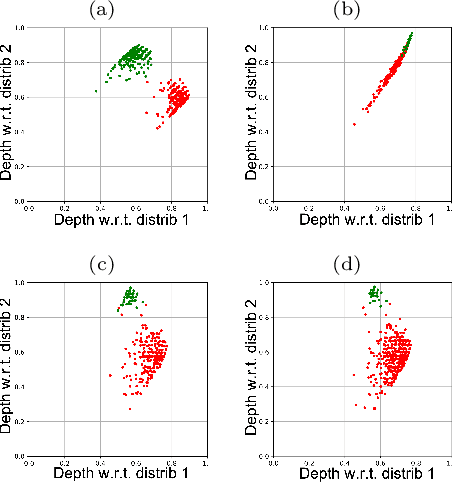
The concept of median/consensus has been widely investigated in order to provide a statistical summary of ranking data, i.e. realizations of a random permutation $\Sigma$ of a finite set, $\{1,\; \ldots,\; n\}$ with $n\geq 1$ say. As it sheds light onto only one aspect of $\Sigma$'s distribution $P$, it may neglect other informative features. It is the purpose of this paper to define analogs of quantiles, ranks and statistical procedures based on such quantities for the analysis of ranking data by means of a metric-based notion of depth function on the symmetric group. Overcoming the absence of vector space structure on $\mathfrak{S}_n$, the latter defines a center-outward ordering of the permutations in the support of $P$ and extends the classic metric-based formulation of consensus ranking (medians corresponding then to the deepest permutations). The axiomatic properties that ranking depths should ideally possess are listed, while computational and generalization issues are studied at length. Beyond the theoretical analysis carried out, the relevance of the novel concepts and methods introduced for a wide variety of statistical tasks are also supported by numerous numerical experiments.

Adversarial Robustness via Adversarial Label-Smoothing

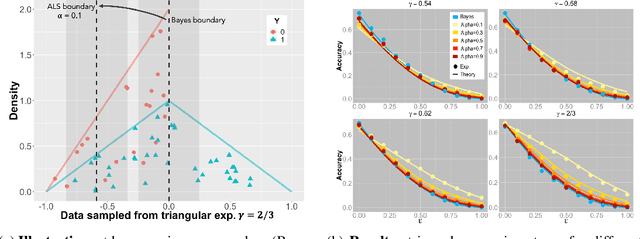
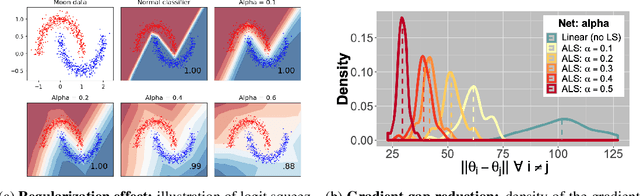
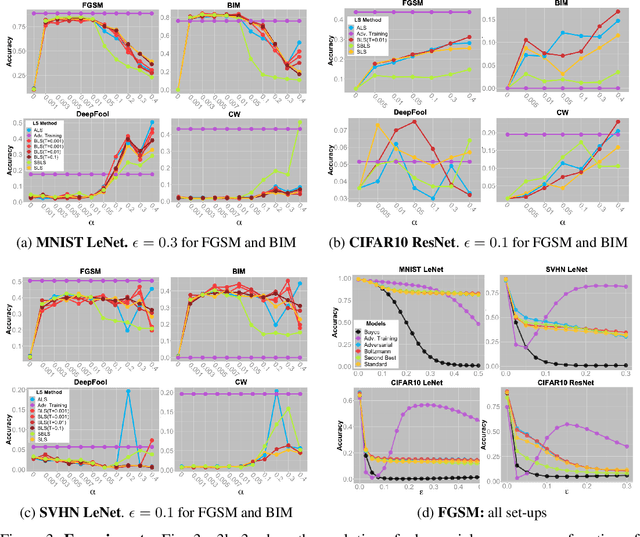
We study Label-Smoothing as a means for improving adversarial robustness of supervised deep-learning models. After establishing a thorough and unified framework, we propose several novel Label-Smoothing methods: adversarial, Boltzmann and second-best Label-Smoothing methods. On various datasets (MNIST, CIFAR10, SVHN) and models (linear models, MLPs, LeNet, ResNet), we show that these methods improve adversarial robustness against a variety of attacks (FGSM, BIM, DeepFool, Carlini-Wagner) by better taking account of the dataset geometry. These proposed Label-Smoothing methods have two main advantages: they can be implemented as a modified cross-entropy loss, thus do not require any modifications of the network architecture nor do they lead to increased training times, and they improve both standard and adversarial accuracy.