Multifidelity data fusion in convolutional encoder/decoder networks

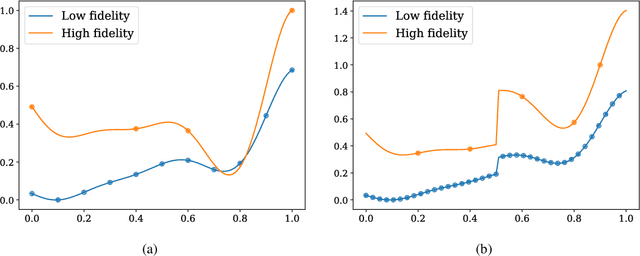
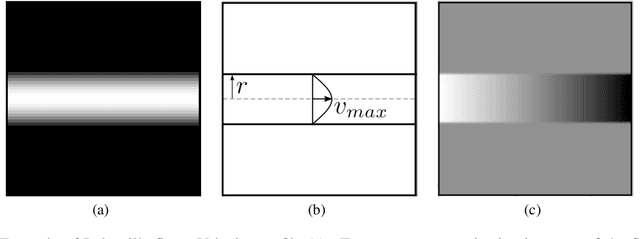
We analyze the regression accuracy of convolutional neural networks assembled from encoders, decoders and skip connections and trained with multifidelity data. Besides requiring significantly less trainable parameters than equivalent fully connected networks, encoder, decoder, encoder-decoder or decoder-encoder architectures can learn the mapping between inputs to outputs of arbitrary dimensionality. We demonstrate their accuracy when trained on a few high-fidelity and many low-fidelity data generated from models ranging from one-dimensional functions to Poisson equation solvers in two-dimensions. We finally discuss a number of implementation choices that improve the reliability of the uncertainty estimates generated by Monte Carlo DropBlocks, and compare uncertainty estimates among low-, high- and multifidelity approaches.