Multifidelity data fusion in convolutional encoder/decoder networks

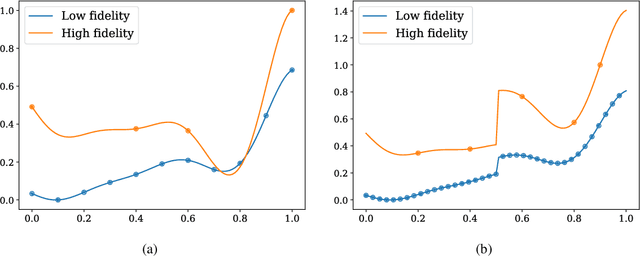
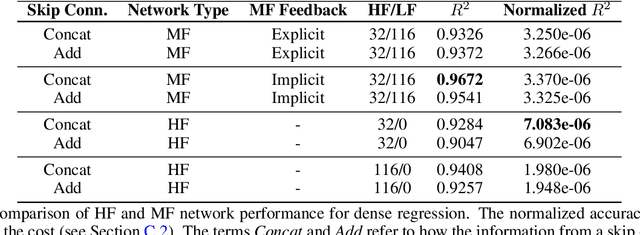
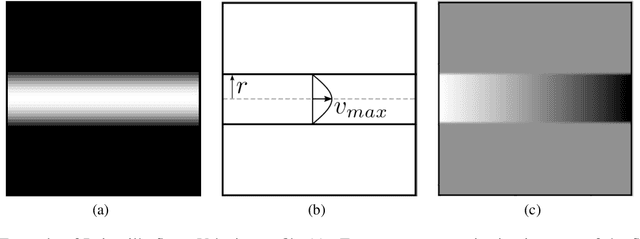
We analyze the regression accuracy of convolutional neural networks assembled from encoders, decoders and skip connections and trained with multifidelity data. Besides requiring significantly less trainable parameters than equivalent fully connected networks, encoder, decoder, encoder-decoder or decoder-encoder architectures can learn the mapping between inputs to outputs of arbitrary dimensionality. We demonstrate their accuracy when trained on a few high-fidelity and many low-fidelity data generated from models ranging from one-dimensional functions to Poisson equation solvers in two-dimensions. We finally discuss a number of implementation choices that improve the reliability of the uncertainty estimates generated by Monte Carlo DropBlocks, and compare uncertainty estimates among low-, high- and multifidelity approaches.

An analysis of reconstruction noise from undersampled 4D flow MRI

Novel Magnetic Resonance (MR) imaging modalities can quantify hemodynamics but require long acquisition times, precluding its widespread use for early diagnosis of cardiovascular disease. To reduce the acquisition times, reconstruction methods from undersampled measurements are routinely used, that leverage representations designed to increase image compressibility. Reconstructed anatomical and hemodynamic images may present visual artifacts. Although some of these artifact are essentially reconstruction errors, and thus a consequence of undersampling, others may be due to measurement noise or the random choice of the sampled frequencies. Said otherwise, a reconstructed image becomes a random variable, and both its bias and its covariance can lead to visual artifacts; the latter leads to spatial correlations that may be misconstrued for visual information. Although the nature of the former has been studied in the literature, the latter has not received as much attention. In this study, we investigate the theoretical properties of the random perturbations arising from the reconstruction process, and perform a number of numerical experiments on simulated and MR aortic flow. Our results show that the correlation length remains limited to two to three pixels when a Gaussian undersampling pattern is combined with recovery algorithms based on $\ell_1$-norm minimization. However, the correlation length may increase significantly for other undersampling patterns, higher undersampling factors (i.e., 8x or 16x compression), and different reconstruction methods.