MFNets: Learning network representations for multifidelity surrogate modeling

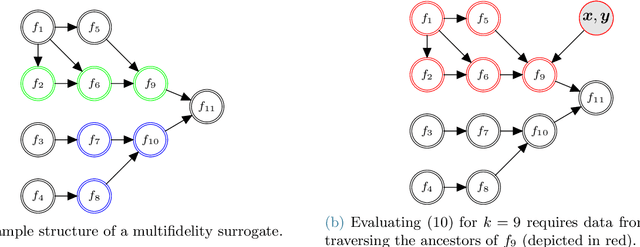
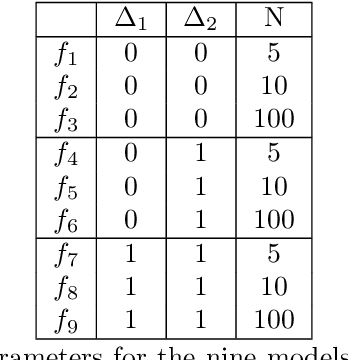
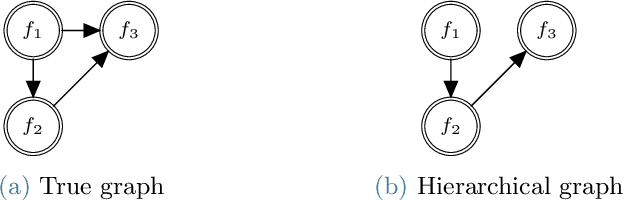
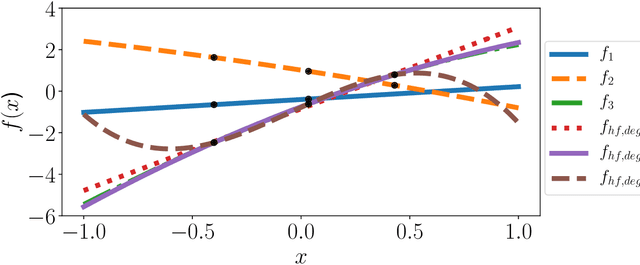
This paper presents an approach for constructing multifidelity surrogate models to simultaneously represent, and learn representations of, multiple information sources. The approach formulates a network of surrogate models whose relationships are defined via localized scalings and shifts. The network can have general structure, and can represent a significantly greater variety of modeling relationships than the hierarchical/recursive networks used in the current state of the art. We show empirically that this flexibility achieves greatest gains in the low-data regime, where the network structure must more efficiently leverage the connections between data sources to yield accurate predictions. We demonstrate our approach on four examples ranging from synthetic to physics-based simulation models. For the numerical test cases adopted here, we obtained an order-of-magnitude reduction in errors compared to multifidelity hierarchical and single-fidelity approaches.