John D. Jakeman
Verification and Validation for Trustworthy Scientific Machine Learning
Feb 21, 2025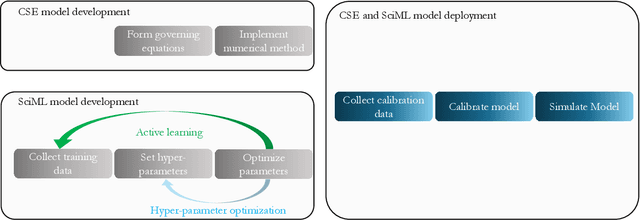
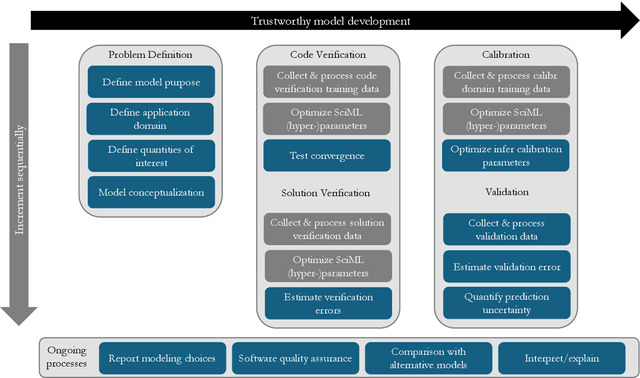
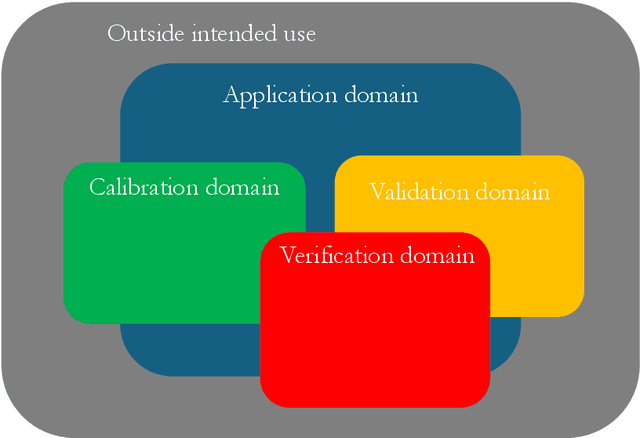
Abstract:Scientific machine learning (SciML) models are transforming many scientific disciplines. However, the development of good modeling practices to increase the trustworthiness of SciML has lagged behind its application, limiting its potential impact. The goal of this paper is to start a discussion on establishing consensus-based good practices for predictive SciML. We identify key challenges in applying existing computational science and engineering guidelines, such as verification and validation protocols, and provide recommendations to address these challenges. Our discussion focuses on predictive SciML, which uses machine learning models to learn, improve, and accelerate numerical simulations of physical systems. While centered on predictive applications, our 16 recommendations aim to help researchers conduc
A switching Kalman filter approach to online mitigation and correction sensor corruption for inertial navigation
Dec 09, 2024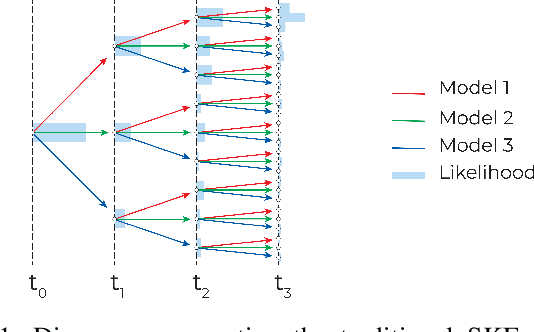
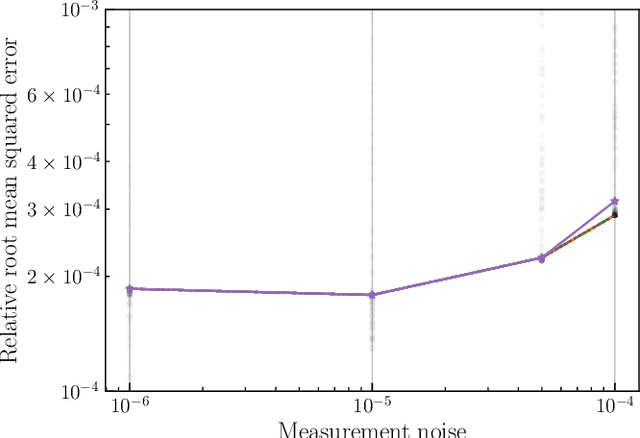
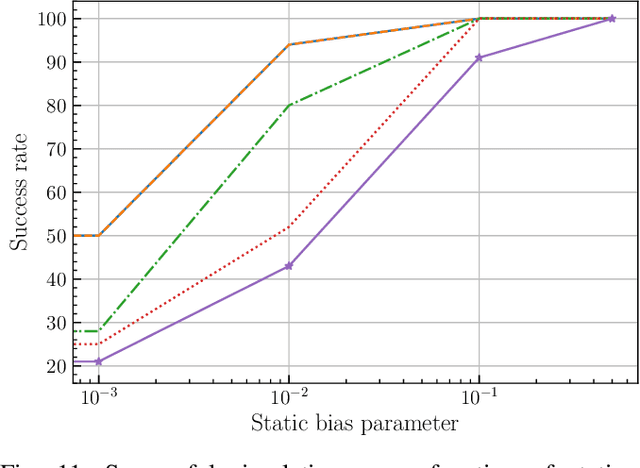
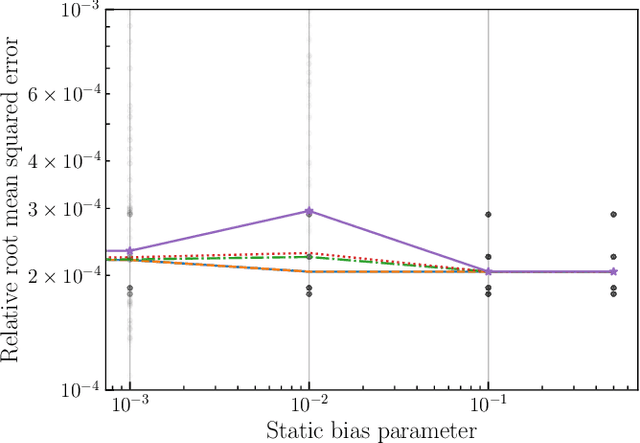
Abstract:This paper introduces a novel approach to detect and address faulty or corrupted external sensors in the context of inertial navigation by leveraging a switching Kalman Filter combined with parameter augmentation. Instead of discarding the corrupted data, the proposed method retains and processes it, running multiple observation models simultaneously and evaluating their likelihoods to accurately identify the true state of the system. We demonstrate the effectiveness of this approach to both identify the moment that a sensor becomes faulty and to correct for the resulting sensor behavior to maintain accurate estimates. We demonstrate our approach on an application of balloon navigation in the atmosphere and shuttle reentry. The results show that our method can accurately recover the true system state even in the presence of significant sensor bias, thereby improving the robustness and reliability of state estimation systems under challenging conditions. We also provide a statistical analysis of problem settings to determine when and where our method is most accurate and where it fails.
Kernel Neural Operators (KNOs) for Scalable, Memory-efficient, Geometrically-flexible Operator Learning
Jun 30, 2024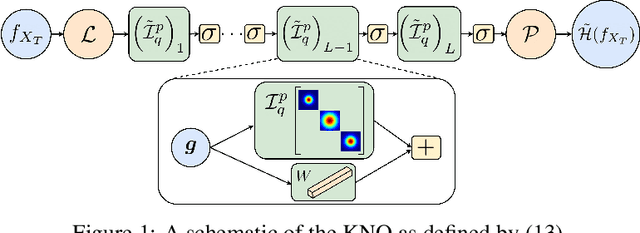
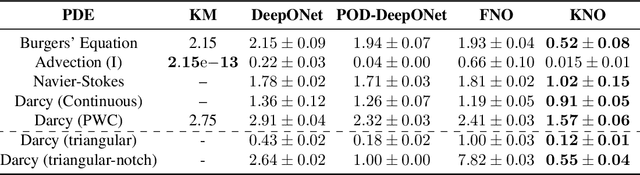
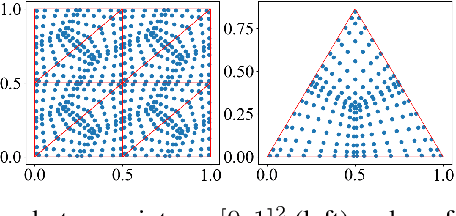
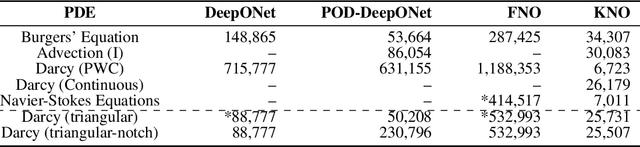
Abstract:This paper introduces the Kernel Neural Operator (KNO), a novel operator learning technique that uses deep kernel-based integral operators in conjunction with quadrature for function-space approximation of operators (maps from functions to functions). KNOs use parameterized, closed-form, finitely-smooth, and compactly-supported kernels with trainable sparsity parameters within the integral operators to significantly reduce the number of parameters that must be learned relative to existing neural operators. Moreover, the use of quadrature for numerical integration endows the KNO with geometric flexibility that enables operator learning on irregular geometries. Numerical results demonstrate that on existing benchmarks the training and test accuracy of KNOs is higher than popular operator learning techniques while using at least an order of magnitude fewer trainable parameters. KNOs thus represent a new paradigm of low-memory, geometrically-flexible, deep operator learning, while retaining the implementation simplicity and transparency of traditional kernel methods from both scientific computing and machine learning.
MFNets: Learning network representations for multifidelity surrogate modeling
Aug 03, 2020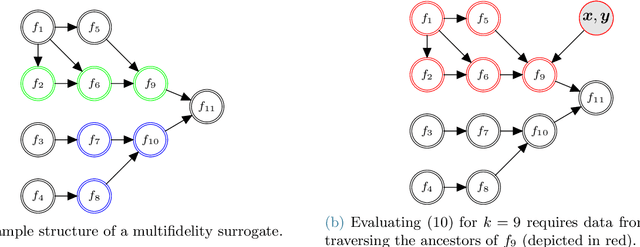
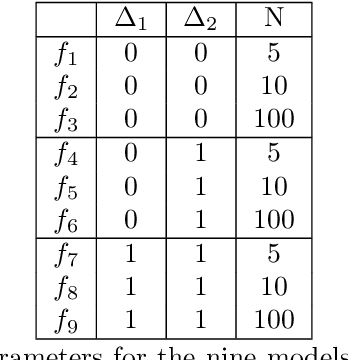
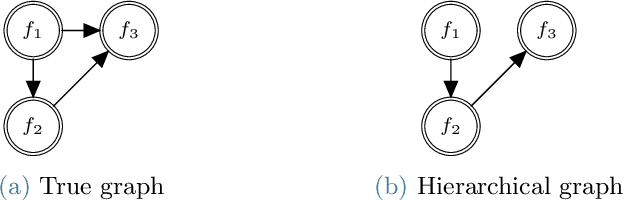
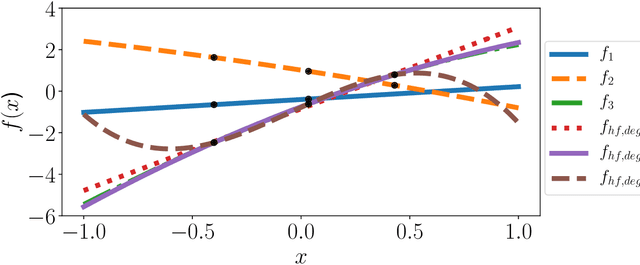
Abstract:This paper presents an approach for constructing multifidelity surrogate models to simultaneously represent, and learn representations of, multiple information sources. The approach formulates a network of surrogate models whose relationships are defined via localized scalings and shifts. The network can have general structure, and can represent a significantly greater variety of modeling relationships than the hierarchical/recursive networks used in the current state of the art. We show empirically that this flexibility achieves greatest gains in the low-data regime, where the network structure must more efficiently leverage the connections between data sources to yield accurate predictions. We demonstrate our approach on four examples ranging from synthetic to physics-based simulation models. For the numerical test cases adopted here, we obtained an order-of-magnitude reduction in errors compared to multifidelity hierarchical and single-fidelity approaches.
Gradient-based Optimization for Regression in the Functional Tensor-Train Format
Jan 11, 2018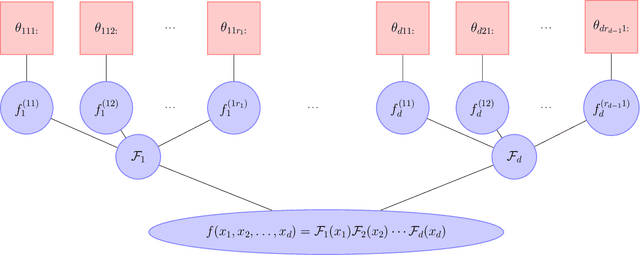


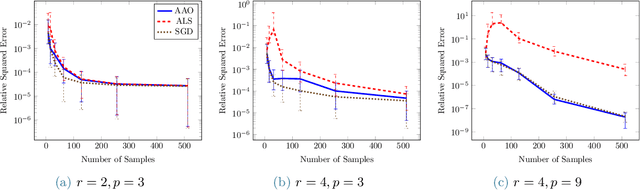
Abstract:We consider the task of low-multilinear-rank functional regression, i.e., learning a low-rank parametric representation of functions from scattered real-valued data. Our first contribution is the development and analysis of an efficient gradient computation that enables gradient-based optimization procedures, including stochastic gradient descent and quasi-Newton methods, for learning the parameters of a functional tensor-train (FT). The functional tensor-train uses the tensor-train (TT) representation of low-rank arrays as an ansatz for a class of low-multilinear-rank functions. The FT is represented by a set of matrix-valued functions that contain a set of univariate functions, and the regression task is to learn the parameters of these univariate functions. Our second contribution demonstrates that using nonlinearly parameterized univariate functions, e.g., symmetric kernels with moving centers, within each core can outperform the standard approach of using a linear expansion of basis functions. Our final contributions are new rank adaptation and group-sparsity regularization procedures to minimize overfitting. We use several benchmark problems to demonstrate at least an order of magnitude lower accuracy with gradient-based optimization methods than standard alternating least squares procedures in the low-sample number regime. We also demonstrate an order of magnitude reduction in accuracy on a test problem resulting from using nonlinear parameterizations over linear parameterizations. Finally we compare regression performance with 22 other nonparametric and parametric regression methods on 10 real-world data sets. We achieve top-five accuracy for seven of the data sets and best accuracy for two of the data sets. These rankings are the best amongst parametric models and competetive with the best non-parametric methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge