Incremental Hierarchical Tucker Decomposition

We present two new algorithms for approximating and updating the hierarchical Tucker decomposition of tensor streams. The first algorithm, Batch Hierarchical Tucker - leaf to root (BHT-l2r), proposes an alternative and more efficient way of approximating a batch of similar tensors in hierarchical Tucker format. The second algorithm, Hierarchical Tucker - Rapid Incremental Subspace Expansion (HT-RISE), updates the batch hierarchical Tucker representation of an accumulated tensor as new batches of tensors become available. The HT-RISE algorithm is suitable for the online setting and never requires full storage or reconstruction of all data while providing a solution to the incremental Tucker decomposition problem. We provide theoretical guarantees for both algorithms and demonstrate their effectiveness on physical and cyber-physical data. The proposed BHT-l2r algorithm and the batch hierarchical Tucker format offers up to $6.2\times$ compression and $3.7\times$ reduction in time over the hierarchical Tucker format. The proposed HT-RISE algorithm also offers up to $3.1\times$ compression and $3.2\times$ reduction in time over a state of the art incremental tensor train decomposition algorithm.

Bayesian Identification of Nonseparable Hamiltonian Systems Using Stochastic Dynamic Models

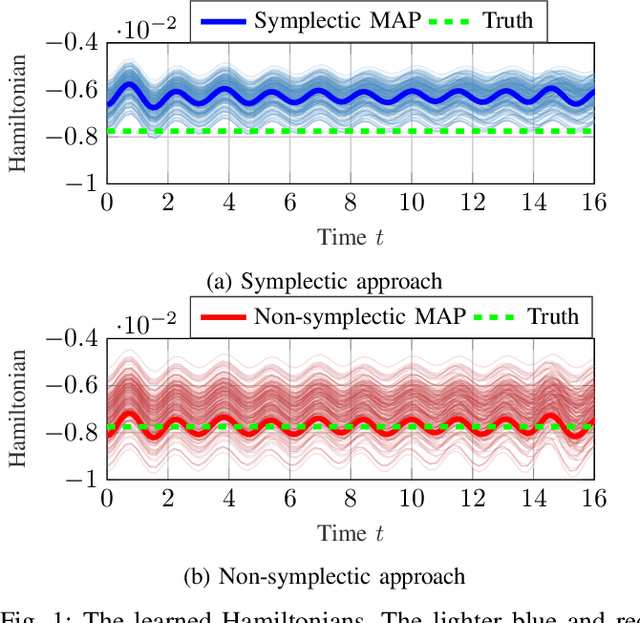
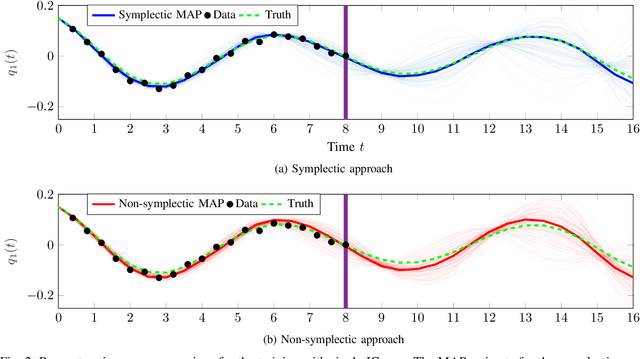
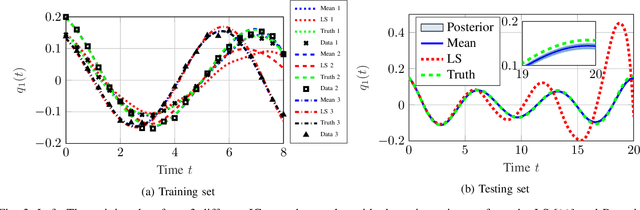
This paper proposes a probabilistic Bayesian formulation for system identification (ID) and estimation of nonseparable Hamiltonian systems using stochastic dynamic models. Nonseparable Hamiltonian systems arise in models from diverse science and engineering applications such as astrophysics, robotics, vortex dynamics, charged particle dynamics, and quantum mechanics. The numerical experiments demonstrate that the proposed method recovers dynamical systems with higher accuracy and reduced predictive uncertainty compared to state-of-the-art approaches. The results further show that accurate predictions far outside the training time interval in the presence of sparse and noisy measurements are possible, which lends robustness and generalizability to the proposed approach. A quantitative benefit is prediction accuracy with less than 10% relative error for more than 12 times longer than a comparable least-squares-based method on a benchmark problem.

High-Dimensional Stochastic Optimal Control using Continuous Tensor Decompositions

Motion planning and control problems are embedded and essential in almost all robotics applications. These problems are often formulated as stochastic optimal control problems and solved using dynamic programming algorithms. Unfortunately, most existing algorithms that guarantee convergence to optimal solutions suffer from the curse of dimensionality: the run time of the algorithm grows exponentially with the dimension of the state space of the system. We propose novel dynamic programming algorithms that alleviate the curse of dimensionality in problems that exhibit certain low-rank structure. The proposed algorithms are based on continuous tensor decompositions recently developed by the authors. Essentially, the algorithms represent high-dimensional functions (e.g., the value function) in a compressed format, and directly perform dynamic programming computations (e.g., value iteration, policy iteration) in this format. Under certain technical assumptions, the new algorithms guarantee convergence towards optimal solutions with arbitrary precision. Furthermore, the run times of the new algorithms scale polynomially with the state dimension and polynomially with the ranks of the value function. This approach realizes substantial computational savings in "compressible" problem instances, where value functions admit low-rank approximations. We demonstrate the new algorithms in a wide range of problems, including a simulated six-dimensional agile quadcopter maneuvering example and a seven-dimensional aircraft perching example. In some of these examples, we estimate computational savings of up to ten orders of magnitude over standard value iteration algorithms. We further demonstrate the algorithms running in real time on board a quadcopter during a flight experiment under motion capture.

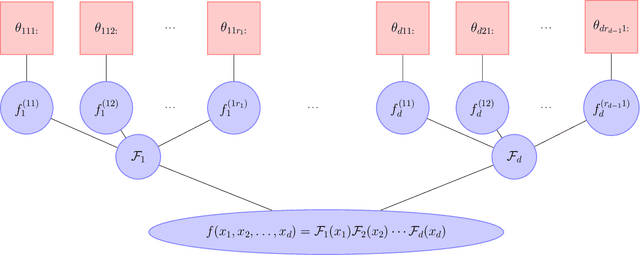
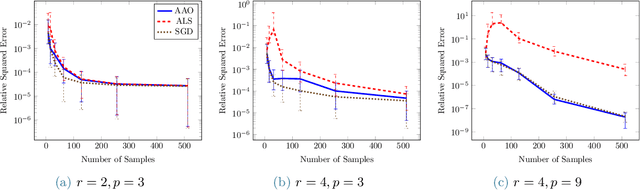
Gradient-based Optimization for Regression in the Functional Tensor-Train Format

We consider the task of low-multilinear-rank functional regression, i.e., learning a low-rank parametric representation of functions from scattered real-valued data. Our first contribution is the development and analysis of an efficient gradient computation that enables gradient-based optimization procedures, including stochastic gradient descent and quasi-Newton methods, for learning the parameters of a functional tensor-train (FT). The functional tensor-train uses the tensor-train (TT) representation of low-rank arrays as an ansatz for a class of low-multilinear-rank functions. The FT is represented by a set of matrix-valued functions that contain a set of univariate functions, and the regression task is to learn the parameters of these univariate functions. Our second contribution demonstrates that using nonlinearly parameterized univariate functions, e.g., symmetric kernels with moving centers, within each core can outperform the standard approach of using a linear expansion of basis functions. Our final contributions are new rank adaptation and group-sparsity regularization procedures to minimize overfitting. We use several benchmark problems to demonstrate at least an order of magnitude lower accuracy with gradient-based optimization methods than standard alternating least squares procedures in the low-sample number regime. We also demonstrate an order of magnitude reduction in accuracy on a test problem resulting from using nonlinear parameterizations over linear parameterizations. Finally we compare regression performance with 22 other nonparametric and parametric regression methods on 10 real-world data sets. We achieve top-five accuracy for seven of the data sets and best accuracy for two of the data sets. These rankings are the best amongst parametric models and competetive with the best non-parametric methods.