NVIDIA Nemotron 3: Efficient and Open Intelligence

We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.

Nemotron 3 Nano: Open, Efficient Mixture-of-Experts Hybrid Mamba-Transformer Model for Agentic Reasoning

We present Nemotron 3 Nano 30B-A3B, a Mixture-of-Experts hybrid Mamba-Transformer language model. Nemotron 3 Nano was pretrained on 25 trillion text tokens, including more than 3 trillion new unique tokens over Nemotron 2, followed by supervised fine tuning and large-scale RL on diverse environments. Nemotron 3 Nano achieves better accuracy than our previous generation Nemotron 2 Nano while activating less than half of the parameters per forward pass. It achieves up to 3.3x higher inference throughput than similarly-sized open models like GPT-OSS-20B and Qwen3-30B-A3B-Thinking-2507, while also being more accurate on popular benchmarks. Nemotron 3 Nano demonstrates enhanced agentic, reasoning, and chat abilities and supports context lengths up to 1M tokens. We release both our pretrained Nemotron 3 Nano 30B-A3B Base and post-trained Nemotron 3 Nano 30B-A3B checkpoints on Hugging Face.

From Facts to Conclusions : Integrating Deductive Reasoning in Retrieval-Augmented LLMs

Retrieval-Augmented Generation (RAG) grounds large language models (LLMs) in external evidence, but fails when retrieved sources conflict or contain outdated or subjective information. Prior work address these issues independently but lack unified reasoning supervision. We propose a reasoning-trace-augmented RAG framework that adds structured, interpretable reasoning across three stages : (1) document-level adjudication, (2) conflict analysis, and (3) grounded synthesis, producing citation-linked answers or justified refusals. A Conflict-Aware Trust-Score (CATS) pipeline is introduced which evaluates groundedness, factual correctness, refusal accuracy, and conflict-behavior alignment using an LLM-as-a-Judge. Our 539-query reasoning dataset and evaluation pipeline establish a foundation for conflict-aware, interpretable RAG systems. Experimental results demonstrate substantial gains over baselines, most notably with Qwen, where Supervised Fine-Tuning improved End-to-End answer correctness from 0.069 to 0.883 and behavioral adherence from 0.074 to 0.722.

Dynamic Shape Control of Soft Robots Enabled by Data-Driven Model Reduction

Soft robots have shown immense promise in settings where they can leverage dynamic control of their entire bodies. However, effective dynamic shape control requires a controller that accounts for the robot's high-dimensional dynamics--a challenge exacerbated by a lack of general-purpose tools for modeling soft robots amenably for control. In this work, we conduct a comparative study of data-driven model reduction techniques for generating linear models amendable to dynamic shape control. We focus on three methods--the eigensystem realization algorithm, dynamic mode decomposition with control, and the Lagrangian operator inference (LOpInf) method. Using each class of model, we explored their efficacy in model predictive control policies for the dynamic shape control of a simulated eel-inspired soft robot in three experiments: 1) tracking simulated reference trajectories guaranteed to be feasible, 2) tracking reference trajectories generated from a biological model of eel kinematics, and 3) tracking reference trajectories generated by a reduced-scale physical analog. In all experiments, the LOpInf-based policies generated lower tracking errors than policies based on other models.

NVIDIA Nemotron Nano 2: An Accurate and Efficient Hybrid Mamba-Transformer Reasoning Model

We introduce Nemotron-Nano-9B-v2, a hybrid Mamba-Transformer language model designed to increase throughput for reasoning workloads while achieving state-of-the-art accuracy compared to similarly-sized models. Nemotron-Nano-9B-v2 builds on the Nemotron-H architecture, in which the majority of the self-attention layers in the common Transformer architecture are replaced with Mamba-2 layers, to achieve improved inference speed when generating the long thinking traces needed for reasoning. We create Nemotron-Nano-9B-v2 by first pre-training a 12-billion-parameter model (Nemotron-Nano-12B-v2-Base) on 20 trillion tokens using an FP8 training recipe. After aligning Nemotron-Nano-12B-v2-Base, we employ the Minitron strategy to compress and distill the model with the goal of enabling inference on up to 128k tokens on a single NVIDIA A10G GPU (22GiB of memory, bfloat16 precision). Compared to existing similarly-sized models (e.g., Qwen3-8B), we show that Nemotron-Nano-9B-v2 achieves on-par or better accuracy on reasoning benchmarks while achieving up to 6x higher inference throughput in reasoning settings like 8k input and 16k output tokens. We are releasing Nemotron-Nano-9B-v2, Nemotron-Nano12B-v2-Base, and Nemotron-Nano-9B-v2-Base checkpoints along with the majority of our pre- and post-training datasets on Hugging Face.

ThematicPlane: Bridging Tacit User Intent and Latent Spaces for Image Generation

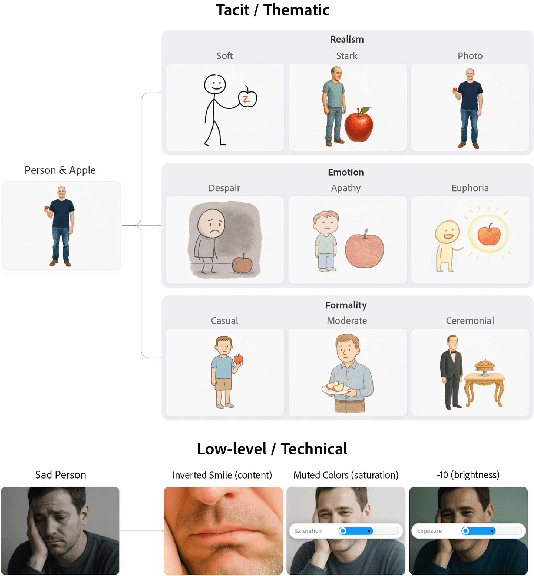
Generative AI has made image creation more accessible, yet aligning outputs with nuanced creative intent remains challenging, particularly for non-experts. Existing tools often require users to externalize ideas through prompts or references, limiting fluid exploration. We introduce ThematicPlane, a system that enables users to navigate and manipulate high-level semantic concepts (e.g., mood, style, or narrative tone) within an interactive thematic design plane. This interface bridges the gap between tacit creative intent and system control. In our exploratory study (N=6), participants engaged in divergent and convergent creative modes, often embracing unexpected results as inspiration or iteration cues. While they grounded their exploration in familiar themes, differing expectations of how themes mapped to outputs revealed a need for more explainable controls. Overall, ThematicPlane fosters expressive, iterative workflows and highlights new directions for intuitive, semantics-driven interaction in generative design tools.

Team ACK at SemEval-2025 Task 2: Beyond Word-for-Word Machine Translation for English-Korean Pairs

Translating knowledge-intensive and entity-rich text between English and Korean requires transcreation to preserve language-specific and cultural nuances beyond literal, phonetic or word-for-word conversion. We evaluate 13 models (LLMs and MT models) using automatic metrics and human assessment by bilingual annotators. Our findings show LLMs outperform traditional MT systems but struggle with entity translation requiring cultural adaptation. By constructing an error taxonomy, we identify incorrect responses and entity name errors as key issues, with performance varying by entity type and popularity level. This work exposes gaps in automatic evaluation metrics and hope to enable future work in completing culturally-nuanced machine translation.

Nonlinear energy-preserving model reduction with lifting transformations that quadratize the energy

Existing model reduction techniques for high-dimensional models of conservative partial differential equations (PDEs) encounter computational bottlenecks when dealing with systems featuring non-polynomial nonlinearities. This work presents a nonlinear model reduction method that employs lifting variable transformations to derive structure-preserving quadratic reduced-order models for conservative PDEs with general nonlinearities. We present an energy-quadratization strategy that defines the auxiliary variable in terms of the nonlinear term in the energy expression to derive an equivalent quadratic lifted system with quadratic system energy. The proposed strategy combined with proper orthogonal decomposition model reduction yields quadratic reduced-order models that conserve the quadratized lifted energy exactly in high dimensions. We demonstrate the proposed model reduction approach on four nonlinear conservative PDEs: the one-dimensional wave equation with exponential nonlinearity, the two-dimensional sine-Gordon equation, the two-dimensional Klein-Gordon equation with parametric dependence, and the two-dimensional Klein-Gordon-Zakharov equations. The numerical results show that the proposed lifting approach is competitive with the state-of-the-art structure-preserving hyper-reduction method in terms of both accuracy and computational efficiency in the online stage while providing significant computational gains in the offline stage.

Data-driven Model Reduction for Soft Robots via Lagrangian Operator Inference

Data-driven model reduction methods provide a nonintrusive way of constructing computationally efficient surrogates of high-fidelity models for real-time control of soft robots. This work leverages the Lagrangian nature of the model equations to derive structure-preserving linear reduced-order models via Lagrangian Operator Inference and compares their performance with prominent linear model reduction techniques through an anguilliform swimming soft robot model example with 231,336 degrees of freedom. The case studies demonstrate that preserving the underlying Lagrangian structure leads to learned models with higher predictive accuracy and robustness to unseen inputs.

Dataflow-Aware PIM-Enabled Manycore Architecture for Deep Learning Workloads

Processing-in-memory (PIM) has emerged as an enabler for the energy-efficient and high-performance acceleration of deep learning (DL) workloads. Resistive random-access memory (ReRAM) is one of the most promising technologies to implement PIM. However, as the complexity of Deep convolutional neural networks (DNNs) grows, we need to design a manycore architecture with multiple ReRAM-based processing elements (PEs) on a single chip. Existing PIM-based architectures mostly focus on computation while ignoring the role of communication. ReRAM-based tiled manycore architectures often involve many Processing Elements (PEs), which need to be interconnected via an efficient on-chip communication infrastructure. Simply allocating more resources (ReRAMs) to speed up only computation is ineffective if the communication infrastructure cannot keep up with it. In this paper, we highlight the design principles of a dataflow-aware PIM-enabled manycore platform tailor-made for various types of DL workloads. We consider the design challenges with both 2.5D interposer- and 3D integration-enabled architectures.