Data-driven identification of latent port-Hamiltonian systems

Conventional physics-based modeling techniques involve high effort, e.g., time and expert knowledge, while data-driven methods often lack interpretability, structure, and sometimes reliability. To mitigate this, we present a data-driven system identification framework that derives models in the port-Hamiltonian (pH) formulation. This formulation is suitable for multi-physical systems while guaranteeing the useful system theoretical properties of passivity and stability. Our framework combines linear and nonlinear reduction with structured, physics-motivated system identification. In this process, high-dimensional state data obtained from possibly nonlinear systems serves as input for an autoencoder, which then performs two tasks: (i) nonlinearly transforming and (ii) reducing this data onto a low-dimensional latent space. In this space, a linear pH system, that satisfies the pH properties per construction, is parameterized by the weights of a neural network. The mathematical requirements are met by defining the pH matrices through Cholesky factorizations. The neural networks that define the coordinate transformation and the pH system are identified in a joint optimization process to match the dynamics observed in the data while defining a linear pH system in the latent space. The learned, low-dimensional pH system can describe even nonlinear systems and is rapidly computable due to its small size. The method is exemplified by a parametric mass-spring-damper and a nonlinear pendulum example, as well as the high-dimensional model of a disc brake with linear thermoelastic behavior.

Symplectic model reduction of Hamiltonian systems using data-driven quadratic manifolds

This work presents two novel approaches for the symplectic model reduction of high-dimensional Hamiltonian systems using data-driven quadratic manifolds. Classical symplectic model reduction approaches employ linear symplectic subspaces for representing the high-dimensional system states in a reduced-dimensional coordinate system. While these approximations respect the symplectic nature of Hamiltonian systems, the linearity of the approximation imposes a fundamental limitation to the accuracy that can be achieved. We propose two different model reduction methods based on recently developed quadratic manifolds, each presenting its own advantages and limitations. The addition of quadratic terms in the state approximation, which sits at the heart of the proposed methodologies, enables us to better represent intrinsic low-dimensionality in the problem at hand. Both approaches are effective for issuing predictions in settings well outside the range of their training data while providing more accurate solutions than the linear symplectic reduced-order models.

Surrogate-data-enriched Physics-Aware Neural Networks

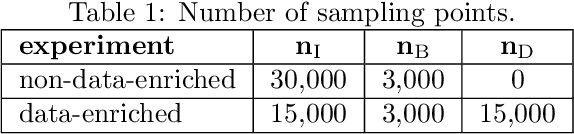
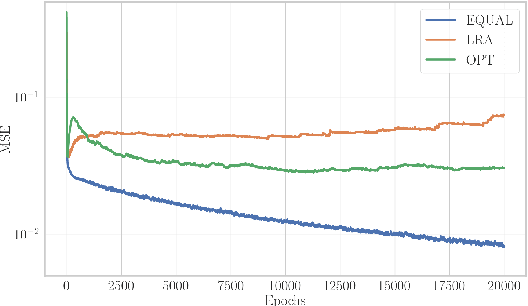
Neural networks can be used as surrogates for PDE models. They can be made physics-aware by penalizing underlying equations or the conservation of physical properties in the loss function during training. Current approaches allow to additionally respect data from numerical simulations or experiments in the training process. However, this data is frequently expensive to obtain and thus only scarcely available for complex models. In this work, we investigate how physics-aware models can be enriched with computationally cheaper, but inexact, data from other surrogate models like Reduced-Order Models (ROMs). In order to avoid trusting too-low-fidelity surrogate solutions, we develop an approach that is sensitive to the error in inexact data. As a proof of concept, we consider the one-dimensional wave equation and show that the training accuracy is increased by two orders of magnitude when inexact data from ROMs is incorporated.