Surrogate-data-enriched Physics-Aware Neural Networks
Paper and Code
Dec 15, 2021
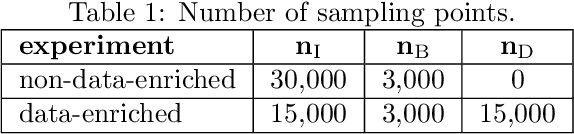

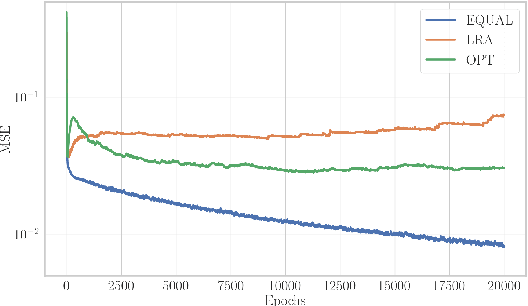
Neural networks can be used as surrogates for PDE models. They can be made physics-aware by penalizing underlying equations or the conservation of physical properties in the loss function during training. Current approaches allow to additionally respect data from numerical simulations or experiments in the training process. However, this data is frequently expensive to obtain and thus only scarcely available for complex models. In this work, we investigate how physics-aware models can be enriched with computationally cheaper, but inexact, data from other surrogate models like Reduced-Order Models (ROMs). In order to avoid trusting too-low-fidelity surrogate solutions, we develop an approach that is sensitive to the error in inexact data. As a proof of concept, we consider the one-dimensional wave equation and show that the training accuracy is increased by two orders of magnitude when inexact data from ROMs is incorporated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge