Large Language Models to Generate System-Level Test Programs Targeting Non-functional Properties

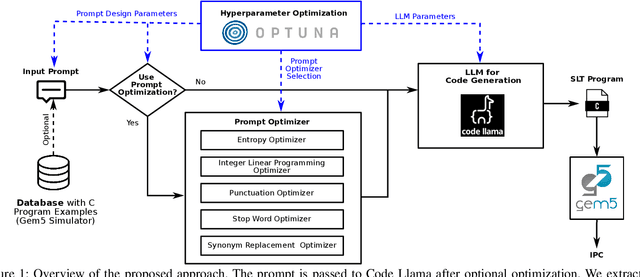
System-Level Test (SLT) has been a part of the test flow for integrated circuits for over a decade and still gains importance. However, no systematic approaches exist for test program generation, especially targeting non-functional properties of the Device under Test (DUT). Currently, test engineers manually compose test suites from off-the-shelf software, approximating the end-user environment of the DUT. This is a challenging and tedious task that does not guarantee sufficient control over non-functional properties. This paper proposes Large Language Models (LLMs) to generate test programs. We take a first glance at how pre-trained LLMs perform in test program generation to optimize non-functional properties of the DUT. Therefore, we write a prompt to generate C code snippets that maximize the instructions per cycle of a super-scalar, out-of-order architecture in simulation. Additionally, we apply prompt and hyperparameter optimization to achieve the best possible results without further training.

Deep learning based surrogate modeling for thermal plume prediction of groundwater heat pumps

The ability for groundwater heat pumps to meet space heating and cooling demands without relying on fossil fuels, has prompted their mass roll out in dense urban environments. In regions with high subsurface groundwater flow rates, the thermal plume generated from a heat pump's injection well can propagate downstream, affecting surrounding users and reducing their heat pump efficiency. To reduce the probability of interference, regulators often rely on simple analytical models or high fidelity groundwater simulations to determine the impact that a heat pump has on the subsurface aquifer and surrounding heat pumps. These are either too inaccurate or too computationally expensive for everyday use. In this work, a surrogate model was developed to provide a quick, high accuracy prediction tool of the thermal plume generated by a heat pump within heterogeneous subsurface aquifers. Three variations of a convolutional neural network were developed that accepts the known groundwater Darcy velocities as discrete two-dimensional inputs and predicts the temperature within the subsurface aquifer around the heat pump. A data set consisting of 800 numerical simulation samples, generated from random permeability fields and pressure boundary conditions, was used to provide pseudo-randomized Darcy velocity fields as input fields and the temperature field solution for training the network. The subsurface temperature field output from the network provides a more realistic temperature field that follows the Darcy velocity streamlines, while being orders of magnitude faster than conventional high fidelity solvers

PDEBENCH: An Extensive Benchmark for Scientific Machine Learning

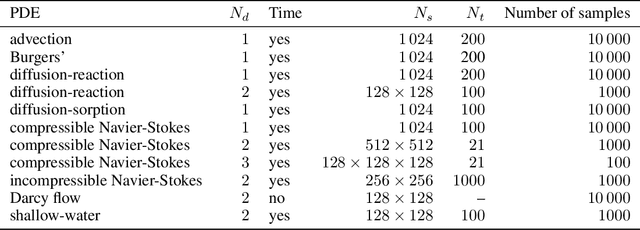
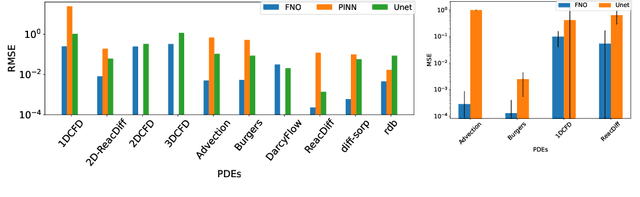
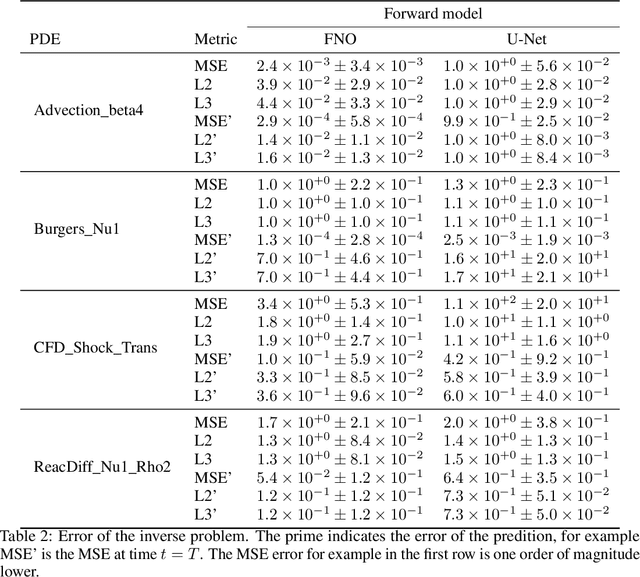
Machine learning-based modeling of physical systems has experienced increased interest in recent years. Despite some impressive progress, there is still a lack of benchmarks for Scientific ML that are easy to use but still challenging and representative of a wide range of problems. We introduce PDEBench, a benchmark suite of time-dependent simulation tasks based on Partial Differential Equations (PDEs). PDEBench comprises both code and data to benchmark the performance of novel machine learning models against both classical numerical simulations and machine learning baselines. Our proposed set of benchmark problems contribute the following unique features: (1) A much wider range of PDEs compared to existing benchmarks, ranging from relatively common examples to more realistic and difficult problems; (2) much larger ready-to-use datasets compared to prior work, comprising multiple simulation runs across a larger number of initial and boundary conditions and PDE parameters; (3) more extensible source codes with user-friendly APIs for data generation and baseline results with popular machine learning models (FNO, U-Net, PINN, Gradient-Based Inverse Method). PDEBench allows researchers to extend the benchmark freely for their own purposes using a standardized API and to compare the performance of new models to existing baseline methods. We also propose new evaluation metrics with the aim to provide a more holistic understanding of learning methods in the context of Scientific ML. With those metrics we identify tasks which are challenging for recent ML methods and propose these tasks as future challenges for the community. The code is available at https://github.com/pdebench/PDEBench.

A Deep Learning Approach for Thermal Plume Prediction of Groundwater Heat Pumps

Climate control of buildings makes up a significant portion of global energy consumption, with groundwater heat pumps providing a suitable alternative. To prevent possibly negative interactions between heat pumps throughout a city, city planners have to optimize their layouts in the future. We develop a novel data-driven approach for building small-scale surrogates for modelling the thermal plumes generated by groundwater heat pumps in the surrounding subsurface water. Building on a data set generated from 2D numerical simulations, we train a convolutional neural network for predicting steady-state subsurface temperature fields from a given subsurface velocity field. We show that compared to existing models ours can capture more complex dynamics while still being quick to compute. The resulting surrogate is thus well-suited for interactive design tools by city planners.

PLSSVM: A (multi-)GPGPU-accelerated Least Squares Support Vector Machine

Machine learning algorithms must be able to efficiently cope with massive data sets. Therefore, they have to scale well on any modern system and be able to exploit the computing power of accelerators independent of their vendor. In the field of supervised learning, Support Vector Machines (SVMs) are widely used. However, even modern and optimized implementations such as LIBSVM or ThunderSVM do not scale well for large non-trivial dense data sets on cutting-edge hardware: Most SVM implementations are based on Sequential Minimal Optimization, an optimized though inherent sequential algorithm. Hence, they are not well-suited for highly parallel GPUs. Furthermore, we are not aware of a performance portable implementation that supports CPUs and GPUs from different vendors. We have developed the PLSSVM library to solve both issues. First, we resort to the formulation of the SVM as a least squares problem. Training an SVM then boils down to solving a system of linear equations for which highly parallel algorithms are known. Second, we provide a hardware independent yet efficient implementation: PLSSVM uses different interchangeable backends--OpenMP, CUDA, OpenCL, SYCL--supporting modern hardware from various vendors like NVIDIA, AMD, or Intel on multiple GPUs. PLSSVM can be used as a drop-in replacement for LIBSVM. We observe a speedup on CPUs of up to 10 compared to LIBSVM and on GPUs of up to 14 compared to ThunderSVM. Our implementation scales on many-core CPUs with a parallel speedup of 74.7 on up to 256 CPU threads and on multiple GPUs with a parallel speedup of 3.71 on four GPUs. The code, utility scripts, and documentation are all available on GitHub: https://github.com/SC-SGS/PLSSVM.

Surrogate-data-enriched Physics-Aware Neural Networks

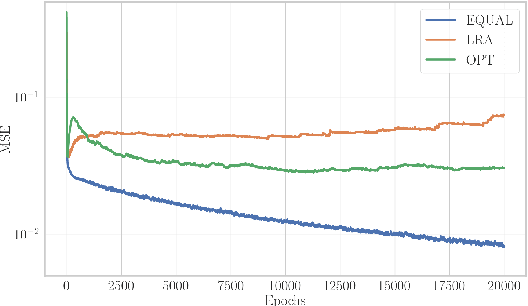
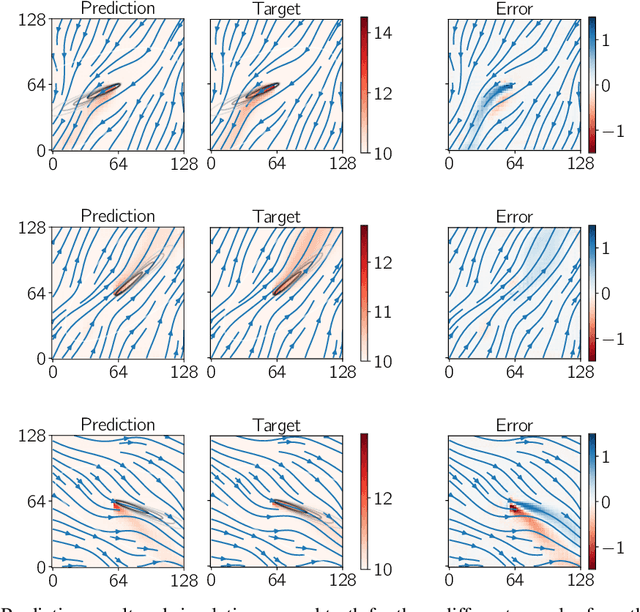
Neural networks can be used as surrogates for PDE models. They can be made physics-aware by penalizing underlying equations or the conservation of physical properties in the loss function during training. Current approaches allow to additionally respect data from numerical simulations or experiments in the training process. However, this data is frequently expensive to obtain and thus only scarcely available for complex models. In this work, we investigate how physics-aware models can be enriched with computationally cheaper, but inexact, data from other surrogate models like Reduced-Order Models (ROMs). In order to avoid trusting too-low-fidelity surrogate solutions, we develop an approach that is sensitive to the error in inexact data. As a proof of concept, we consider the one-dimensional wave equation and show that the training accuracy is increased by two orders of magnitude when inexact data from ROMs is incorporated.

How to Avoid Trivial Solutions in Physics-Informed Neural Networks

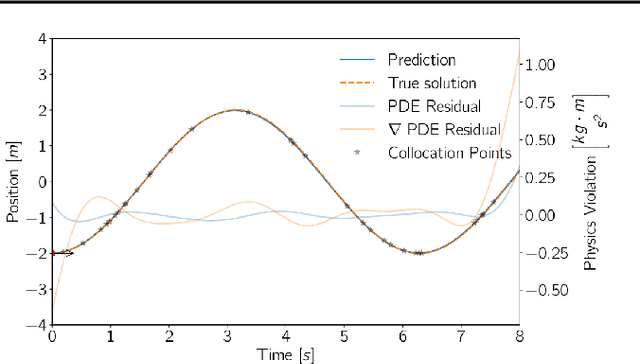
The advent of scientific machine learning (SciML) has opened up a new field with many promises and challenges in the field of simulation science by developing approaches at the interface of physics- and data-based modelling. To this end, physics-informed neural networks (PINNs) have been introduced in recent years, which cope for the scarcity in training data by incorporating physics knowledge of the problem at so-called collocation points. In this work, we investigate the prediction performance of PINNs with respect to the number of collocation points used to enforce the physics-based penalty terms. We show that PINNs can fail, learning a trivial solution that fulfills the physics-derived penalty term by definition. We have developed an alternative sampling approach and a new penalty term enabling us to remedy this core problem of PINNs in data-scarce settings with competitive results while reducing the amount of collocation points needed by up to 80 \% for benchmark problems.

Self-Learning Tuning for Post-Silicon Validation

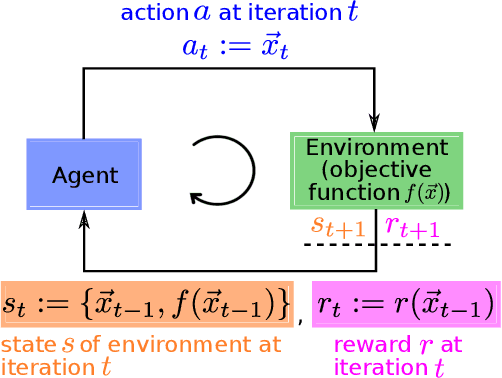
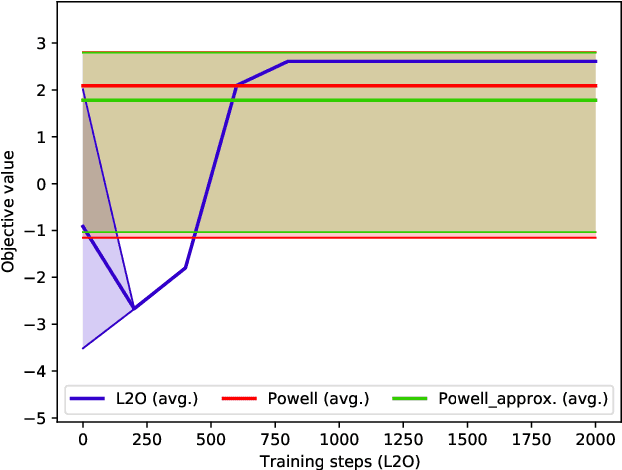
Increasing complexity of modern chips makes design validation more difficult. Existing approaches are not able anymore to cope with the complexity of tasks such as robust performance tuning in post-silicon validation. Therefore, we propose a novel approach based on learn-to-optimize and reinforcement learning in order to solve complex and mixed-type tuning tasks in a efficient and robust way.