Inferring Underwater Topography with FINN

Spatiotemporal partial differential equations (PDEs) find extensive application across various scientific and engineering fields. While numerous models have emerged from both physics and machine learning (ML) communities, there is a growing trend towards integrating these approaches to develop hybrid architectures known as physics-aware machine learning models. Among these, the finite volume neural network (FINN) has emerged as a recent addition. FINN has proven to be particularly efficient in uncovering latent structures in data. In this study, we explore the capabilities of FINN in tackling the shallow-water equations, which simulates wave dynamics in coastal regions. Specifically, we investigate FINN's efficacy to reconstruct underwater topography based on these particular wave equations. Our findings reveal that FINN exhibits a remarkable capacity to infer topography solely from wave dynamics, distinguishing itself from both conventional ML and physics-aware ML models. Our results underscore the potential of FINN in advancing our understanding of spatiotemporal phenomena and enhancing parametrization capabilities in related domains.

The Deep Arbitrary Polynomial Chaos Neural Network or how Deep Artificial Neural Networks could benefit from Data-Driven Homogeneous Chaos Theory

Artificial Intelligence and Machine learning have been widely used in various fields of mathematical computing, physical modeling, computational science, communication science, and stochastic analysis. Approaches based on Deep Artificial Neural Networks (DANN) are very popular in our days. Depending on the learning task, the exact form of DANNs is determined via their multi-layer architecture, activation functions and the so-called loss function. However, for a majority of deep learning approaches based on DANNs, the kernel structure of neural signal processing remains the same, where the node response is encoded as a linear superposition of neural activity, while the non-linearity is triggered by the activation functions. In the current paper, we suggest to analyze the neural signal processing in DANNs from the point of view of homogeneous chaos theory as known from polynomial chaos expansion (PCE). From the PCE perspective, the (linear) response on each node of a DANN could be seen as a $1^{st}$ degree multi-variate polynomial of single neurons from the previous layer, i.e. linear weighted sum of monomials. From this point of view, the conventional DANN structure relies implicitly (but erroneously) on a Gaussian distribution of neural signals. Additionally, this view revels that by design DANNs do not necessarily fulfill any orthogonality or orthonormality condition for a majority of data-driven applications. Therefore, the prevailing handling of neural signals in DANNs could lead to redundant representation as any neural signal could contain some partial information from other neural signals. To tackle that challenge, we suggest to employ the data-driven generalization of PCE theory known as arbitrary polynomial chaos (aPC) to construct a corresponding multi-variate orthonormal representations on each node of a DANN to obtain Deep arbitrary polynomial chaos neural networks.

PDEBENCH: An Extensive Benchmark for Scientific Machine Learning

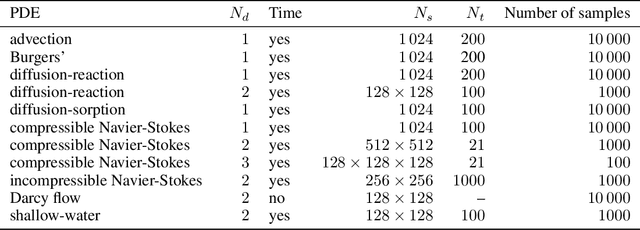
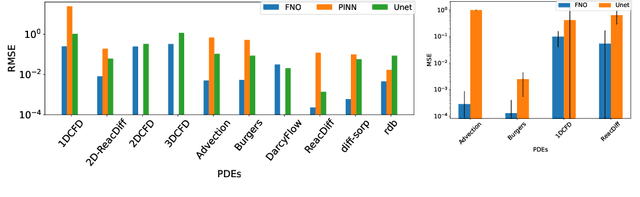
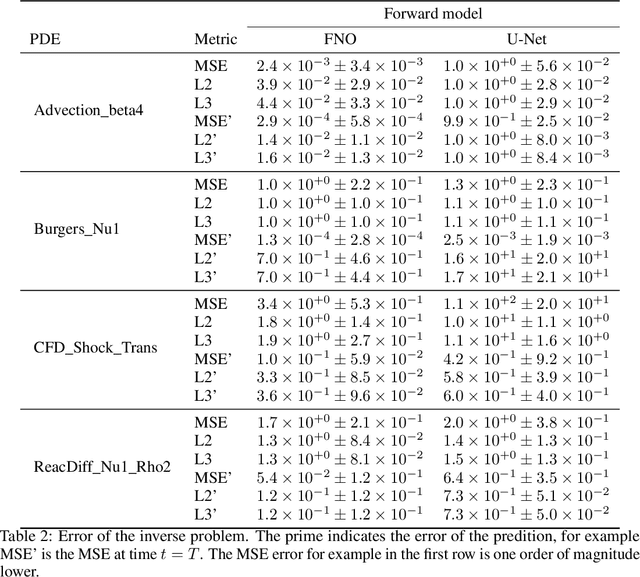
Machine learning-based modeling of physical systems has experienced increased interest in recent years. Despite some impressive progress, there is still a lack of benchmarks for Scientific ML that are easy to use but still challenging and representative of a wide range of problems. We introduce PDEBench, a benchmark suite of time-dependent simulation tasks based on Partial Differential Equations (PDEs). PDEBench comprises both code and data to benchmark the performance of novel machine learning models against both classical numerical simulations and machine learning baselines. Our proposed set of benchmark problems contribute the following unique features: (1) A much wider range of PDEs compared to existing benchmarks, ranging from relatively common examples to more realistic and difficult problems; (2) much larger ready-to-use datasets compared to prior work, comprising multiple simulation runs across a larger number of initial and boundary conditions and PDE parameters; (3) more extensible source codes with user-friendly APIs for data generation and baseline results with popular machine learning models (FNO, U-Net, PINN, Gradient-Based Inverse Method). PDEBench allows researchers to extend the benchmark freely for their own purposes using a standardized API and to compare the performance of new models to existing baseline methods. We also propose new evaluation metrics with the aim to provide a more holistic understanding of learning methods in the context of Scientific ML. With those metrics we identify tasks which are challenging for recent ML methods and propose these tasks as future challenges for the community. The code is available at https://github.com/pdebench/PDEBench.

Composing Partial Differential Equations with Physics-Aware Neural Networks

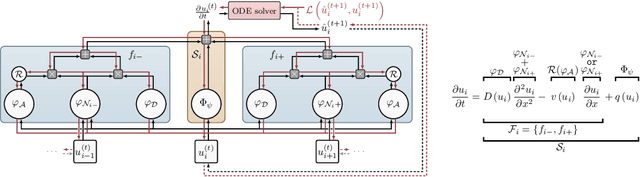
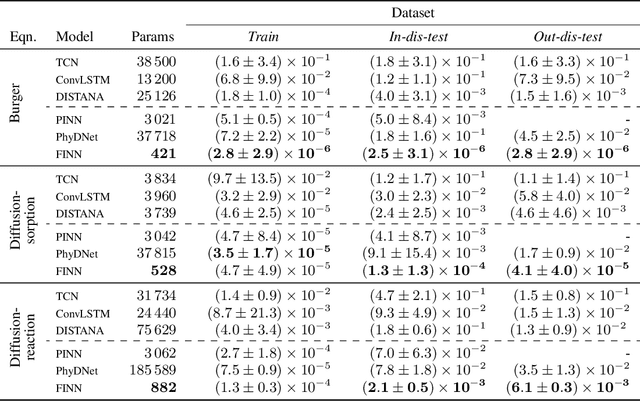
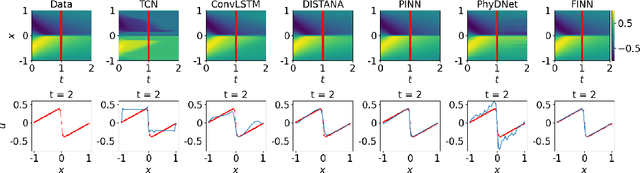
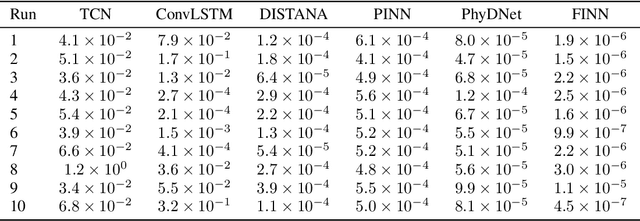
We introduce a compositional physics-aware neural network (FINN) for learning spatiotemporal advection-diffusion processes. FINN implements a new way of combining the learning abilities of artificial neural networks with physical and structural knowledge from numerical simulation by modeling the constituents of partial differential equations (PDEs) in a compositional manner. Results on both one- and two-dimensional PDEs (Burger's, diffusion-sorption, diffusion-reaction, Allen-Cahn) demonstrate FINN's superior modeling accuracy and excellent out-of-distribution generalization ability beyond initial and boundary conditions. With only one tenth of the number of parameters on average, FINN outperforms pure machine learning and other state-of-the-art physics-aware models in all cases -- often even by multiple orders of magnitude. Moreover, FINN outperforms a calibrated physical model when approximating sparse real-world data in a diffusion-sorption scenario, confirming its generalization abilities and showing explanatory potential by revealing the unknown retardation factor of the observed process.

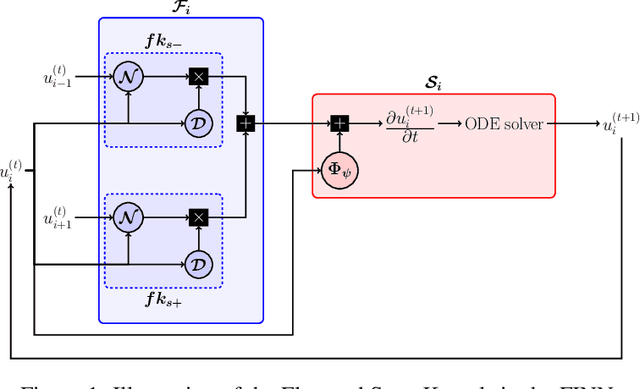
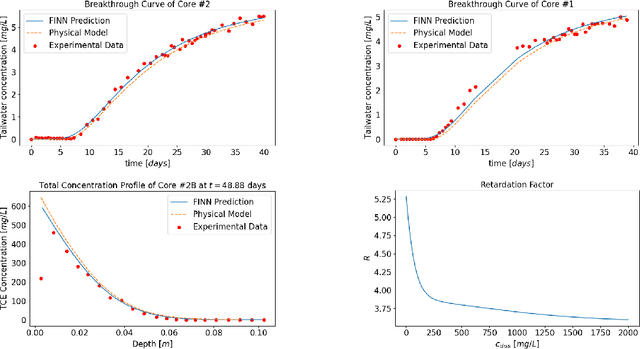
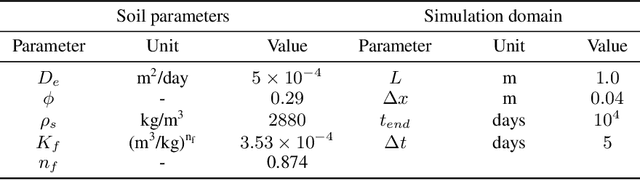
Finite Volume Neural Network: Modeling Subsurface Contaminant Transport

Data-driven modeling of spatiotemporal physical processes with general deep learning methods is a highly challenging task. It is further exacerbated by the limited availability of data, leading to poor generalizations in standard neural network models. To tackle this issue, we introduce a new approach called the Finite Volume Neural Network (FINN). The FINN method adopts the numerical structure of the well-known Finite Volume Method for handling partial differential equations, so that each quantity of interest follows its own adaptable conservation law, while it concurrently accommodates learnable parameters. As a result, FINN enables better handling of fluxes between control volumes and therefore proper treatment of different types of numerical boundary conditions. We demonstrate the effectiveness of our approach with a subsurface contaminant transport problem, which is governed by a non-linear diffusion-sorption process. FINN does not only generalize better to differing boundary conditions compared to other methods, it is also capable to explicitly extract and learn the constitutive relationships (expressed by the retardation factor). More importantly, FINN shows excellent generalization ability when applied to both synthetic datasets and real, sparse experimental data, thus underlining its relevance as a data-driven modeling tool.