Inferring Underwater Topography with FINN

Spatiotemporal partial differential equations (PDEs) find extensive application across various scientific and engineering fields. While numerous models have emerged from both physics and machine learning (ML) communities, there is a growing trend towards integrating these approaches to develop hybrid architectures known as physics-aware machine learning models. Among these, the finite volume neural network (FINN) has emerged as a recent addition. FINN has proven to be particularly efficient in uncovering latent structures in data. In this study, we explore the capabilities of FINN in tackling the shallow-water equations, which simulates wave dynamics in coastal regions. Specifically, we investigate FINN's efficacy to reconstruct underwater topography based on these particular wave equations. Our findings reveal that FINN exhibits a remarkable capacity to infer topography solely from wave dynamics, distinguishing itself from both conventional ML and physics-aware ML models. Our results underscore the potential of FINN in advancing our understanding of spatiotemporal phenomena and enhancing parametrization capabilities in related domains.

The Deep Arbitrary Polynomial Chaos Neural Network or how Deep Artificial Neural Networks could benefit from Data-Driven Homogeneous Chaos Theory

Artificial Intelligence and Machine learning have been widely used in various fields of mathematical computing, physical modeling, computational science, communication science, and stochastic analysis. Approaches based on Deep Artificial Neural Networks (DANN) are very popular in our days. Depending on the learning task, the exact form of DANNs is determined via their multi-layer architecture, activation functions and the so-called loss function. However, for a majority of deep learning approaches based on DANNs, the kernel structure of neural signal processing remains the same, where the node response is encoded as a linear superposition of neural activity, while the non-linearity is triggered by the activation functions. In the current paper, we suggest to analyze the neural signal processing in DANNs from the point of view of homogeneous chaos theory as known from polynomial chaos expansion (PCE). From the PCE perspective, the (linear) response on each node of a DANN could be seen as a $1^{st}$ degree multi-variate polynomial of single neurons from the previous layer, i.e. linear weighted sum of monomials. From this point of view, the conventional DANN structure relies implicitly (but erroneously) on a Gaussian distribution of neural signals. Additionally, this view revels that by design DANNs do not necessarily fulfill any orthogonality or orthonormality condition for a majority of data-driven applications. Therefore, the prevailing handling of neural signals in DANNs could lead to redundant representation as any neural signal could contain some partial information from other neural signals. To tackle that challenge, we suggest to employ the data-driven generalization of PCE theory known as arbitrary polynomial chaos (aPC) to construct a corresponding multi-variate orthonormal representations on each node of a DANN to obtain Deep arbitrary polynomial chaos neural networks.

Probabilistic Regular Tree Priors for Scientific Symbolic Reasoning

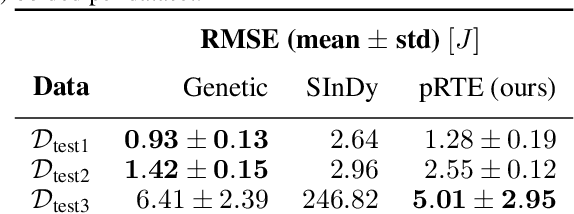
Symbolic Regression (SR) allows for the discovery of scientific equations from data. To limit the large search space of possible equations, prior knowledge has been expressed in terms of formal grammars that characterize subsets of arbitrary strings. However, there is a mismatch between context-free grammars required to express the set of syntactically correct equations, missing closure properties of the former, and a tree structure of the latter. Our contributions are to (i) compactly express experts' prior beliefs about which equations are more likely to be expected by probabilistic Regular Tree Expressions (pRTE), and (ii) adapt Bayesian inference to make such priors efficiently available for symbolic regression encoded as finite state machines. Our scientific case studies show its effectiveness in soil science to find sorption isotherms and for modeling hyper-elastic materials.

The sparse Polynomial Chaos expansion: a fully Bayesian approach with joint priors on the coefficients and global selection of terms

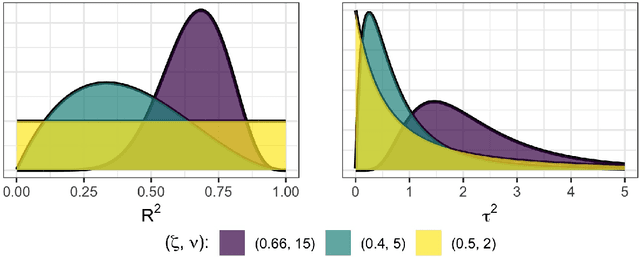
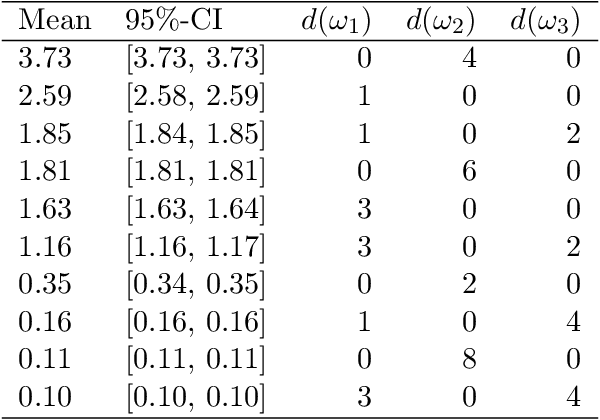
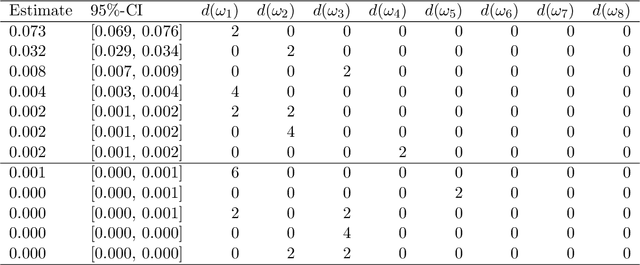
Polynomial chaos expansion (PCE) is a versatile tool widely used in uncertainty quantification and machine learning, but its successful application depends strongly on the accuracy and reliability of the resulting PCE-based response surface. High accuracy typically requires high polynomial degrees, demanding many training points especially in high-dimensional problems through the curse of dimensionality. So-called sparse PCE concepts work with a much smaller selection of basis polynomials compared to conventional PCE approaches and can overcome the curse of dimensionality very efficiently, but have to pay specific attention to their strategies of choosing training points. Furthermore, the approximation error resembles an uncertainty that most existing PCE-based methods do not estimate. In this study, we develop and evaluate a fully Bayesian approach to establish the PCE representation via joint shrinkage priors and Markov chain Monte Carlo. The suggested Bayesian PCE model directly aims to solve the two challenges named above: achieving a sparse PCE representation and estimating uncertainty of the PCE itself. The embedded Bayesian regularizing via the joint shrinkage prior allows using higher polynomial degrees for given training points due to its ability to handle underdetermined situations, where the number of considered PCE coefficients could be much larger than the number of available training points. We also explore multiple variable selection methods to construct sparse PCE expansions based on the established Bayesian representations, while globally selecting the most meaningful orthonormal polynomials given the available training data. We demonstrate the advantages of our Bayesian PCE and the corresponding sparsity-inducing methods on several benchmarks.

Composing Partial Differential Equations with Physics-Aware Neural Networks

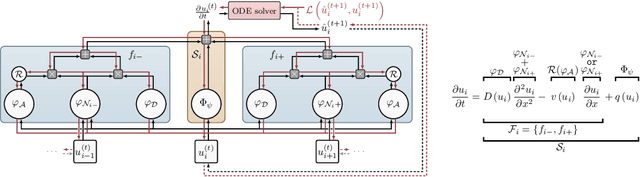
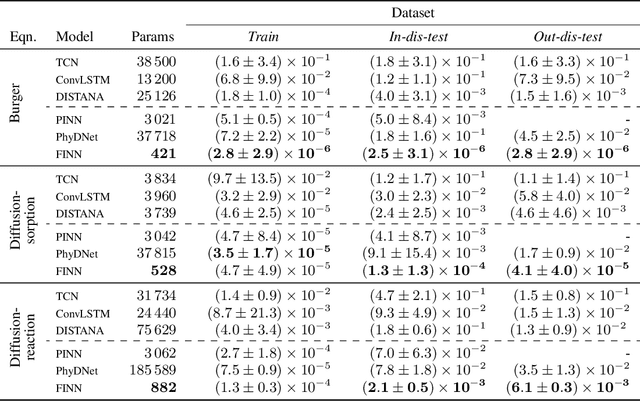
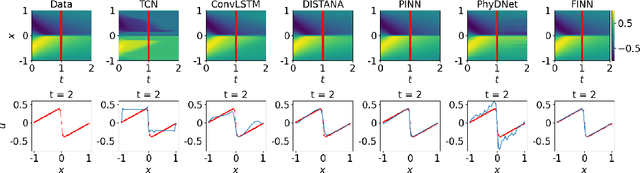
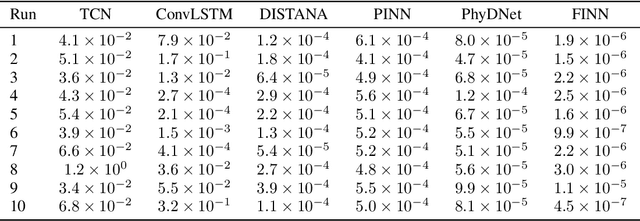
We introduce a compositional physics-aware neural network (FINN) for learning spatiotemporal advection-diffusion processes. FINN implements a new way of combining the learning abilities of artificial neural networks with physical and structural knowledge from numerical simulation by modeling the constituents of partial differential equations (PDEs) in a compositional manner. Results on both one- and two-dimensional PDEs (Burger's, diffusion-sorption, diffusion-reaction, Allen-Cahn) demonstrate FINN's superior modeling accuracy and excellent out-of-distribution generalization ability beyond initial and boundary conditions. With only one tenth of the number of parameters on average, FINN outperforms pure machine learning and other state-of-the-art physics-aware models in all cases -- often even by multiple orders of magnitude. Moreover, FINN outperforms a calibrated physical model when approximating sparse real-world data in a diffusion-sorption scenario, confirming its generalization abilities and showing explanatory potential by revealing the unknown retardation factor of the observed process.

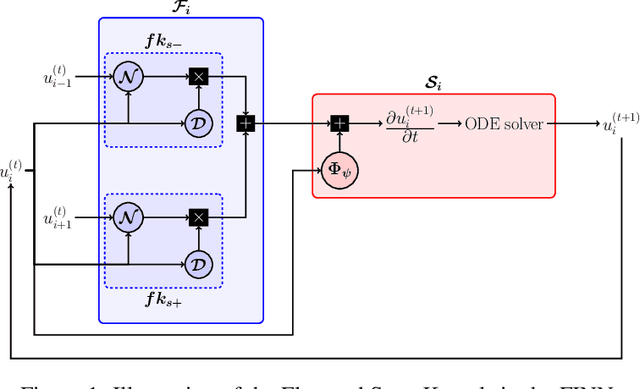
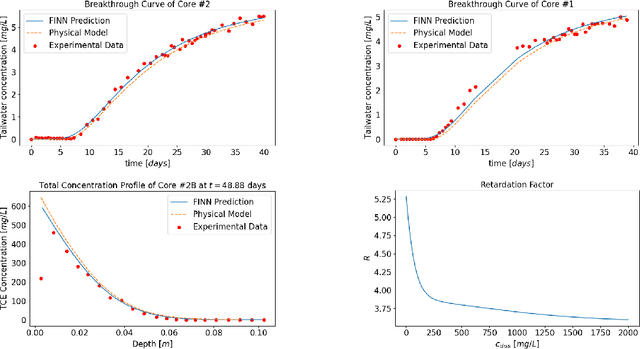
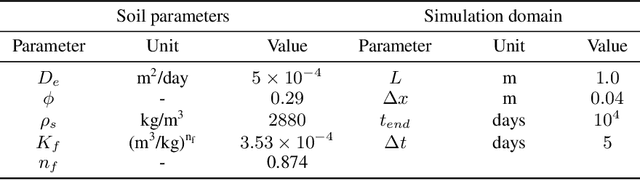
Finite Volume Neural Network: Modeling Subsurface Contaminant Transport

Data-driven modeling of spatiotemporal physical processes with general deep learning methods is a highly challenging task. It is further exacerbated by the limited availability of data, leading to poor generalizations in standard neural network models. To tackle this issue, we introduce a new approach called the Finite Volume Neural Network (FINN). The FINN method adopts the numerical structure of the well-known Finite Volume Method for handling partial differential equations, so that each quantity of interest follows its own adaptable conservation law, while it concurrently accommodates learnable parameters. As a result, FINN enables better handling of fluxes between control volumes and therefore proper treatment of different types of numerical boundary conditions. We demonstrate the effectiveness of our approach with a subsurface contaminant transport problem, which is governed by a non-linear diffusion-sorption process. FINN does not only generalize better to differing boundary conditions compared to other methods, it is also capable to explicitly extract and learn the constitutive relationships (expressed by the retardation factor). More importantly, FINN shows excellent generalization ability when applied to both synthetic datasets and real, sparse experimental data, thus underlining its relevance as a data-driven modeling tool.