Paving the way for scientific foundation models: enhancing generalization and robustness in PDEs with constraint-aware pre-training

Partial differential equations (PDEs) govern a wide range of physical systems, but solving them efficiently remains a major challenge. The idea of a scientific foundation model (SciFM) is emerging as a promising tool for learning transferable representations across diverse domains. However, SciFMs require large amounts of solution data, which may be scarce or computationally expensive to generate. To maximize generalization while reducing data dependence, we propose incorporating PDE residuals into pre-training either as the sole learning signal or in combination with data loss to compensate for limited or infeasible training data. We evaluate this constraint-aware pre-training across three key benchmarks: (i) generalization to new physics, where material properties, e.g., the diffusion coefficient, is shifted with respect to the training distribution; (ii) generalization to entirely new PDEs, requiring adaptation to different operators; and (iii) robustness against noisy fine-tuning data, ensuring stability in real-world applications. Our results show that pre-training with PDE constraints significantly enhances generalization, outperforming models trained solely on solution data across all benchmarks. These findings prove the effectiveness of our proposed constraint-aware pre-training as a crucial component for SciFMs, providing a scalable approach to data-efficient, generalizable PDE solvers.

Probabilistic Regular Tree Priors for Scientific Symbolic Reasoning

Symbolic Regression (SR) allows for the discovery of scientific equations from data. To limit the large search space of possible equations, prior knowledge has been expressed in terms of formal grammars that characterize subsets of arbitrary strings. However, there is a mismatch between context-free grammars required to express the set of syntactically correct equations, missing closure properties of the former, and a tree structure of the latter. Our contributions are to (i) compactly express experts' prior beliefs about which equations are more likely to be expected by probabilistic Regular Tree Expressions (pRTE), and (ii) adapt Bayesian inference to make such priors efficiently available for symbolic regression encoded as finite state machines. Our scientific case studies show its effectiveness in soil science to find sorption isotherms and for modeling hyper-elastic materials.

Partitioned Deep Learning of Fluid-Structure Interaction

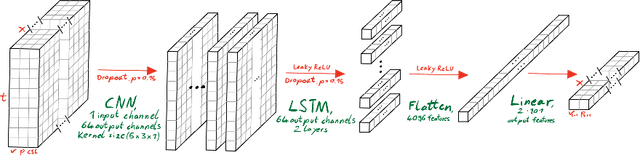
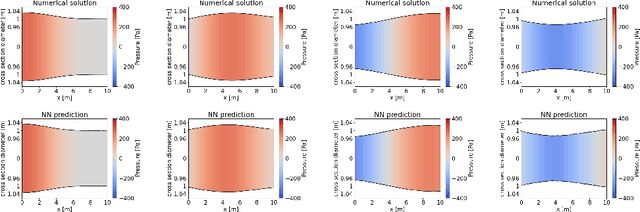
We present a partitioned neural network-based framework for learning of fluid-structure interaction (FSI) problems. We decompose the simulation domain into two smaller sub-domains, i.e., fluid and solid domains, and incorporate an independent neural network for each. A library is used to couple the two networks which takes care of boundary data communication, data mapping and equation coupling. Simulation data are used for training of the both neural networks. We use a combination of convolutional and recurrent neural networks (CNN and RNN) to account for both spatial and temporal connectivity. A quasi-Newton method is used to accelerate the FSI coupling convergence. We observe a very good agreement between the results of the presented framework and the classical numerical methods for simulation of 1d fluid flow inside an elastic tube. This work is a preliminary step for using neural networks to speed-up the FSI coupling convergence by providing an accurate initial guess in each time step for classical numerical solvers