Axel Schumacher
Graph Extraction for Assisting Crash Simulation Data Analysis
Jun 15, 2023Abstract:In this work, we establish a method for abstracting information from Computer Aided Engineering (CAE) into graphs. Such graph representations of CAE data can improve design guidelines and support recommendation systems by enabling the comparison of simulations, highlighting unexplored experimental designs, and correlating different designs. We focus on the load-path in crashworthiness analysis, a complex sub-discipline in vehicle design. The load-path is the sequence of parts that absorb most of the energy caused by the impact. To detect the load-path, we generate a directed weighted graph from the CAE data. The vertices represent the vehicle's parts, and the edges are an abstraction of the connectivity of the parts. The edge direction follows the temporal occurrence of the collision, where the edge weights reflect aspects of the energy absorption. We introduce and assess three methods for graph extraction and an additional method for further updating each graph with the sequences of absorption. Based on longest-path calculations, we introduce an automated detection of the load-path, which we analyse for the different graph extraction methods and weights. Finally, we show how our method for the detection of load-paths helps in the classification and labelling of CAE simulations.
Partitioned Deep Learning of Fluid-Structure Interaction
May 14, 2021

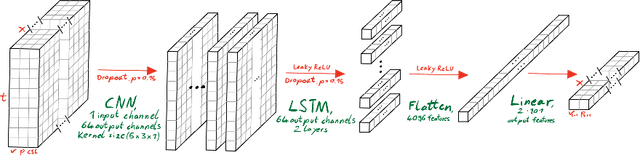
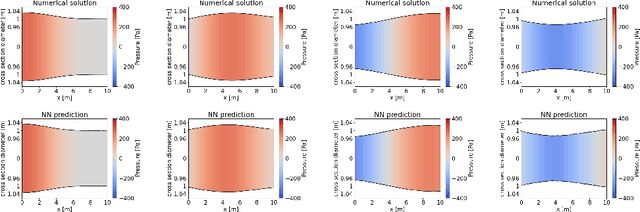
Abstract:We present a partitioned neural network-based framework for learning of fluid-structure interaction (FSI) problems. We decompose the simulation domain into two smaller sub-domains, i.e., fluid and solid domains, and incorporate an independent neural network for each. A library is used to couple the two networks which takes care of boundary data communication, data mapping and equation coupling. Simulation data are used for training of the both neural networks. We use a combination of convolutional and recurrent neural networks (CNN and RNN) to account for both spatial and temporal connectivity. A quasi-Newton method is used to accelerate the FSI coupling convergence. We observe a very good agreement between the results of the presented framework and the classical numerical methods for simulation of 1d fluid flow inside an elastic tube. This work is a preliminary step for using neural networks to speed-up the FSI coupling convergence by providing an accurate initial guess in each time step for classical numerical solvers
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge