Probabilistic Regular Tree Priors for Scientific Symbolic Reasoning
Paper and Code
Jun 14, 2023


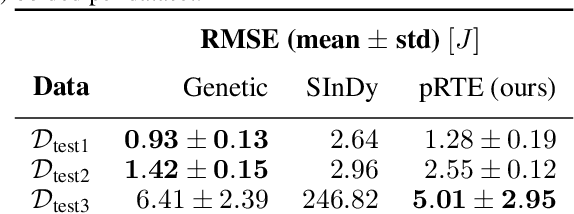
Symbolic Regression (SR) allows for the discovery of scientific equations from data. To limit the large search space of possible equations, prior knowledge has been expressed in terms of formal grammars that characterize subsets of arbitrary strings. However, there is a mismatch between context-free grammars required to express the set of syntactically correct equations, missing closure properties of the former, and a tree structure of the latter. Our contributions are to (i) compactly express experts' prior beliefs about which equations are more likely to be expected by probabilistic Regular Tree Expressions (pRTE), and (ii) adapt Bayesian inference to make such priors efficiently available for symbolic regression encoded as finite state machines. Our scientific case studies show its effectiveness in soil science to find sorption isotherms and for modeling hyper-elastic materials.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge