Paving the way for scientific foundation models: enhancing generalization and robustness in PDEs with constraint-aware pre-training

Partial differential equations (PDEs) govern a wide range of physical systems, but solving them efficiently remains a major challenge. The idea of a scientific foundation model (SciFM) is emerging as a promising tool for learning transferable representations across diverse domains. However, SciFMs require large amounts of solution data, which may be scarce or computationally expensive to generate. To maximize generalization while reducing data dependence, we propose incorporating PDE residuals into pre-training either as the sole learning signal or in combination with data loss to compensate for limited or infeasible training data. We evaluate this constraint-aware pre-training across three key benchmarks: (i) generalization to new physics, where material properties, e.g., the diffusion coefficient, is shifted with respect to the training distribution; (ii) generalization to entirely new PDEs, requiring adaptation to different operators; and (iii) robustness against noisy fine-tuning data, ensuring stability in real-world applications. Our results show that pre-training with PDE constraints significantly enhances generalization, outperforming models trained solely on solution data across all benchmarks. These findings prove the effectiveness of our proposed constraint-aware pre-training as a crucial component for SciFMs, providing a scalable approach to data-efficient, generalizable PDE solvers.

Effects of Pre- and Post-Processing on type-based Embeddings in Lexical Semantic Change Detection

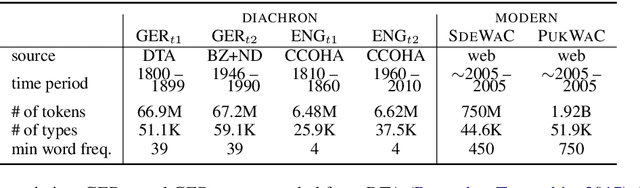
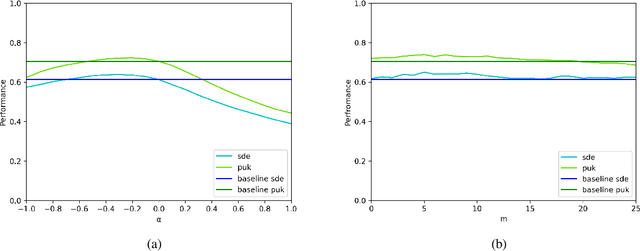
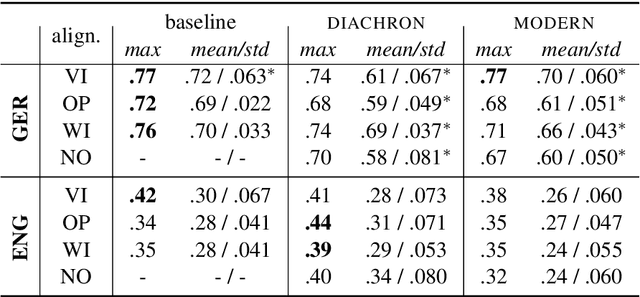
Lexical semantic change detection is a new and innovative research field. The optimal fine-tuning of models including pre- and post-processing is largely unclear. We optimize existing models by (i) pre-training on large corpora and refining on diachronic target corpora tackling the notorious small data problem, and (ii) applying post-processing transformations that have been shown to improve performance on synchronic tasks. Our results provide a guide for the application and optimization of lexical semantic change detection models across various learning scenarios.