Inferring Underwater Topography with FINN

Spatiotemporal partial differential equations (PDEs) find extensive application across various scientific and engineering fields. While numerous models have emerged from both physics and machine learning (ML) communities, there is a growing trend towards integrating these approaches to develop hybrid architectures known as physics-aware machine learning models. Among these, the finite volume neural network (FINN) has emerged as a recent addition. FINN has proven to be particularly efficient in uncovering latent structures in data. In this study, we explore the capabilities of FINN in tackling the shallow-water equations, which simulates wave dynamics in coastal regions. Specifically, we investigate FINN's efficacy to reconstruct underwater topography based on these particular wave equations. Our findings reveal that FINN exhibits a remarkable capacity to infer topography solely from wave dynamics, distinguishing itself from both conventional ML and physics-aware ML models. Our results underscore the potential of FINN in advancing our understanding of spatiotemporal phenomena and enhancing parametrization capabilities in related domains.

Comparing and Contrasting Deep Learning Weather Prediction Backbones on Navier-Stokes and Atmospheric Dynamics

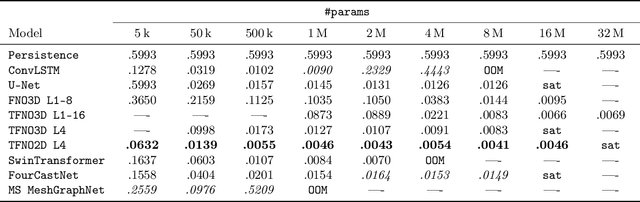
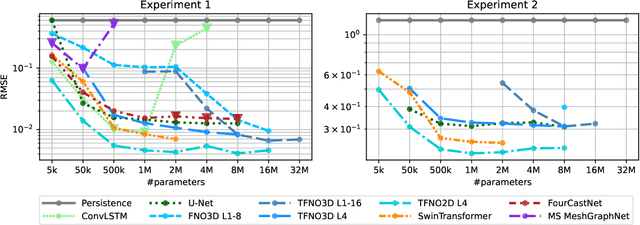
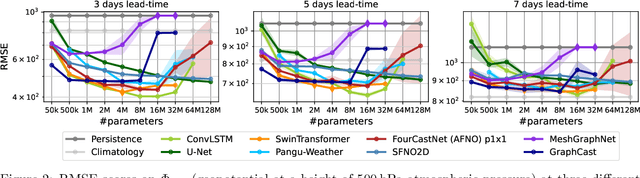
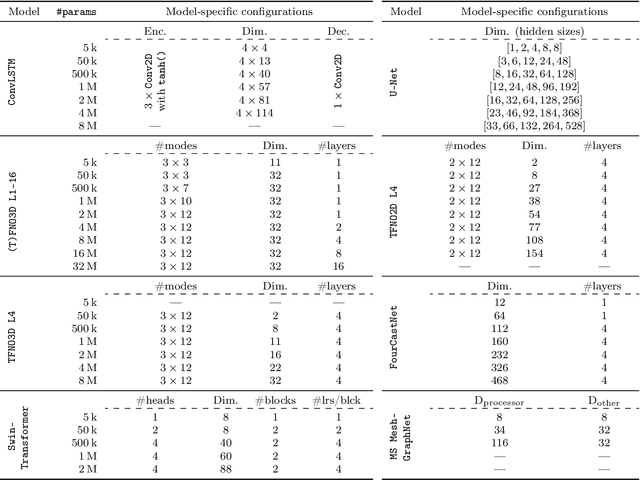
Remarkable progress in the development of Deep Learning Weather Prediction (DLWP) models positions them to become competitive with traditional numerical weather prediction (NWP) models. Indeed, a wide number of DLWP architectures -- based on various backbones, including U-Net, Transformer, Graph Neural Network (GNN), and Fourier Neural Operator (FNO) -- have demonstrated their potential at forecasting atmospheric states. However, due to differences in training protocols, forecast horizons, and data choices, it remains unclear which (if any) of these methods and architectures are most suitable for weather forecasting and for future model development. Here, we step back and provide a detailed empirical analysis, under controlled conditions, comparing and contrasting the most prominent DLWP models, along with their backbones. We accomplish this by predicting synthetic two-dimensional incompressible Navier-Stokes and real-world global weather dynamics. In terms of accuracy, memory consumption, and runtime, our results illustrate various tradeoffs. For example, on synthetic data, we observe favorable performance of FNO; and on the real-world WeatherBench dataset, our results demonstrate the suitability of ConvLSTM and SwinTransformer for short-to-mid-ranged forecasts. For long-ranged weather rollouts of up to 365 days, we observe superior stability and physical soundness in architectures that formulate a spherical data representation, i.e., GraphCast and Spherical FNO. In addition, we observe that all of these model backbones ``saturate,'' i.e., none of them exhibit so-called neural scaling, which highlights an important direction for future work on these and related models.

Inductive biases in deep learning models for weather prediction

Deep learning has recently gained immense popularity in the Earth sciences as it enables us to formulate purely data-driven models of complex Earth system processes. Deep learning-based weather prediction (DLWP) models have made significant progress in the last few years, achieving forecast skills comparable to established numerical weather prediction (NWP) models with comparatively lesser computational costs. In order to train accurate, reliable, and tractable DLWP models with several millions of parameters, the model design needs to incorporate suitable inductive biases that encode structural assumptions about the data and modelled processes. When chosen appropriately, these biases enable faster learning and better generalisation to unseen data. Although inductive biases play a crucial role in successful DLWP models, they are often not stated explicitly and how they contribute to model performance remains unclear. Here, we review and analyse the inductive biases of six state-of-the-art DLWP models, involving a deeper look at five key design elements: input data, forecasting objective, loss components, layered design of the deep learning architectures, and optimisation methods. We show how the design choices made in each of the five design elements relate to structural assumptions. Given recent developments in the broader DL community, we anticipate that the future of DLWP will likely see a wider use of foundation models -- large models pre-trained on big databases with self-supervised learning -- combined with explicit physics-informed inductive biases that allow the models to provide competitive forecasts even at the more challenging subseasonal-to-seasonal scales.

Learning What and Where -- Unsupervised Disentangling Location and Identity Tracking

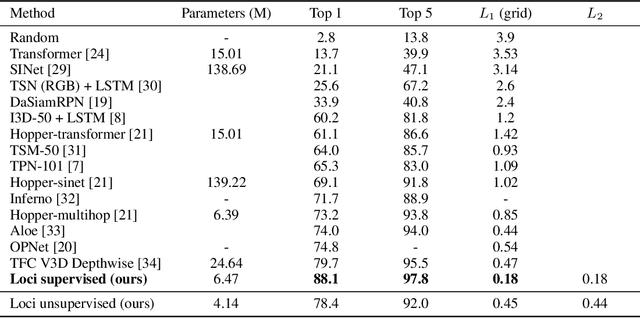
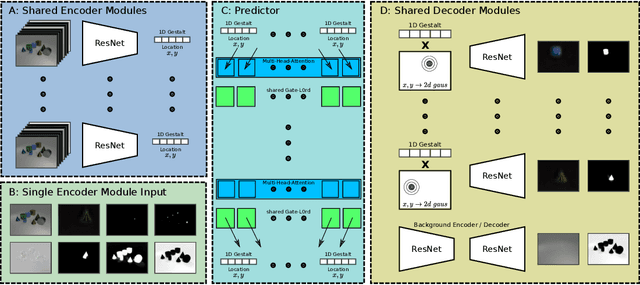
Our brain can almost effortlessly decompose visual data streams into background and salient objects. Moreover, it can track the objects and anticipate their motion and interactions. In contrast, recent object reasoning datasets, such as CATER, have revealed fundamental shortcomings of current vision-based AI systems, particularly when targeting explicit object encodings, object permanence, and object reasoning. We introduce an unsupervised disentangled LOCation and Identity tracking system (Loci), which excels on the CATER tracking challenge. Inspired by the dorsal-ventral pathways in the brain, Loci tackles the what-and-where binding problem by means of a self-supervised segregation mechanism. Our autoregressive neural network partitions and distributes the visual input stream across separate, identically-parameterized and autonomously recruited neural network modules. Each module binds what with where, that is, compressed Gestalt encodings with locations. On the deep latent encoding levels interaction dynamics are processed. Besides exhibiting superior performance in current benchmarks, we propose that Loci may set the stage for deeper, explanation-oriented video processing -- akin to some deeper networked processes in the brain that appear to integrate individual entity and spatiotemporal interaction dynamics into event structures.

Composing Partial Differential Equations with Physics-Aware Neural Networks

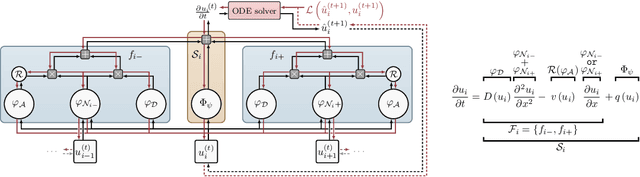
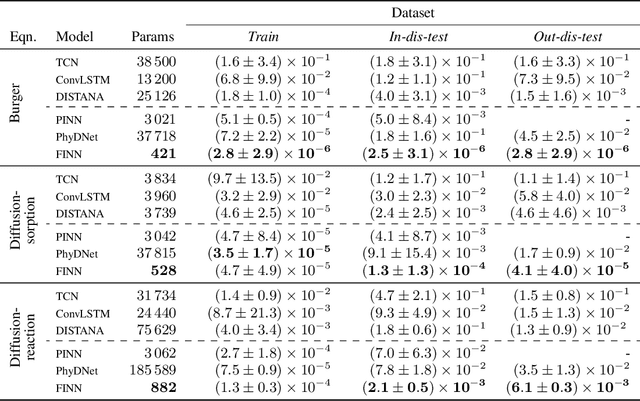
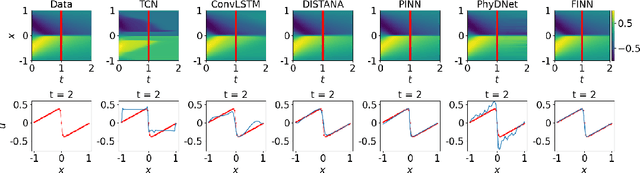
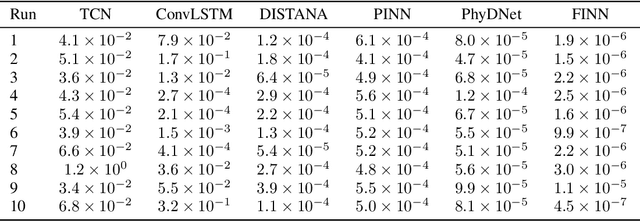
We introduce a compositional physics-aware neural network (FINN) for learning spatiotemporal advection-diffusion processes. FINN implements a new way of combining the learning abilities of artificial neural networks with physical and structural knowledge from numerical simulation by modeling the constituents of partial differential equations (PDEs) in a compositional manner. Results on both one- and two-dimensional PDEs (Burger's, diffusion-sorption, diffusion-reaction, Allen-Cahn) demonstrate FINN's superior modeling accuracy and excellent out-of-distribution generalization ability beyond initial and boundary conditions. With only one tenth of the number of parameters on average, FINN outperforms pure machine learning and other state-of-the-art physics-aware models in all cases -- often even by multiple orders of magnitude. Moreover, FINN outperforms a calibrated physical model when approximating sparse real-world data in a diffusion-sorption scenario, confirming its generalization abilities and showing explanatory potential by revealing the unknown retardation factor of the observed process.

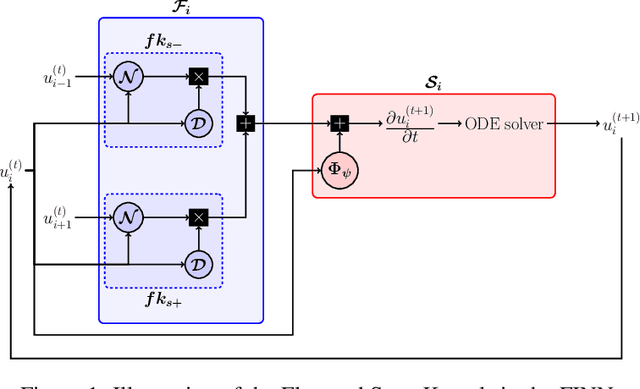
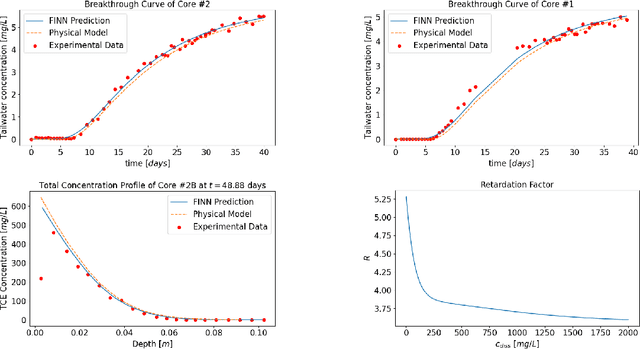
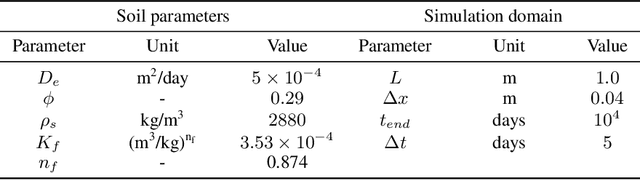
Finite Volume Neural Network: Modeling Subsurface Contaminant Transport

Data-driven modeling of spatiotemporal physical processes with general deep learning methods is a highly challenging task. It is further exacerbated by the limited availability of data, leading to poor generalizations in standard neural network models. To tackle this issue, we introduce a new approach called the Finite Volume Neural Network (FINN). The FINN method adopts the numerical structure of the well-known Finite Volume Method for handling partial differential equations, so that each quantity of interest follows its own adaptable conservation law, while it concurrently accommodates learnable parameters. As a result, FINN enables better handling of fluxes between control volumes and therefore proper treatment of different types of numerical boundary conditions. We demonstrate the effectiveness of our approach with a subsurface contaminant transport problem, which is governed by a non-linear diffusion-sorption process. FINN does not only generalize better to differing boundary conditions compared to other methods, it is also capable to explicitly extract and learn the constitutive relationships (expressed by the retardation factor). More importantly, FINN shows excellent generalization ability when applied to both synthetic datasets and real, sparse experimental data, thus underlining its relevance as a data-driven modeling tool.

Active Tuning

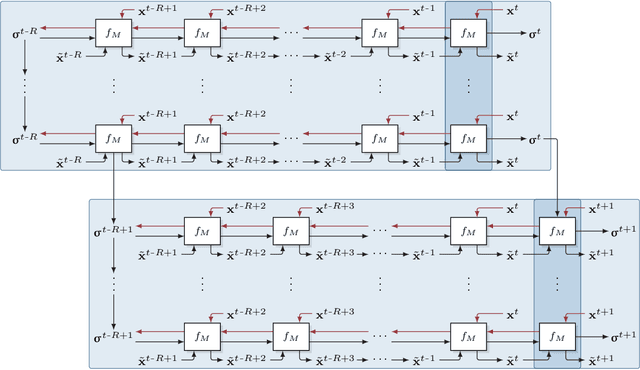
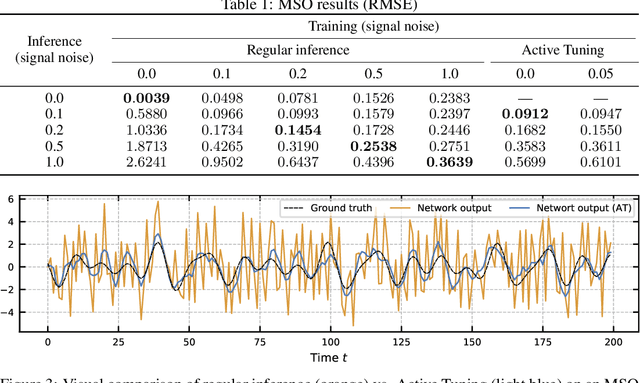
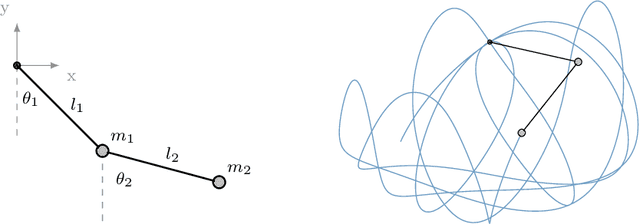
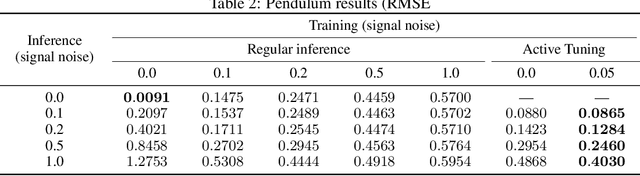
We introduce Active Tuning, a novel paradigm for optimizing the internal dynamics of recurrent neural networks (RNNs) on the fly. In contrast to the conventional sequence-to-sequence mapping scheme, Active Tuning decouples the RNN's recurrent neural activities from the input stream, using the unfolding temporal gradient signal to tune the internal dynamics into the data stream. As a consequence, the model output depends only on its internal hidden dynamics and the closed-loop feedback of its own predictions; its hidden state is continuously adapted by means of the temporal gradient resulting from backpropagating the discrepancy between the signal observations and the model outputs through time. In this way, Active Tuning infers the signal actively but indirectly based on the originally learned temporal patterns, fitting the most plausible hidden state sequence into the observations. We demonstrate the effectiveness of Active Tuning on several time series denoising benchmarks, including multiple super-imposed sine waves, a chaotic double pendulum, and spatiotemporal wave dynamics. Active Tuning consistently improves the robustness, accuracy, and generalization abilities of all evaluated models. Moreover, networks trained for signal prediction and denoising can be successfully applied to a much larger range of noise conditions with the help of Active Tuning. Thus, given a capable time series predictor, Active Tuning enhances its online signal filtering, denoising, and reconstruction abilities without the need for additional training.

Hidden Latent State Inference in a Spatio-Temporal Generative Model

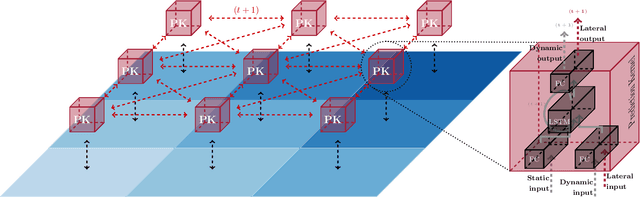
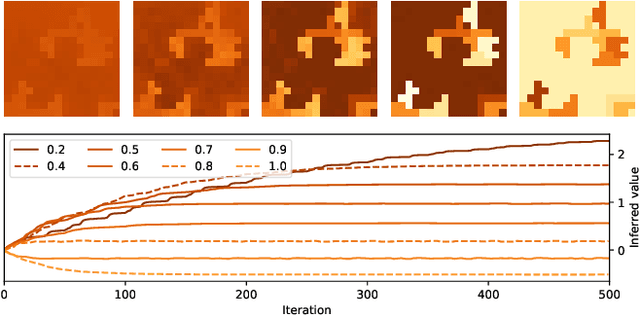
Knowledge of the hidden factors that determine particular system dynamics is crucial for both explaining them and pursuing goal-directed, interventional actions. The inference of these factors without supervision given time series data remains an open challenge. Here, we focus on spatio-temporal processes, including wave propagations and weather dynamics, and assume that universal causes (e.g. physics) apply throughout space and time. We apply a novel DIstributed, Spatio-Temporal graph Artificial Neural network Architecture, DISTANA, which learns a generative model in such domains. DISTANA requires fewer parameters, and yields more accurate predictions than temporal convolutional neural networks and other related approaches on a 2D circular wave prediction task. We show that DISTANA, when combined with a retrospective latent state inference principle called active tuning, can reliably derive hidden local causal factors. In a current weather prediction benchmark, DISTANA infers our planet's land-sea mask solely by observing temperature dynamics and uses the self inferred information to improve its own prediction of temperature. We are convinced that the retrospective inference of latent states in generative RNN architectures will play an essential role in future research on causal inference and explainable systems.

Inferring, Predicting, and Denoising Causal Wave Dynamics

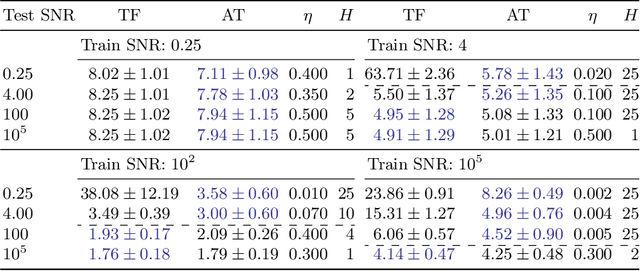
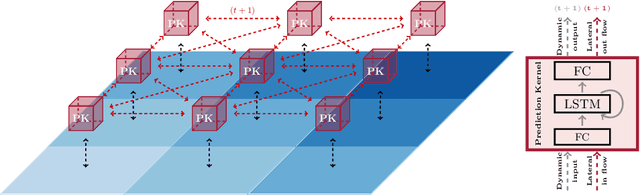
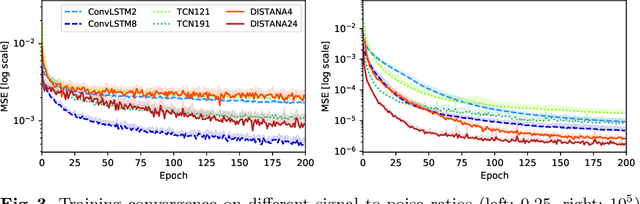
The novel DISTributed Artificial neural Network Architecture (DISTANA) is a generative, recurrent graph convolution neural network. It implements a grid or mesh of locally parameterizable laterally connected network modules. DISTANA is specifically designed to identify the causality behind spatially distributed, non-linear dynamical processes. We show that DISTANA is very well-suited to denoise data streams, given that re-occurring patterns are observed, significantly outperforming alternative approaches, such as temporal convolution networks and ConvLSTMs, on a complex spatial wave propagation benchmark. It produces stable and accurate closed-loop predictions even over hundreds of time steps. Moreover, it is able to effectively filter noise -- an ability that can be improved further by applying denoising autoencoder principles or by actively tuning latent neural state activities retrospectively. Results confirm that DISTANA is ready to model real-world spatio-temporal dynamics such as brain imaging, supply networks, water flow, or soil and weather data patterns.

A Distributed Neural Network Architecture for Robust Non-Linear Spatio-Temporal Prediction

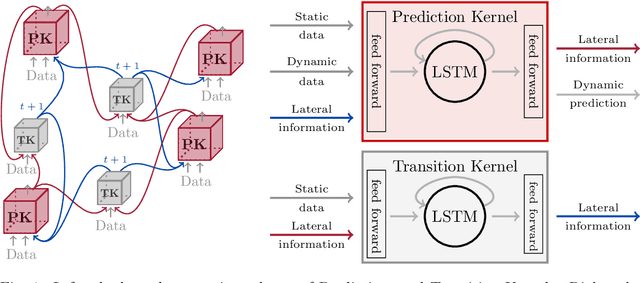
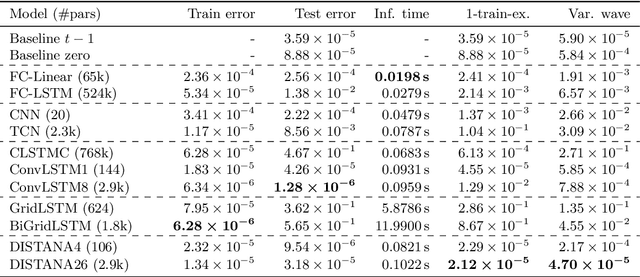
We introduce a distributed spatio-temporal artificial neural network architecture (DISTANA). It encodes mesh nodes using recurrent, neural prediction kernels (PKs), while neural transition kernels (TKs) transfer information between neighboring PKs, together modeling and predicting spatio-temporal time series dynamics. As a consequence, DISTANA assumes that generally applicable causes, which may be locally modified, generate the observed data. DISTANA learns in a parallel, spatially distributed manner, scales to large problem spaces, is capable of approximating complex dynamics, and is particularly robust to overfitting when compared to other competitive ANN models. Moreover, it is applicable to heterogeneously structured meshes.