The Deep Arbitrary Polynomial Chaos Neural Network or how Deep Artificial Neural Networks could benefit from Data-Driven Homogeneous Chaos Theory

Artificial Intelligence and Machine learning have been widely used in various fields of mathematical computing, physical modeling, computational science, communication science, and stochastic analysis. Approaches based on Deep Artificial Neural Networks (DANN) are very popular in our days. Depending on the learning task, the exact form of DANNs is determined via their multi-layer architecture, activation functions and the so-called loss function. However, for a majority of deep learning approaches based on DANNs, the kernel structure of neural signal processing remains the same, where the node response is encoded as a linear superposition of neural activity, while the non-linearity is triggered by the activation functions. In the current paper, we suggest to analyze the neural signal processing in DANNs from the point of view of homogeneous chaos theory as known from polynomial chaos expansion (PCE). From the PCE perspective, the (linear) response on each node of a DANN could be seen as a $1^{st}$ degree multi-variate polynomial of single neurons from the previous layer, i.e. linear weighted sum of monomials. From this point of view, the conventional DANN structure relies implicitly (but erroneously) on a Gaussian distribution of neural signals. Additionally, this view revels that by design DANNs do not necessarily fulfill any orthogonality or orthonormality condition for a majority of data-driven applications. Therefore, the prevailing handling of neural signals in DANNs could lead to redundant representation as any neural signal could contain some partial information from other neural signals. To tackle that challenge, we suggest to employ the data-driven generalization of PCE theory known as arbitrary polynomial chaos (aPC) to construct a corresponding multi-variate orthonormal representations on each node of a DANN to obtain Deep arbitrary polynomial chaos neural networks.

The sparse Polynomial Chaos expansion: a fully Bayesian approach with joint priors on the coefficients and global selection of terms

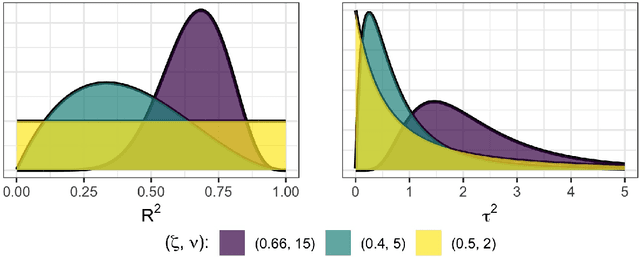
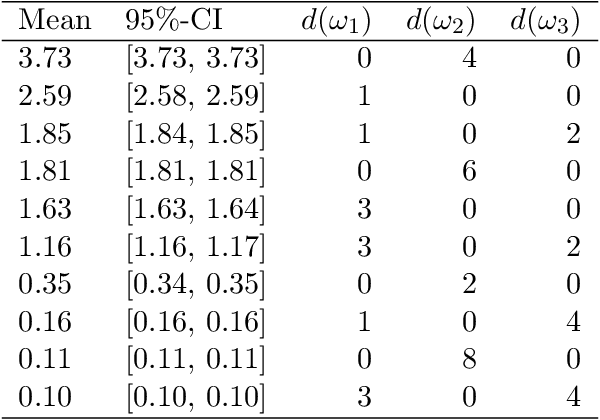
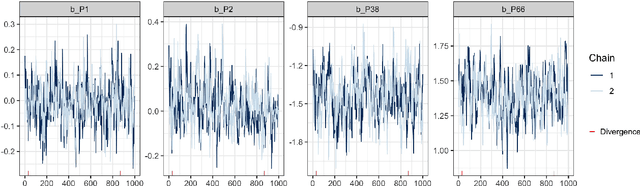
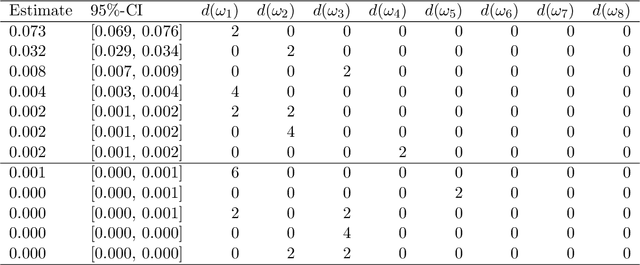
Polynomial chaos expansion (PCE) is a versatile tool widely used in uncertainty quantification and machine learning, but its successful application depends strongly on the accuracy and reliability of the resulting PCE-based response surface. High accuracy typically requires high polynomial degrees, demanding many training points especially in high-dimensional problems through the curse of dimensionality. So-called sparse PCE concepts work with a much smaller selection of basis polynomials compared to conventional PCE approaches and can overcome the curse of dimensionality very efficiently, but have to pay specific attention to their strategies of choosing training points. Furthermore, the approximation error resembles an uncertainty that most existing PCE-based methods do not estimate. In this study, we develop and evaluate a fully Bayesian approach to establish the PCE representation via joint shrinkage priors and Markov chain Monte Carlo. The suggested Bayesian PCE model directly aims to solve the two challenges named above: achieving a sparse PCE representation and estimating uncertainty of the PCE itself. The embedded Bayesian regularizing via the joint shrinkage prior allows using higher polynomial degrees for given training points due to its ability to handle underdetermined situations, where the number of considered PCE coefficients could be much larger than the number of available training points. We also explore multiple variable selection methods to construct sparse PCE expansions based on the established Bayesian representations, while globally selecting the most meaningful orthonormal polynomials given the available training data. We demonstrate the advantages of our Bayesian PCE and the corresponding sparsity-inducing methods on several benchmarks.