Optimal Embedding Guided Negative Sample Generation for Knowledge Graph Link Prediction

Knowledge graph embedding (KGE) models encode the structural information of knowledge graphs to predicting new links. Effective training of these models requires distinguishing between positive and negative samples with high precision. Although prior research has shown that improving the quality of negative samples can significantly enhance model accuracy, identifying high-quality negative samples remains a challenging problem. This paper theoretically investigates the condition under which negative samples lead to optimal KG embedding and identifies a sufficient condition for an effective negative sample distribution. Based on this theoretical foundation, we propose \textbf{E}mbedding \textbf{MU}tation (\textsc{EMU}), a novel framework that \emph{generates} negative samples satisfying this condition, in contrast to conventional methods that focus on \emph{identifying} challenging negative samples within the training data. Importantly, the simplicity of \textsc{EMU} ensures seamless integration with existing KGE models and negative sampling methods. To evaluate its efficacy, we conducted comprehensive experiments across multiple datasets. The results consistently demonstrate significant improvements in link prediction performance across various KGE models and negative sampling methods. Notably, \textsc{EMU} enables performance improvements comparable to those achieved by models with embedding dimension five times larger. An implementation of the method and experiments are available at https://github.com/nec-research/EMU-KG.

Fast, Modular, and Differentiable Framework for Machine Learning-Enhanced Molecular Simulations

We present an end-to-end differentiable molecular simulation framework (DIMOS) for molecular dynamics and Monte Carlo simulations. DIMOS easily integrates machine-learning-based interatomic potentials and implements classical force fields including particle-mesh Ewald electrostatics. Thanks to its modularity, both classical and machine-learning-based approaches can be easily combined into a hybrid description of the system (ML/MM). By supporting key molecular dynamics features such as efficient neighborlists and constraint algorithms for larger time steps, the framework bridges the gap between hand-optimized simulation engines and the flexibility of a PyTorch implementation. The superior performance and the high versatility is probed in different benchmarks and applications, with speed-up factors of up to $170\times$. The advantage of differentiability is demonstrated by an end-to-end optimization of the proposal distribution in a Markov Chain Monte Carlo simulation based on Hamiltonian Monte Carlo. Using these optimized simulation parameters a $3\times$ acceleration is observed in comparison to ad-hoc chosen simulation parameters. The code is available at https://github.com/nec-research/DIMOS.

Active Learning for Neural PDE Solvers

Solving partial differential equations (PDEs) is a fundamental problem in engineering and science. While neural PDE solvers can be more efficient than established numerical solvers, they often require large amounts of training data that is costly to obtain. Active Learning (AL) could help surrogate models reach the same accuracy with smaller training sets by querying classical solvers with more informative initial conditions and PDE parameters. While AL is more common in other domains, it has yet to be studied extensively for neural PDE solvers. To bridge this gap, we introduce AL4PDE, a modular and extensible active learning benchmark. It provides multiple parametric PDEs and state-of-the-art surrogate models for the solver-in-the-loop setting, enabling the evaluation of existing and the development of new AL methods for PDE solving. We use the benchmark to evaluate batch active learning algorithms such as uncertainty- and feature-based methods. We show that AL reduces the average error by up to 71% compared to random sampling and significantly reduces worst-case errors. Moreover, AL generates similar datasets across repeated runs, with consistent distributions over the PDE parameters and initial conditions. The acquired datasets are reusable, providing benefits for surrogate models not involved in the data generation.

Higher-Rank Irreducible Cartesian Tensors for Equivariant Message Passing

The ability to perform fast and accurate atomistic simulations is crucial for advancing the chemical sciences. By learning from high-quality data, machine-learned interatomic potentials achieve accuracy on par with ab initio and first-principles methods at a fraction of their computational cost. The success of machine-learned interatomic potentials arises from integrating inductive biases such as equivariance to group actions on an atomic system, e.g., equivariance to rotations and reflections. In particular, the field has notably advanced with the emergence of equivariant message-passing architectures. Most of these models represent an atomic system using spherical tensors, tensor products of which require complicated numerical coefficients and can be computationally demanding. This work introduces higher-rank irreducible Cartesian tensors as an alternative to spherical tensors, addressing the above limitations. We integrate irreducible Cartesian tensor products into message-passing neural networks and prove the equivariance of the resulting layers. Through empirical evaluations on various benchmark data sets, we consistently observe on-par or better performance than that of state-of-the-art spherical models.

Uncertainty-biased molecular dynamics for learning uniformly accurate interatomic potentials

Efficiently creating a concise but comprehensive data set for training machine-learned interatomic potentials (MLIPs) is an under-explored problem. Active learning (AL), which uses either biased or unbiased molecular dynamics (MD) simulations to generate candidate pools, aims to address this objective. Existing biased and unbiased MD simulations, however, are prone to miss either rare events or extrapolative regions -- areas of the configurational space where unreliable predictions are made. Simultaneously exploring both regions is necessary for developing uniformly accurate MLIPs. In this work, we demonstrate that MD simulations, when biased by the MLIP's energy uncertainty, effectively capture extrapolative regions and rare events without the need to know \textit{a priori} the system's transition temperatures and pressures. Exploiting automatic differentiation, we enhance bias-forces-driven MD simulations by introducing the concept of bias stress. We also employ calibrated ensemble-free uncertainties derived from sketched gradient features to yield MLIPs with similar or better accuracy than ensemble-based uncertainty methods at a lower computational cost. We use the proposed uncertainty-driven AL approach to develop MLIPs for two benchmark systems: alanine dipeptide and MIL-53(Al). Compared to MLIPs trained with conventional MD simulations, MLIPs trained with the proposed data-generation method more accurately represent the relevant configurational space for both atomic systems.

Learning Neural PDE Solvers with Parameter-Guided Channel Attention

Scientific Machine Learning (SciML) is concerned with the development of learned emulators of physical systems governed by partial differential equations (PDE). In application domains such as weather forecasting, molecular dynamics, and inverse design, ML-based surrogate models are increasingly used to augment or replace inefficient and often non-differentiable numerical simulation algorithms. While a number of ML-based methods for approximating the solutions of PDEs have been proposed in recent years, they typically do not adapt to the parameters of the PDEs, making it difficult to generalize to PDE parameters not seen during training. We propose a Channel Attention mechanism guided by PDE Parameter Embeddings (CAPE) component for neural surrogate models and a simple yet effective curriculum learning strategy. The CAPE module can be combined with neural PDE solvers allowing them to adapt to unseen PDE parameters. The curriculum learning strategy provides a seamless transition between teacher-forcing and fully auto-regressive training. We compare CAPE in conjunction with the curriculum learning strategy using a popular PDE benchmark and obtain consistent and significant improvements over the baseline models. The experiments also show several advantages of CAPE, such as its increased ability to generalize to unseen PDE parameters without large increases inference time and parameter count.

PDEBENCH: An Extensive Benchmark for Scientific Machine Learning

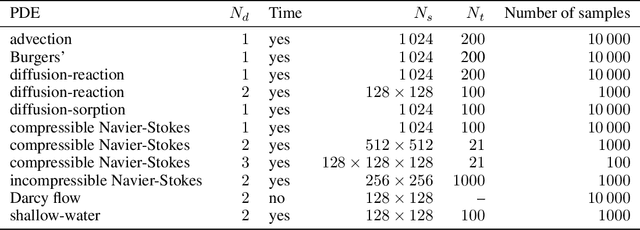
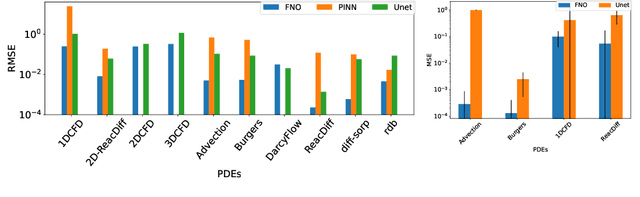
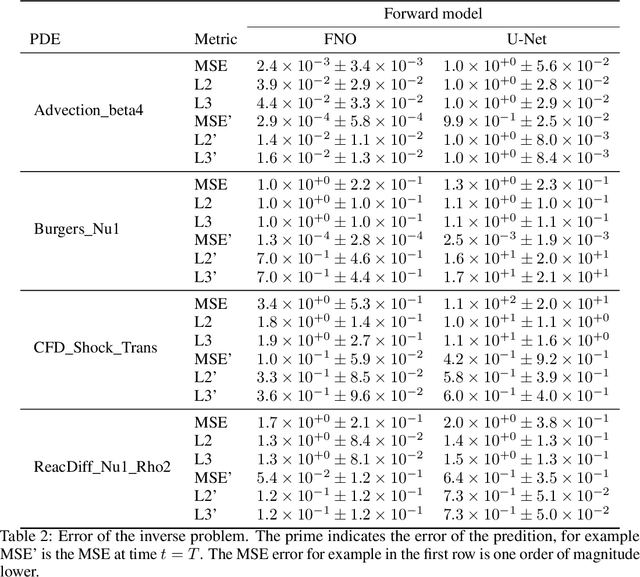
Machine learning-based modeling of physical systems has experienced increased interest in recent years. Despite some impressive progress, there is still a lack of benchmarks for Scientific ML that are easy to use but still challenging and representative of a wide range of problems. We introduce PDEBench, a benchmark suite of time-dependent simulation tasks based on Partial Differential Equations (PDEs). PDEBench comprises both code and data to benchmark the performance of novel machine learning models against both classical numerical simulations and machine learning baselines. Our proposed set of benchmark problems contribute the following unique features: (1) A much wider range of PDEs compared to existing benchmarks, ranging from relatively common examples to more realistic and difficult problems; (2) much larger ready-to-use datasets compared to prior work, comprising multiple simulation runs across a larger number of initial and boundary conditions and PDE parameters; (3) more extensible source codes with user-friendly APIs for data generation and baseline results with popular machine learning models (FNO, U-Net, PINN, Gradient-Based Inverse Method). PDEBench allows researchers to extend the benchmark freely for their own purposes using a standardized API and to compare the performance of new models to existing baseline methods. We also propose new evaluation metrics with the aim to provide a more holistic understanding of learning methods in the context of Scientific ML. With those metrics we identify tasks which are challenging for recent ML methods and propose these tasks as future challenges for the community. The code is available at https://github.com/pdebench/PDEBench.

Integrating diverse extraction pathways using iterative predictions for Multilingual Open Information Extraction

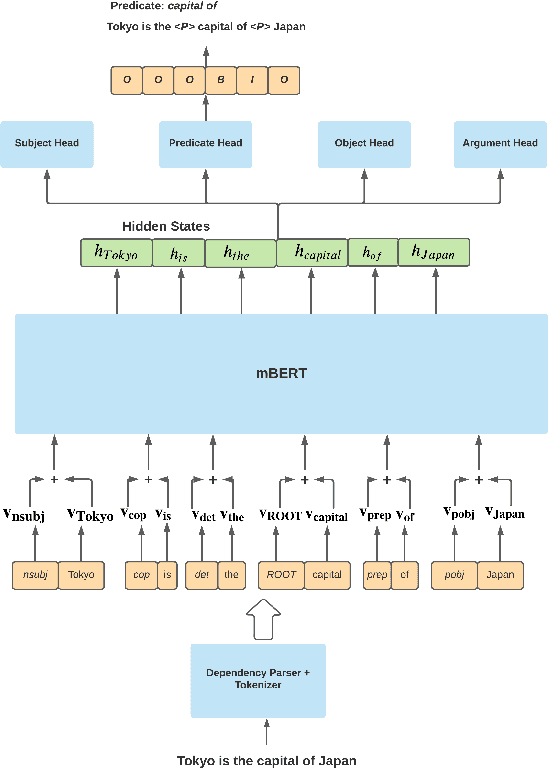
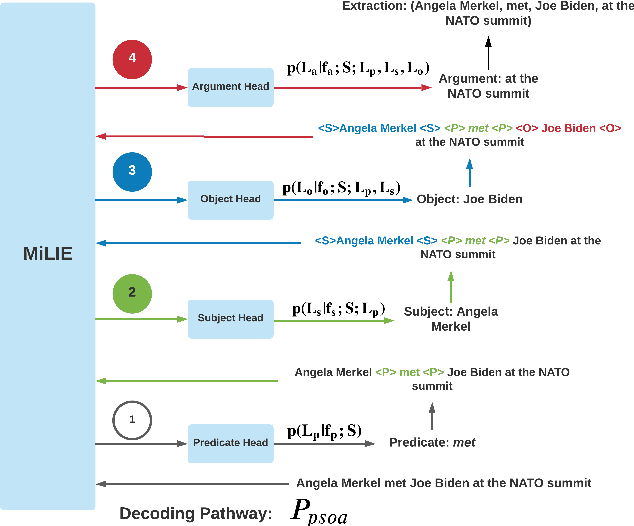
In this paper we investigate a simple hypothesis for the Open Information Extraction (OpenIE) task, that it may be easier to extract some elements of an triple if the extraction is conditioned on prior extractions which may be easier to extract. We successfully exploit this and propose a neural multilingual OpenIE system that iteratively extracts triples by conditioning extractions on different elements of the triple leading to a rich set of extractions. The iterative nature of MiLIE also allows for seamlessly integrating rule based extraction systems with a neural end-to-end system leading to improved performance. MiLIE outperforms SOTA systems on multiple languages ranging from Chinese to Galician thanks to it's ability of combining multiple extraction pathways. Our analysis confirms that it is indeed true that certain elements of an extraction are easier to extract than others. Finally, we introduce OpenIE evaluation datasets for two low resource languages namely Japanese and Galician.

An Empirical Study of the Effects of Sample-Mixing Methods for Efficient Training of Generative Adversarial Networks

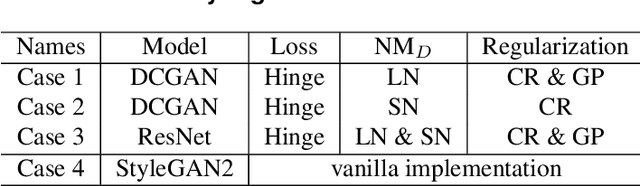
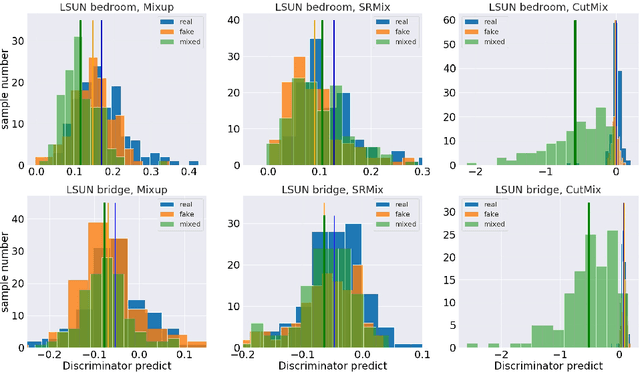
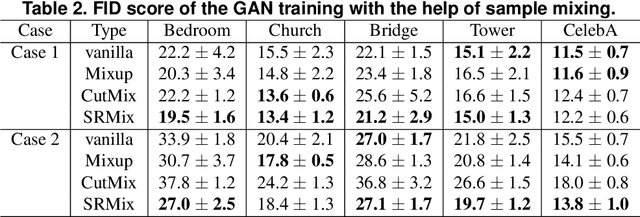
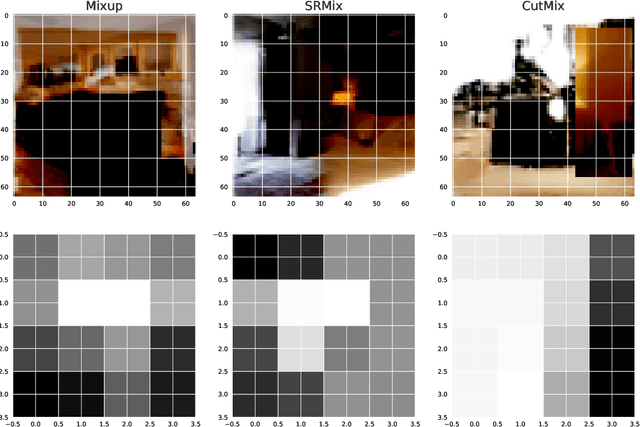
It is well-known that training of generative adversarial networks (GANs) requires huge iterations before the generator's providing good-quality samples. Although there are several studies to tackle this problem, there is still no universal solution. In this paper, we investigated the effect of sample mixing methods, that is, Mixup, CutMix, and newly proposed Smoothed Regional Mix (SRMix), to alleviate this problem. The sample-mixing methods are known to enhance the accuracy and robustness in the wide range of classification problems, and can naturally be applicable to GANs because the role of the discriminator can be interpreted as the classification between real and fake samples. We also proposed a new formalism applying the sample-mixing methods to GANs with the saturated losses which do not have a clear "label" of real and fake. We performed a vast amount of numerical experiments using LSUN and CelebA datasets. The results showed that Mixup and SRMix improved the quality of the generated images in terms of FID in most cases, in particular, SRMix showed the best improvement in most cases. Our analysis indicates that the mixed-samples can provide different properties from the vanilla fake samples, and the mixing pattern strongly affects the decision of the discriminators. The generated images of Mixup have good high-level feature but low-level feature is not so impressible. On the other hand, CutMix showed the opposite tendency. Our SRMix showed the middle tendency, that is, showed good high and low level features. We believe that our finding provides a new perspective to accelerate the GANs convergence and improve the quality of generated samples.

An Efficient Method of Training Small Models for Regression Problems with Knowledge Distillation

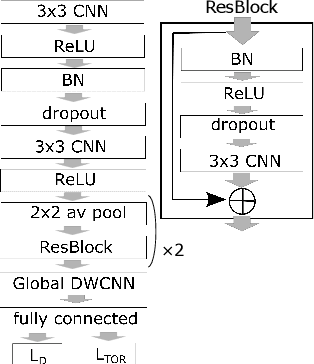
Compressing deep neural network (DNN) models becomes a very important and necessary technique for real-world applications, such as deploying those models on mobile devices. Knowledge distillation is one of the most popular methods for model compression, and many studies have been made on developing this technique. However, those studies mainly focused on classification problems, and very few attempts have been made on regression problems, although there are many application of DNNs on regression problems. In this paper, we propose a new formalism of knowledge distillation for regression problems. First, we propose a new loss function, teacher outlier rejection loss, which rejects outliers in training samples using teacher model predictions. Second, we consider a multi-task network with two outputs: one estimates training labels which is in general contaminated by noisy labels; And the other estimates teacher model's output which is expected to modify the noise labels following the memorization effects. By considering the multi-task network, training of the feature extraction of student models becomes more effective, and it allows us to obtain a better student model than one trained from scratch. We performed comprehensive evaluation with one simple toy model: sinusoidal function, and two open datasets: MPIIGaze, and Multi-PIE. Our results show consistent improvement in accuracy regardless of the annotation error level in the datasets.