Fast, Modular, and Differentiable Framework for Machine Learning-Enhanced Molecular Simulations

We present an end-to-end differentiable molecular simulation framework (DIMOS) for molecular dynamics and Monte Carlo simulations. DIMOS easily integrates machine-learning-based interatomic potentials and implements classical force fields including particle-mesh Ewald electrostatics. Thanks to its modularity, both classical and machine-learning-based approaches can be easily combined into a hybrid description of the system (ML/MM). By supporting key molecular dynamics features such as efficient neighborlists and constraint algorithms for larger time steps, the framework bridges the gap between hand-optimized simulation engines and the flexibility of a PyTorch implementation. The superior performance and the high versatility is probed in different benchmarks and applications, with speed-up factors of up to $170\times$. The advantage of differentiability is demonstrated by an end-to-end optimization of the proposal distribution in a Markov Chain Monte Carlo simulation based on Hamiltonian Monte Carlo. Using these optimized simulation parameters a $3\times$ acceleration is observed in comparison to ad-hoc chosen simulation parameters. The code is available at https://github.com/nec-research/DIMOS.

Geometric Kolmogorov-Arnold Superposition Theorem

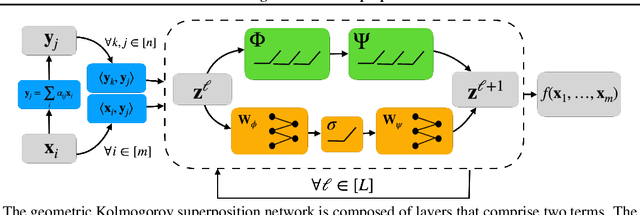
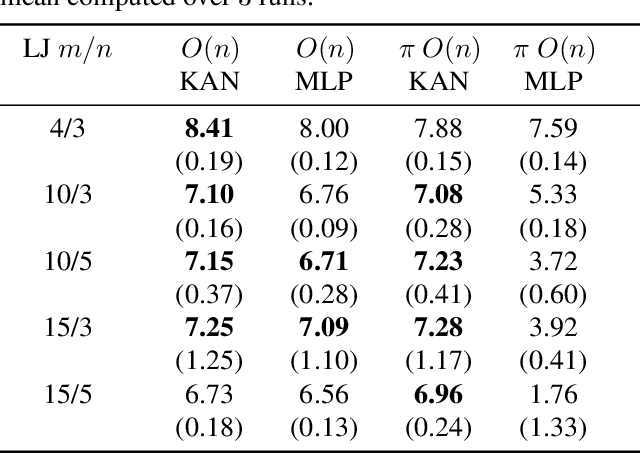
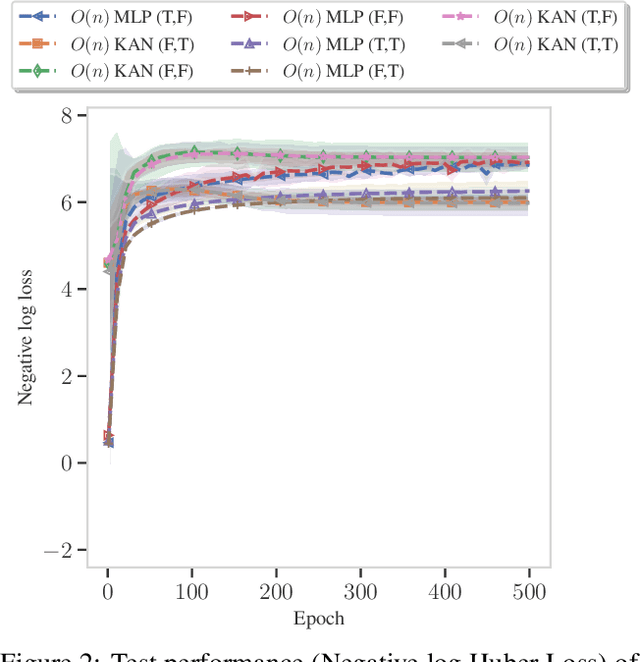
The Kolmogorov-Arnold Theorem (KAT), or more generally, the Kolmogorov Superposition Theorem (KST), establishes that any non-linear multivariate function can be exactly represented as a finite superposition of non-linear univariate functions. Unlike the universal approximation theorem, which provides only an approximate representation without guaranteeing a fixed network size, KST offers a theoretically exact decomposition. The Kolmogorov-Arnold Network (KAN) was introduced as a trainable model to implement KAT, and recent advancements have adapted KAN using concepts from modern neural networks. However, KAN struggles to effectively model physical systems that require inherent equivariance or invariance to $E(3)$ transformations, a key property for many scientific and engineering applications. In this work, we propose a novel extension of KAT and KAN to incorporate equivariance and invariance over $O(n)$ group actions, enabling accurate and efficient modeling of these systems. Our approach provides a unified approach that bridges the gap between mathematical theory and practical architectures for physical systems, expanding the applicability of KAN to a broader class of problems.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

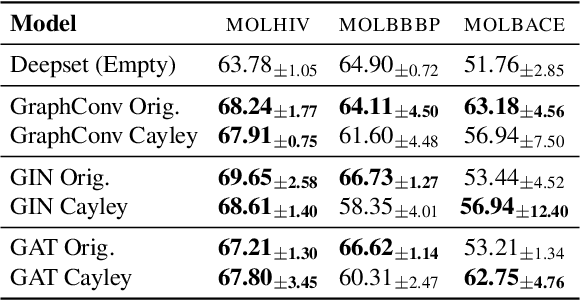
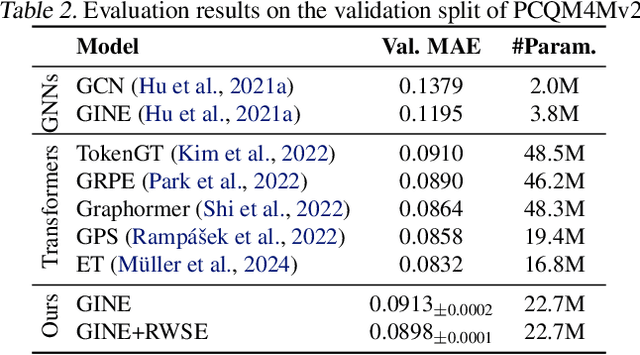
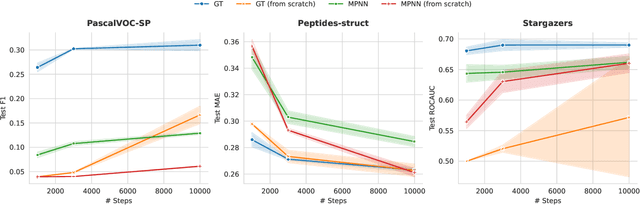
While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

Adaptive Width Neural Networks

For almost 70 years, researchers have mostly relied on hyper-parameter tuning to pick the width of neural networks' layers out of many possible choices. This paper challenges the status quo by introducing an easy-to-use technique to learn an unbounded width of a neural network's layer during training. The technique does not rely on alternate optimization nor hand-crafted gradient heuristics; rather, it jointly optimizes the width and the parameters of each layer via simple backpropagation. We apply the technique to a broad range of data domains such as tables, images, texts, and graphs, showing how the width adapts to the task's difficulty. By imposing a soft ordering of importance among neurons, it is possible to truncate the trained network at virtually zero cost, achieving a smooth trade-off between performance and compute resources in a structured way. Alternatively, one can dynamically compress the network with no performance degradation. In light of recent foundation models trained on large datasets, believed to require billions of parameters and where hyper-parameter tuning is unfeasible due to huge training costs, our approach stands as a viable alternative for width learning.

Higher-Rank Irreducible Cartesian Tensors for Equivariant Message Passing

The ability to perform fast and accurate atomistic simulations is crucial for advancing the chemical sciences. By learning from high-quality data, machine-learned interatomic potentials achieve accuracy on par with ab initio and first-principles methods at a fraction of their computational cost. The success of machine-learned interatomic potentials arises from integrating inductive biases such as equivariance to group actions on an atomic system, e.g., equivariance to rotations and reflections. In particular, the field has notably advanced with the emergence of equivariant message-passing architectures. Most of these models represent an atomic system using spherical tensors, tensor products of which require complicated numerical coefficients and can be computationally demanding. This work introduces higher-rank irreducible Cartesian tensors as an alternative to spherical tensors, addressing the above limitations. We integrate irreducible Cartesian tensor products into message-passing neural networks and prove the equivariance of the resulting layers. Through empirical evaluations on various benchmark data sets, we consistently observe on-par or better performance than that of state-of-the-art spherical models.

Structure-Aware E(3)-Invariant Molecular Conformer Aggregation Networks

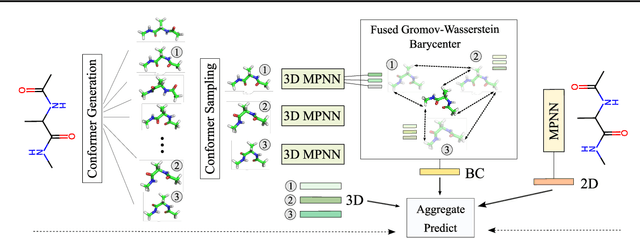
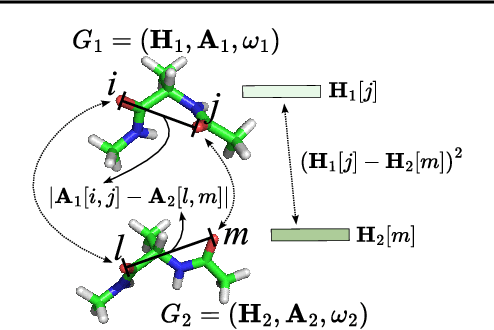
A molecule's 2D representation consists of its atoms, their attributes, and the molecule's covalent bonds. A 3D (geometric) representation of a molecule is called a conformer and consists of its atom types and Cartesian coordinates. Every conformer has a potential energy, and the lower this energy, the more likely it occurs in nature. Most existing machine learning methods for molecular property prediction consider either 2D molecular graphs or 3D conformer structure representations in isolation. Inspired by recent work on using ensembles of conformers in conjunction with 2D graph representations, we propose E(3)-invariant molecular conformer aggregation networks. The method integrates a molecule's 2D representation with that of multiple of its conformers. Contrary to prior work, we propose a novel 2D--3D aggregation mechanism based on a differentiable solver for the \emph{Fused Gromov-Wasserstein Barycenter} problem and the use of an efficient online conformer generation method based on distance geometry. We show that the proposed aggregation mechanism is E(3) invariant and provides an efficient GPU implementation. Moreover, we demonstrate that the aggregation mechanism helps to outperform state-of-the-art property prediction methods on established datasets significantly.

Adaptive Message Passing: A General Framework to Mitigate Oversmoothing, Oversquashing, and Underreaching

Long-range interactions are essential for the correct description of complex systems in many scientific fields. The price to pay for including them in the calculations, however, is a dramatic increase in the overall computational costs. Recently, deep graph networks have been employed as efficient, data-driven surrogate models for predicting properties of complex systems represented as graphs. These models rely on a local and iterative message passing strategy that should, in principle, capture long-range information without explicitly modeling the corresponding interactions. In practice, most deep graph networks cannot really model long-range dependencies due to the intrinsic limitations of (synchronous) message passing, namely oversmoothing, oversquashing, and underreaching. This work proposes a general framework that learns to mitigate these limitations: within a variational inference framework, we endow message passing architectures with the ability to freely adapt their depth and filter messages along the way. With theoretical and empirical arguments, we show that this simple strategy better captures long-range interactions, by surpassing the state of the art on five node and graph prediction datasets suited for this problem. Our approach consistently improves the performances of the baselines tested on these tasks. We complement the exposition with qualitative analyses and ablations to get a deeper understanding of the framework's inner workings.

Uncertainty-biased molecular dynamics for learning uniformly accurate interatomic potentials

Efficiently creating a concise but comprehensive data set for training machine-learned interatomic potentials (MLIPs) is an under-explored problem. Active learning (AL), which uses either biased or unbiased molecular dynamics (MD) simulations to generate candidate pools, aims to address this objective. Existing biased and unbiased MD simulations, however, are prone to miss either rare events or extrapolative regions -- areas of the configurational space where unreliable predictions are made. Simultaneously exploring both regions is necessary for developing uniformly accurate MLIPs. In this work, we demonstrate that MD simulations, when biased by the MLIP's energy uncertainty, effectively capture extrapolative regions and rare events without the need to know \textit{a priori} the system's transition temperatures and pressures. Exploiting automatic differentiation, we enhance bias-forces-driven MD simulations by introducing the concept of bias stress. We also employ calibrated ensemble-free uncertainties derived from sketched gradient features to yield MLIPs with similar or better accuracy than ensemble-based uncertainty methods at a lower computational cost. We use the proposed uncertainty-driven AL approach to develop MLIPs for two benchmark systems: alanine dipeptide and MIL-53(Al). Compared to MLIPs trained with conventional MD simulations, MLIPs trained with the proposed data-generation method more accurately represent the relevant configurational space for both atomic systems.

Thermally Averaged Magnetic Anisotropy Tensors via Machine Learning Based on Gaussian Moments

We propose a machine learning method to model molecular tensorial quantities, namely the magnetic anisotropy tensor, based on the Gaussian-moment neural-network approach. We demonstrate that the proposed methodology can achieve an accuracy of 0.3--0.4 cm$^{-1}$ and has excellent generalization capability for out-of-sample configurations. Moreover, in combination with machine-learned interatomic potential energies based on Gaussian moments, our approach can be applied to study the dynamic behavior of magnetic anisotropy tensors and provide a unique insight into spin-phonon relaxation.

Predicting Properties of Periodic Systems from Cluster Data: A Case Study of Liquid Water

The accuracy of the training data limits the accuracy of bulk properties from machine-learned potentials. For example, hybrid functionals or wave-function-based quantum chemical methods are readily available for cluster data but effectively out-of-scope for periodic structures. We show that local, atom-centred descriptors for machine-learned potentials enable the prediction of bulk properties from cluster model training data, agreeing reasonably well with predictions from bulk training data. We demonstrate such transferability by studying structural and dynamical properties of bulk liquid water with density functional theory and have found an excellent agreement with experimental as well as theoretical counterparts.