GraIP: A Benchmarking Framework For Neural Graph Inverse Problems

A wide range of graph learning tasks, such as structure discovery, temporal graph analysis, and combinatorial optimization, focus on inferring graph structures from data, rather than making predictions on given graphs. However, the respective methods to solve such problems are often developed in an isolated, task-specific manner and thus lack a unifying theoretical foundation. Here, we provide a stepping stone towards the formation of such a foundation and further development by introducing the Neural Graph Inverse Problem (GraIP) conceptual framework, which formalizes and reframes a broad class of graph learning tasks as inverse problems. Unlike discriminative approaches that directly predict target variables from given graph inputs, the GraIP paradigm addresses inverse problems, i.e., it relies on observational data and aims to recover the underlying graph structure by reversing the forward process, such as message passing or network dynamics, that produced the observed outputs. We demonstrate the versatility of GraIP across various graph learning tasks, including rewiring, causal discovery, and neural relational inference. We also propose benchmark datasets and metrics for each GraIP domain considered, and characterize and empirically evaluate existing baseline methods used to solve them. Overall, our unifying perspective bridges seemingly disparate applications and provides a principled approach to structural learning in constrained and combinatorial settings while encouraging cross-pollination of existing methods across graph inverse problems.

Principled Latent Diffusion for Graphs via Laplacian Autoencoders

Graph diffusion models achieve state-of-the-art performance in graph generation but suffer from quadratic complexity in the number of nodes -- and much of their capacity is wasted modeling the absence of edges in sparse graphs. Inspired by latent diffusion in other modalities, a natural idea is to compress graphs into a low-dimensional latent space and perform diffusion there. However, unlike images or text, graph generation requires nearly lossless reconstruction, as even a single error in decoding an adjacency matrix can render the entire sample invalid. This challenge has remained largely unaddressed. We propose LG-Flow, a latent graph diffusion framework that directly overcomes these obstacles. A permutation-equivariant autoencoder maps each node into a fixed-dimensional embedding from which the full adjacency is provably recoverable, enabling near-lossless reconstruction for both undirected graphs and DAGs. The dimensionality of this latent representation scales linearly with the number of nodes, eliminating the quadratic bottleneck and making it feasible to train larger and more expressive models. In this latent space, we train a Diffusion Transformer with flow matching, enabling efficient and expressive graph generation. Our approach achieves competitive results against state-of-the-art graph diffusion models, while achieving up to $1000\times$ speed-up.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

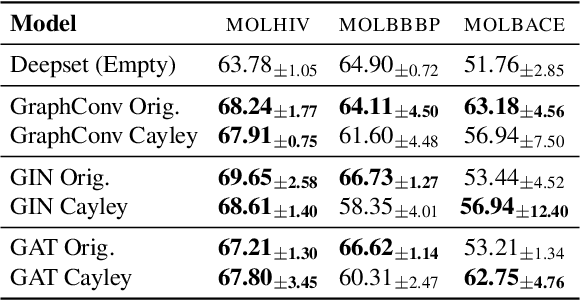
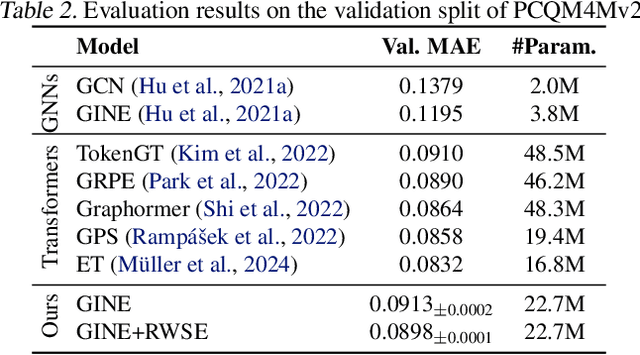
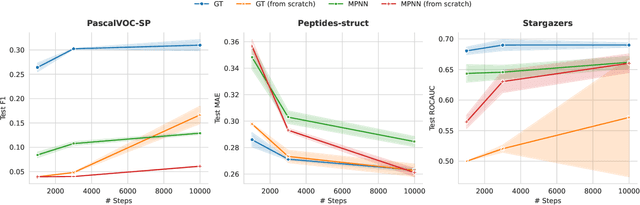
While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

Cometh: A continuous-time discrete-state graph diffusion model

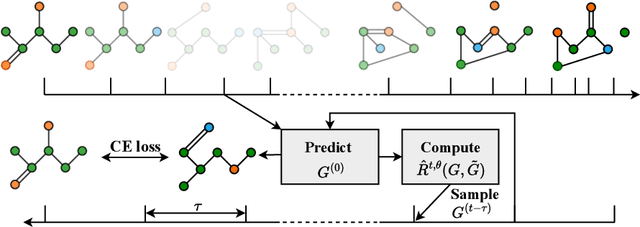
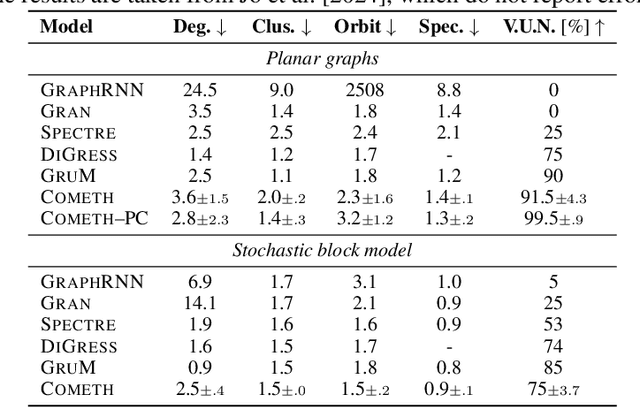
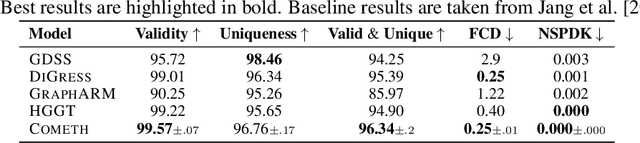
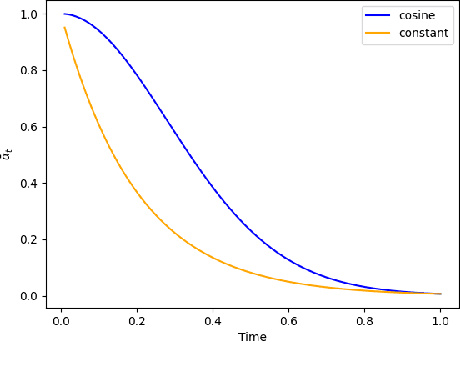
Discrete-state denoising diffusion models led to state-of-the-art performance in graph generation, especially in the molecular domain. Recently, they have been transposed to continuous time, allowing more flexibility in the reverse process and a better trade-off between sampling efficiency and quality. Here, to leverage the benefits of both approaches, we propose Cometh, a continuous-time discrete-state graph diffusion model, integrating graph data into a continuous-time diffusion model framework. Empirically, we show that integrating continuous time leads to significant improvements across various metrics over state-of-the-art discrete-state diffusion models on a large set of molecular and non-molecular benchmark datasets.

DiGress: Discrete Denoising diffusion for graph generation

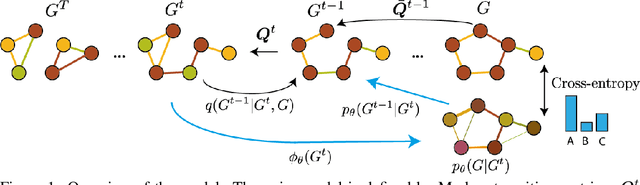
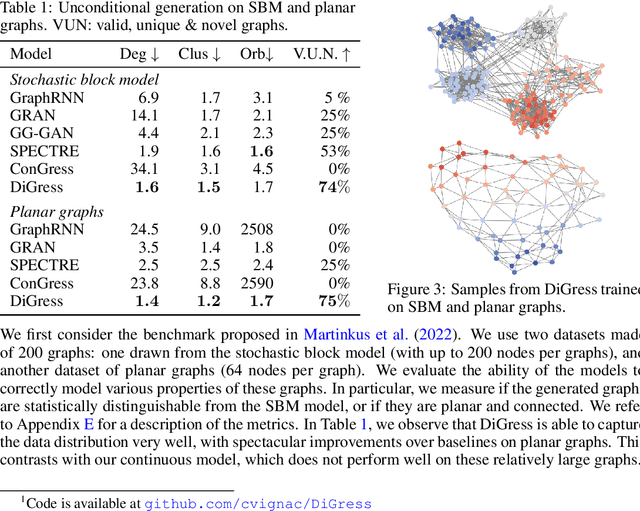
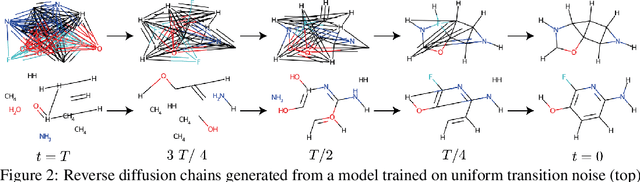
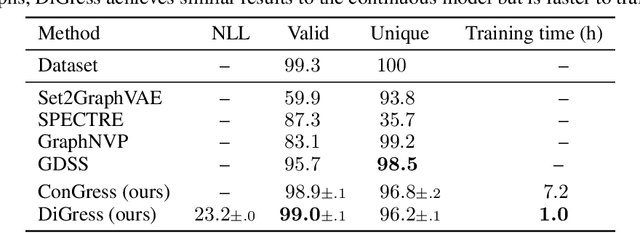
This work introduces DiGress, a discrete denoising diffusion model for generating graphs with categorical node and edge attributes. Our model defines a diffusion process that progressively edits a graph with noise (adding or removing edges, changing the categories), and a graph transformer network that learns to revert this process. With these two ingredients in place, we reduce distribution learning over graphs to a simple sequence of classification tasks. We further improve sample quality by proposing a new Markovian noise model that preserves the marginal distribution of node and edge types during diffusion, and by adding auxiliary graph-theoretic features derived from the noisy graph at each diffusion step. Finally, we propose a guidance procedure for conditioning the generation on graph-level features. Overall, DiGress achieves state-of-the-art performance on both molecular and non-molecular datasets, with up to 3x validity improvement on a dataset of planar graphs. In particular, it is the first model that scales to the large GuacaMol dataset containing 1.3M drug-like molecules without using a molecule-specific representation such as SMILES or fragments.