Distinguished In Uniform: Self Attention Vs. Virtual Nodes

Graph Transformers (GTs) such as SAN and GPS are graph processing models that combine Message-Passing GNNs (MPGNNs) with global Self-Attention. They were shown to be universal function approximators, with two reservations: 1. The initial node features must be augmented with certain positional encodings. 2. The approximation is non-uniform: Graphs of different sizes may require a different approximating network. We first clarify that this form of universality is not unique to GTs: Using the same positional encodings, also pure MPGNNs and even 2-layer MLPs are non-uniform universal approximators. We then consider uniform expressivity: The target function is to be approximated by a single network for graphs of all sizes. There, we compare GTs to the more efficient MPGNN + Virtual Node architecture. The essential difference between the two model definitions is in their global computation method -- Self-Attention Vs Virtual Node. We prove that none of the models is a uniform-universal approximator, before proving our main result: Neither model's uniform expressivity subsumes the other's. We demonstrate the theory with experiments on synthetic data. We further augment our study with real-world datasets, observing mixed results which indicate no clear ranking in practice as well.

Selecting Walk Schemes for Database Embedding

Machinery for data analysis often requires a numeric representation of the input. Towards that, a common practice is to embed components of structured data into a high-dimensional vector space. We study the embedding of the tuples of a relational database, where existing techniques are often based on optimization tasks over a collection of random walks from the database. The focus of this paper is on the recent FoRWaRD algorithm that is designed for dynamic databases, where walks are sampled by following foreign keys between tuples. Importantly, different walks have different schemas, or "walk schemes", that are derived by listing the relations and attributes along the walk. Also importantly, different walk schemes describe relationships of different natures in the database. We show that by focusing on a few informative walk schemes, we can obtain tuple embedding significantly faster, while retaining the quality. We define the problem of scheme selection for tuple embedding, devise several approaches and strategies for scheme selection, and conduct a thorough empirical study of the performance over a collection of downstream tasks. Our results confirm that with effective strategies for scheme selection, we can obtain high-quality embeddings considerably (e.g., three times) faster, preserve the extensibility to newly inserted tuples, and even achieve an increase in the precision of some tasks.

Where Did the Gap Go? Reassessing the Long-Range Graph Benchmark

The recent Long-Range Graph Benchmark (LRGB, Dwivedi et al. 2022) introduced a set of graph learning tasks strongly dependent on long-range interaction between vertices. Empirical evidence suggests that on these tasks Graph Transformers significantly outperform Message Passing GNNs (MPGNNs). In this paper, we carefully reevaluate multiple MPGNN baselines as well as the Graph Transformer GPS (Ramp\'a\v{s}ek et al. 2022) on LRGB. Through a rigorous empirical analysis, we demonstrate that the reported performance gap is overestimated due to suboptimal hyperparameter choices. It is noteworthy that across multiple datasets the performance gap completely vanishes after basic hyperparameter optimization. In addition, we discuss the impact of lacking feature normalization for LRGB's vision datasets and highlight a spurious implementation of LRGB's link prediction metric. The principal aim of our paper is to establish a higher standard of empirical rigor within the graph machine learning community.

WL meet VC

Recently, many works studied the expressive power of graph neural networks (GNNs) by linking it to the $1$-dimensional Weisfeiler--Leman algorithm ($1\text{-}\mathsf{WL}$). Here, the $1\text{-}\mathsf{WL}$ is a well-studied heuristic for the graph isomorphism problem, which iteratively colors or partitions a graph's vertex set. While this connection has led to significant advances in understanding and enhancing GNNs' expressive power, it does not provide insights into their generalization performance, i.e., their ability to make meaningful predictions beyond the training set. In this paper, we study GNNs' generalization ability through the lens of Vapnik--Chervonenkis (VC) dimension theory in two settings, focusing on graph-level predictions. First, when no upper bound on the graphs' order is known, we show that the bitlength of GNNs' weights tightly bounds their VC dimension. Further, we derive an upper bound for GNNs' VC dimension using the number of colors produced by the $1\text{-}\mathsf{WL}$. Secondly, when an upper bound on the graphs' order is known, we show a tight connection between the number of graphs distinguishable by the $1\text{-}\mathsf{WL}$ and GNNs' VC dimension. Our empirical study confirms the validity of our theoretical findings.

One Model, Any CSP: Graph Neural Networks as Fast Global Search Heuristics for Constraint Satisfaction

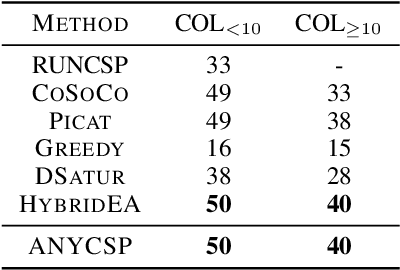
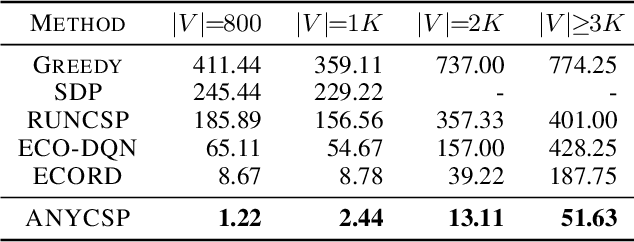
We propose a universal Graph Neural Network architecture which can be trained as an end-2-end search heuristic for any Constraint Satisfaction Problem (CSP). Our architecture can be trained unsupervised with policy gradient descent to generate problem specific heuristics for any CSP in a purely data driven manner. The approach is based on a novel graph representation for CSPs that is both generic and compact and enables us to process every possible CSP instance with one GNN, regardless of constraint arity, relations or domain size. Unlike previous RL-based methods, we operate on a global search action space and allow our GNN to modify any number of variables in every step of the stochastic search. This enables our method to properly leverage the inherent parallelism of GNNs. We perform a thorough empirical evaluation where we learn heuristics for well known and important CSPs from random data, including graph coloring, MaxCut, 3-SAT and MAX-k-SAT. Our approach outperforms prior approaches for neural combinatorial optimization by a substantial margin. It can compete with, and even improve upon, conventional search heuristics on test instances that are several orders of magnitude larger and structurally more complex than those seen during training.