One Model, Any CSP: Graph Neural Networks as Fast Global Search Heuristics for Constraint Satisfaction
Paper and Code
Aug 22, 2022
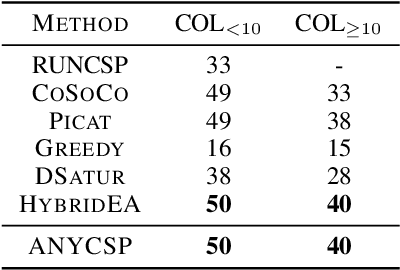

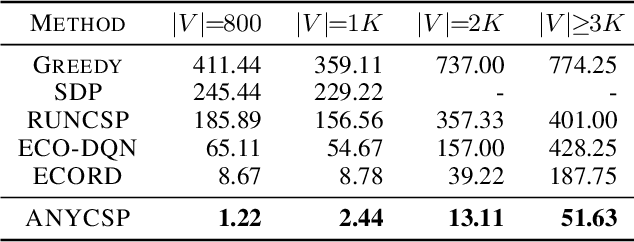
We propose a universal Graph Neural Network architecture which can be trained as an end-2-end search heuristic for any Constraint Satisfaction Problem (CSP). Our architecture can be trained unsupervised with policy gradient descent to generate problem specific heuristics for any CSP in a purely data driven manner. The approach is based on a novel graph representation for CSPs that is both generic and compact and enables us to process every possible CSP instance with one GNN, regardless of constraint arity, relations or domain size. Unlike previous RL-based methods, we operate on a global search action space and allow our GNN to modify any number of variables in every step of the stochastic search. This enables our method to properly leverage the inherent parallelism of GNNs. We perform a thorough empirical evaluation where we learn heuristics for well known and important CSPs from random data, including graph coloring, MaxCut, 3-SAT and MAX-k-SAT. Our approach outperforms prior approaches for neural combinatorial optimization by a substantial margin. It can compete with, and even improve upon, conventional search heuristics on test instances that are several orders of magnitude larger and structurally more complex than those seen during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge