Question: How do Large Language Models perform on the Question Answering tasks? Answer:

Large Language Models (LLMs) have been showing promising results for various NLP-tasks without the explicit need to be trained for these tasks by using few-shot or zero-shot prompting techniques. A common NLP-task is question-answering (QA). In this study, we propose a comprehensive performance comparison between smaller fine-tuned models and out-of-the-box instruction-following LLMs on the Stanford Question Answering Dataset 2.0 (SQuAD2), specifically when using a single-inference prompting technique. Since the dataset contains unanswerable questions, previous work used a double inference method. We propose a prompting style which aims to elicit the same ability without the need for double inference, saving compute time and resources. Furthermore, we investigate their generalization capabilities by comparing their performance on similar but different QA datasets, without fine-tuning neither model, emulating real-world uses where the context and questions asked may differ from the original training distribution, for example swapping Wikipedia for news articles. Our results show that smaller, fine-tuned models outperform current State-Of-The-Art (SOTA) LLMs on the fine-tuned task, but recent SOTA models are able to close this gap on the out-of-distribution test and even outperform the fine-tuned models on 3 of the 5 tested QA datasets.

One Model, Any CSP: Graph Neural Networks as Fast Global Search Heuristics for Constraint Satisfaction

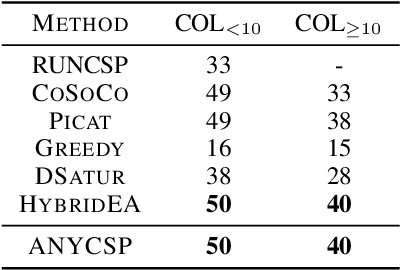
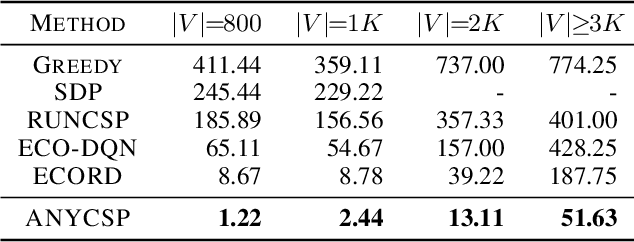
We propose a universal Graph Neural Network architecture which can be trained as an end-2-end search heuristic for any Constraint Satisfaction Problem (CSP). Our architecture can be trained unsupervised with policy gradient descent to generate problem specific heuristics for any CSP in a purely data driven manner. The approach is based on a novel graph representation for CSPs that is both generic and compact and enables us to process every possible CSP instance with one GNN, regardless of constraint arity, relations or domain size. Unlike previous RL-based methods, we operate on a global search action space and allow our GNN to modify any number of variables in every step of the stochastic search. This enables our method to properly leverage the inherent parallelism of GNNs. We perform a thorough empirical evaluation where we learn heuristics for well known and important CSPs from random data, including graph coloring, MaxCut, 3-SAT and MAX-k-SAT. Our approach outperforms prior approaches for neural combinatorial optimization by a substantial margin. It can compete with, and even improve upon, conventional search heuristics on test instances that are several orders of magnitude larger and structurally more complex than those seen during training.