Spectral Graph Neural Networks are Incomplete on Graphs with a Simple Spectrum

Spectral features are widely incorporated within Graph Neural Networks (GNNs) to improve their expressive power, or their ability to distinguish among non-isomorphic graphs. One popular example is the usage of graph Laplacian eigenvectors for positional encoding in MPNNs and Graph Transformers. The expressive power of such Spectrally-enhanced GNNs (SGNNs) is usually evaluated via the k-WL graph isomorphism test hierarchy and homomorphism counting. Yet, these frameworks align poorly with the graph spectra, yielding limited insight into SGNNs' expressive power. We leverage a well-studied paradigm of classifying graphs by their largest eigenvalue multiplicity to introduce an expressivity hierarchy for SGNNs. We then prove that many SGNNs are incomplete even on graphs with distinct eigenvalues. To mitigate this deficiency, we adapt rotation equivariant neural networks to the graph spectra setting to propose a method to provably improve SGNNs' expressivity on simple spectrum graphs. We empirically verify our theoretical claims via an image classification experiment on the MNIST Superpixel dataset and eigenvector canonicalization on graphs from ZINC.

Interpretable Graph Learning Over Sets of Temporally-Sparse Data

Real-world medical data often includes measurements from multiple signals that are collected at irregular and asynchronous time intervals. For example, different types of blood tests can be measured at different times and frequencies, resulting in fragmented and unevenly scattered temporal data. Similar issues of irregular sampling of different attributes occur in other domains, such as monitoring of large systems using event log files or the spread of fake news on social networks. Effectively learning from such data requires models that can handle sets of temporally sparse and heterogeneous signals. In this paper, we propose Graph Mixing Additive Networks (GMAN), a novel and interpretable-by-design model for learning over irregular sets of temporal signals. Our method achieves state-of-the-art performance in real-world medical tasks, including a 4-point increase in the AUROC score of in-hospital mortality prediction, compared to existing methods. We further showcase GMAN's flexibility by applying it to a fake news detection task. We demonstrate how its interpretability capabilities, including node-level, graph-level, and subset-level importance, allow for transition phases detection and gaining medical insights with real-world high-stakes implications. Finally, we provide theoretical insights on GMAN expressive power.

Identifying Critical Phases for Disease Onset with Sparse Haematological Biomarkers

Routinely collected clinical blood tests are an emerging molecular data source for large-scale biomedical research but inherently feature irregular sampling and informative observation. Traditional approaches rely on imputation, which can distort learning signals and bias predictions while lacking biological interpretability. We propose a novel methodology using Graph Neural Additive Networks (GNAN) to model biomarker trajectories as time-weighted directed graphs, where nodes represent sampling events and edges encode the time delta between events. GNAN's additive structure enables the explicit decomposition of feature and temporal contributions, allowing the detection of critical disease-associated time points. Unlike conventional imputation-based approaches, our method preserves the temporal structure of sparse data without introducing artificial biases and provides inherently interpretable predictions by decomposing contributions from each biomarker and time interval. This makes our model clinically applicable, as well as allowing it to discover biologically meaningful disease signatures.

Depth-Width tradeoffs in Algorithmic Reasoning of Graph Tasks with Transformers

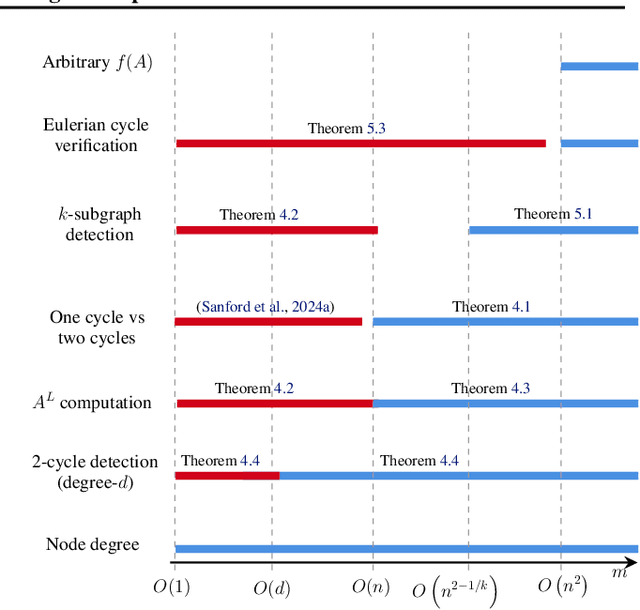
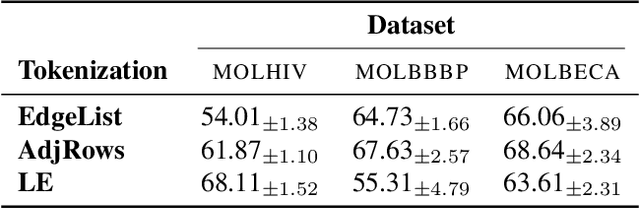
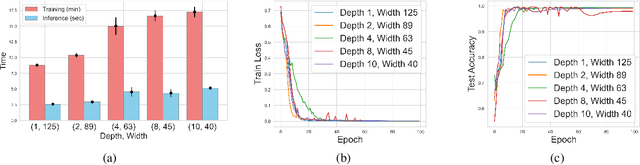
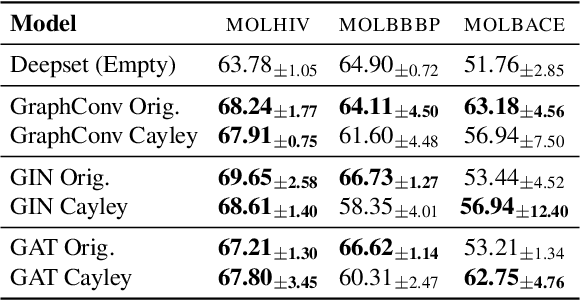
Transformers have revolutionized the field of machine learning. In particular, they can be used to solve complex algorithmic problems, including graph-based tasks. In such algorithmic tasks a key question is what is the minimal size of a transformer that can implement a task. Recent work has begun to explore this problem for graph-based tasks, showing that for sub-linear embedding dimension (i.e., model width) logarithmic depth suffices. However, an open question, which we address here, is what happens if width is allowed to grow linearly. Here we analyze this setting, and provide the surprising result that with linear width, constant depth suffices for solving a host of graph-based problems. This suggests that a moderate increase in width can allow much shallower models, which are advantageous in terms of inference time. For other problems, we show that quadratic width is required. Our results demonstrate the complex and intriguing landscape of transformer implementations of graph-based algorithms. We support our theoretical results with empirical evaluations.

Position: Graph Learning Will Lose Relevance Due To Poor Benchmarks

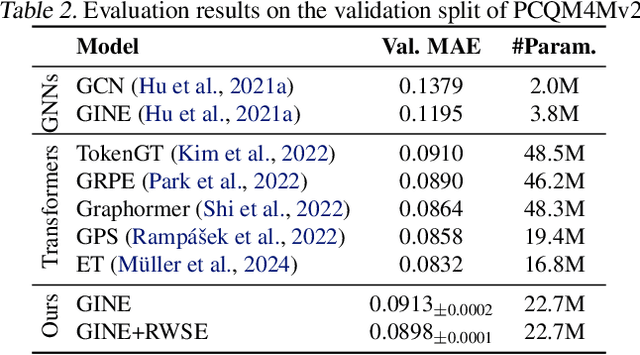
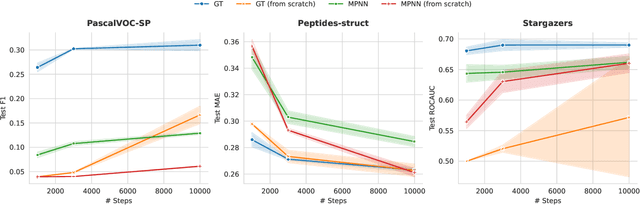
While machine learning on graphs has demonstrated promise in drug design and molecular property prediction, significant benchmarking challenges hinder its further progress and relevance. Current benchmarking practices often lack focus on transformative, real-world applications, favoring narrow domains like two-dimensional molecular graphs over broader, impactful areas such as combinatorial optimization, relational databases, or chip design. Additionally, many benchmark datasets poorly represent the underlying data, leading to inadequate abstractions and misaligned use cases. Fragmented evaluations and an excessive focus on accuracy further exacerbate these issues, incentivizing overfitting rather than fostering generalizable insights. These limitations have prevented the development of truly useful graph foundation models. This position paper calls for a paradigm shift toward more meaningful benchmarks, rigorous evaluation protocols, and stronger collaboration with domain experts to drive impactful and reliable advances in graph learning research, unlocking the potential of graph learning.

Towards Invariance to Node Identifiers in Graph Neural Networks

Message-Passing Graph Neural Networks (GNNs) are known to have limited expressive power, due to their message passing structure. One mechanism for circumventing this limitation is to add unique node identifiers (IDs), which break the symmetries that underlie the expressivity limitation. In this work, we highlight a key limitation of the ID framework, and propose an approach for addressing it. We begin by observing that the final output of the GNN should clearly not depend on the specific IDs used. We then show that in practice this does not hold, and thus the learned network does not possess this desired structural property. Such invariance to node IDs may be enforced in several ways, and we discuss their theoretical properties. We then propose a novel regularization method that effectively enforces ID invariance to the network. Extensive evaluations on both real-world and synthetic tasks demonstrate that our approach significantly improves ID invariance and, in turn, often boosts generalization performance.

On the Utilization of Unique Node Identifiers in Graph Neural Networks

Graph neural networks have inherent representational limitations due to their message-passing structure. Recent work has suggested that these limitations can be overcome by using unique node identifiers (UIDs). Here we argue that despite the advantages of UIDs, one of their disadvantages is that they lose the desirable property of permutation-equivariance. We thus propose to focus on UID models that are permutation-equivariant, and present theoretical arguments for their advantages. Motivated by this, we propose a method to regularize UID models towards permutation equivariance, via a contrastive loss. We empirically demonstrate that our approach improves generalization and extrapolation abilities while providing faster training convergence. On the recent BREC expressiveness benchmark, our proposed method achieves state-of-the-art performance compared to other random-based approaches.

A General Recipe for Contractive Graph Neural Networks -- Technical Report

Graph Neural Networks (GNNs) have gained significant popularity for learning representations of graph-structured data due to their expressive power and scalability. However, despite their success in domains such as social network analysis, recommendation systems, and bioinformatics, GNNs often face challenges related to stability, generalization, and robustness to noise and adversarial attacks. Regularization techniques have shown promise in addressing these challenges by controlling model complexity and improving robustness. Building on recent advancements in contractive GNN architectures, this paper presents a novel method for inducing contractive behavior in any GNN through SVD regularization. By deriving a sufficient condition for contractiveness in the update step and applying constraints on network parameters, we demonstrate the impact of SVD regularization on the Lipschitz constant of GNNs. Our findings highlight the role of SVD regularization in enhancing the stability and generalization of GNNs, contributing to the development of more robust graph-based learning algorithms dynamics.

Cayley Graph Propagation

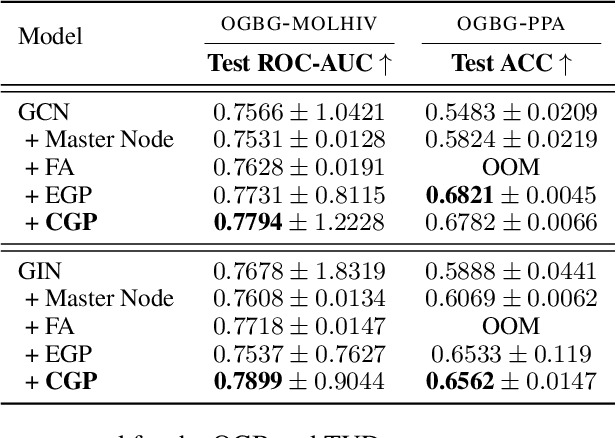
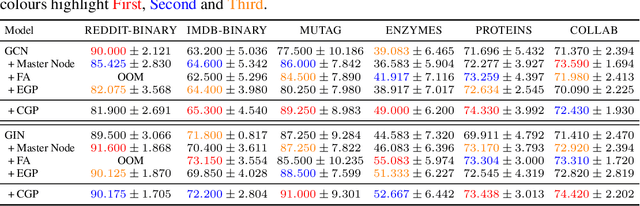
In spite of the plethora of success stories with graph neural networks (GNNs) on modelling graph-structured data, they are notoriously vulnerable to over-squashing, whereby tasks necessitate the mixing of information between distance pairs of nodes. To address this problem, prior work suggests rewiring the graph structure to improve information flow. Alternatively, a significant body of research has dedicated itself to discovering and precomputing bottleneck-free graph structures to ameliorate over-squashing. One well regarded family of bottleneck-free graphs within the mathematical community are expander graphs, with prior work$\unicode{x2014}$Expander Graph Propagation (EGP)$\unicode{x2014}$proposing the use of a well-known expander graph family$\unicode{x2014}$the Cayley graphs of the $\mathrm{SL}(2,\mathbb{Z}_n)$ special linear group$\unicode{x2014}$as a computational template for GNNs. However, in EGP the computational graphs used are truncated to align with a given input graph. In this work, we show that truncation is detrimental to the coveted expansion properties. Instead, we propose CGP, a method to propagate information over a complete Cayley graph structure, thereby ensuring it is bottleneck-free to better alleviate over-squashing. Our empirical evidence across several real-world datasets not only shows that CGP recovers significant improvements as compared to EGP, but it is also akin to or outperforms computationally complex graph rewiring techniques.

The Intelligible and Effective Graph Neural Additive Networks

Graph Neural Networks (GNNs) have emerged as the predominant approach for learning over graph-structured data. However, most GNNs operate as black-box models and require post-hoc explanations, which may not suffice in high-stakes scenarios where transparency is crucial. In this paper, we present a GNN that is interpretable by design. Our model, Graph Neural Additive Network (GNAN), is a novel extension of the interpretable class of Generalized Additive Models, and can be visualized and fully understood by humans. GNAN is designed to be fully interpretable, allowing both global and local explanations at the feature and graph levels through direct visualization of the model. These visualizations describe the exact way the model uses the relationships between the target variable, the features, and the graph. We demonstrate the intelligibility of GNANs in a series of examples on different tasks and datasets. In addition, we show that the accuracy of GNAN is on par with black-box GNNs, making it suitable for critical applications where transparency is essential, alongside high accuracy.