Depth-Width tradeoffs in Algorithmic Reasoning of Graph Tasks with Transformers

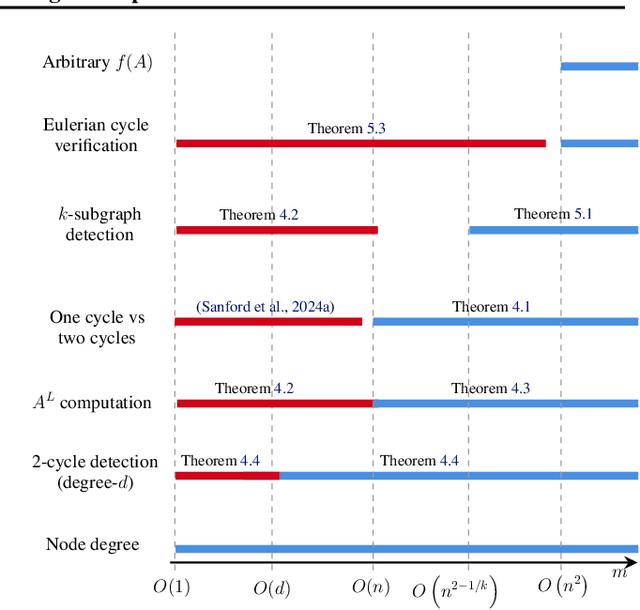
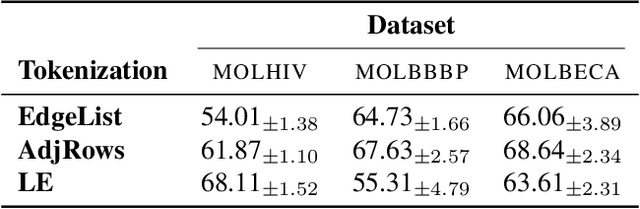
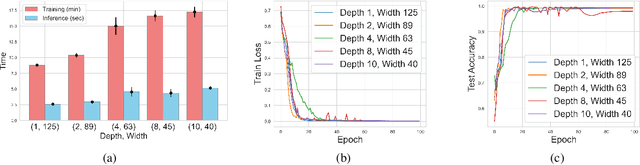
Transformers have revolutionized the field of machine learning. In particular, they can be used to solve complex algorithmic problems, including graph-based tasks. In such algorithmic tasks a key question is what is the minimal size of a transformer that can implement a task. Recent work has begun to explore this problem for graph-based tasks, showing that for sub-linear embedding dimension (i.e., model width) logarithmic depth suffices. However, an open question, which we address here, is what happens if width is allowed to grow linearly. Here we analyze this setting, and provide the surprising result that with linear width, constant depth suffices for solving a host of graph-based problems. This suggests that a moderate increase in width can allow much shallower models, which are advantageous in terms of inference time. For other problems, we show that quadratic width is required. Our results demonstrate the complex and intriguing landscape of transformer implementations of graph-based algorithms. We support our theoretical results with empirical evaluations.

Optimal Sample Complexity of Contrastive Learning

Contrastive learning is a highly successful technique for learning representations of data from labeled tuples, specifying the distance relations within the tuple. We study the sample complexity of contrastive learning, i.e. the minimum number of labeled tuples sufficient for getting high generalization accuracy. We give tight bounds on the sample complexity in a variety of settings, focusing on arbitrary distance functions, both general $\ell_p$-distances, and tree metrics. Our main result is an (almost) optimal bound on the sample complexity of learning $\ell_p$-distances for integer $p$. For any $p \ge 1$ we show that $\tilde \Theta(\min(nd,n^2))$ labeled tuples are necessary and sufficient for learning $d$-dimensional representations of $n$-point datasets. Our results hold for an arbitrary distribution of the input samples and are based on giving the corresponding bounds on the Vapnik-Chervonenkis/Natarajan dimension of the associated problems. We further show that the theoretical bounds on sample complexity obtained via VC/Natarajan dimension can have strong predictive power for experimental results, in contrast with the folklore belief about a substantial gap between the statistical learning theory and the practice of deep learning.

Tree Learning: Optimal Algorithms and Sample Complexity

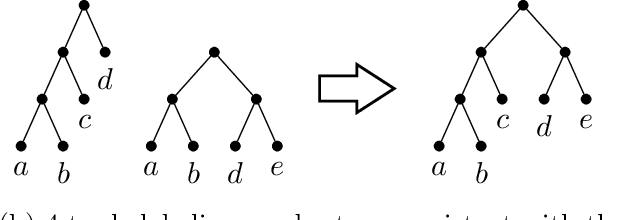
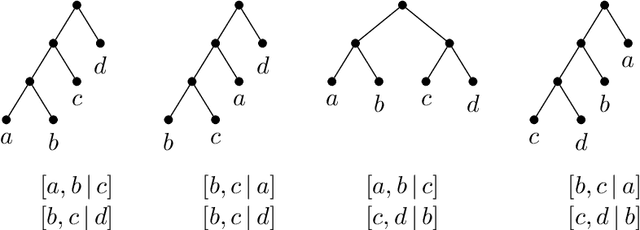
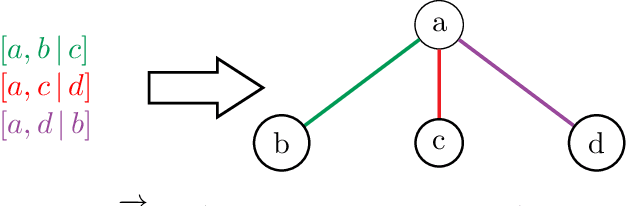
We study the problem of learning a hierarchical tree representation of data from labeled samples, taken from an arbitrary (and possibly adversarial) distribution. Consider a collection of data tuples labeled according to their hierarchical structure. The smallest number of such tuples required in order to be able to accurately label subsequent tuples is of interest for data collection in machine learning. We present optimal sample complexity bounds for this problem in several learning settings, including (agnostic) PAC learning and online learning. Our results are based on tight bounds of the Natarajan and Littlestone dimensions of the associated problem. The corresponding tree classifiers can be constructed efficiently in near-linear time.