Federated Learning Clients Clustering with Adaptation to Data Drifts

Federated Learning (FL) enables deep learning model training across edge devices and protects user privacy by retaining raw data locally. Data heterogeneity in client distributions slows model convergence and leads to plateauing with reduced precision. Clustered FL solutions address this by grouping clients with statistically similar data and training models for each cluster. However, maintaining consistent client similarity within each group becomes challenging when data drifts occur, significantly impacting model accuracy. In this paper, we introduce Fielding, a clustered FL framework that handles data drifts promptly with low overheads. Fielding detects drifts on all clients and performs selective label distribution-based re-clustering to balance cluster optimality and model performance, remaining robust to malicious clients and varied heterogeneity degrees. Our evaluations show that Fielding improves model final accuracy by 1.9%-5.9% and reaches target accuracies 1.16x-2.61x faster.

Noise is All You Need: Private Second-Order Convergence of Noisy SGD

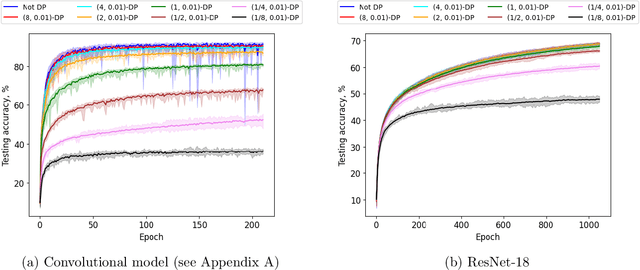
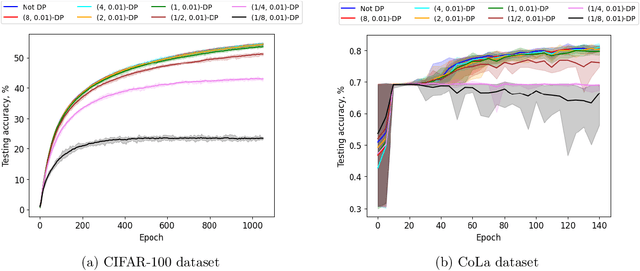
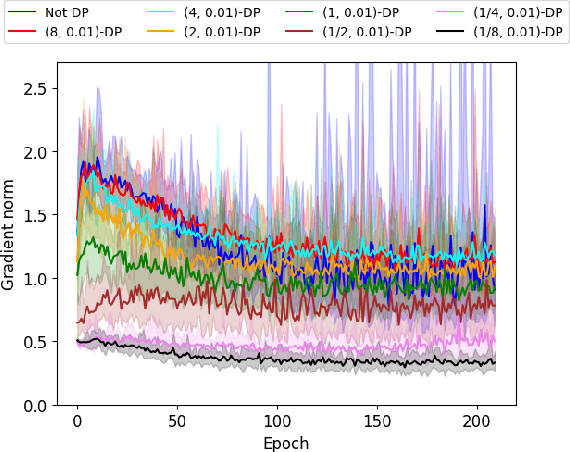
Private optimization is a topic of major interest in machine learning, with differentially private stochastic gradient descent (DP-SGD) playing a key role in both theory and practice. Furthermore, DP-SGD is known to be a powerful tool in contexts beyond privacy, including robustness, machine unlearning, etc. Existing analyses of DP-SGD either make relatively strong assumptions (e.g., Lipschitz continuity of the loss function, or even convexity) or prove only first-order convergence (and thus might end at a saddle point in the non-convex setting). At the same time, there has been progress in proving second-order convergence of the non-private version of ``noisy SGD'', as well as progress in designing algorithms that are more complex than DP-SGD and do guarantee second-order convergence. We revisit DP-SGD and show that ``noise is all you need'': the noise necessary for privacy already implies second-order convergence under the standard smoothness assumptions, even for non-Lipschitz loss functions. Hence, we get second-order convergence essentially for free: DP-SGD, the workhorse of modern private optimization, under minimal assumptions can be used to find a second-order stationary point.

Optimal Sample Complexity of Contrastive Learning

Contrastive learning is a highly successful technique for learning representations of data from labeled tuples, specifying the distance relations within the tuple. We study the sample complexity of contrastive learning, i.e. the minimum number of labeled tuples sufficient for getting high generalization accuracy. We give tight bounds on the sample complexity in a variety of settings, focusing on arbitrary distance functions, both general $\ell_p$-distances, and tree metrics. Our main result is an (almost) optimal bound on the sample complexity of learning $\ell_p$-distances for integer $p$. For any $p \ge 1$ we show that $\tilde \Theta(\min(nd,n^2))$ labeled tuples are necessary and sufficient for learning $d$-dimensional representations of $n$-point datasets. Our results hold for an arbitrary distribution of the input samples and are based on giving the corresponding bounds on the Vapnik-Chervonenkis/Natarajan dimension of the associated problems. We further show that the theoretical bounds on sample complexity obtained via VC/Natarajan dimension can have strong predictive power for experimental results, in contrast with the folklore belief about a substantial gap between the statistical learning theory and the practice of deep learning.

Tree Learning: Optimal Algorithms and Sample Complexity

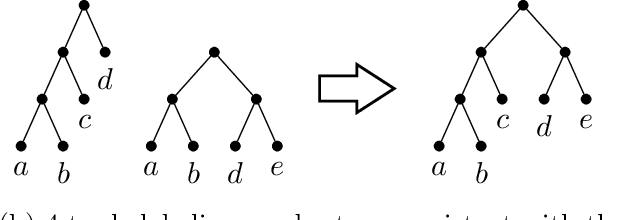
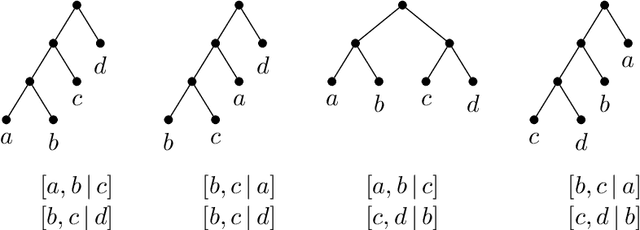
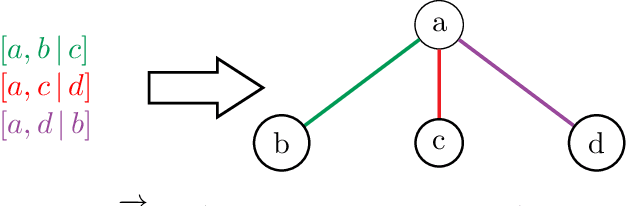
We study the problem of learning a hierarchical tree representation of data from labeled samples, taken from an arbitrary (and possibly adversarial) distribution. Consider a collection of data tuples labeled according to their hierarchical structure. The smallest number of such tuples required in order to be able to accurately label subsequent tuples is of interest for data collection in machine learning. We present optimal sample complexity bounds for this problem in several learning settings, including (agnostic) PAC learning and online learning. Our results are based on tight bounds of the Natarajan and Littlestone dimensions of the associated problem. The corresponding tree classifiers can be constructed efficiently in near-linear time.

HOUDINI: Escaping from Moderately Constrained Saddles

We give the first polynomial time algorithms for escaping from high-dimensional saddle points under a moderate number of constraints. Given gradient access to a smooth function $f \colon \mathbb R^d \to \mathbb R$ we show that (noisy) gradient descent methods can escape from saddle points under a logarithmic number of inequality constraints. This constitutes the first tangible progress (without reliance on NP-oracles or altering the definitions to only account for certain constraints) on the main open question of the breakthrough work of Ge et al. who showed an analogous result for unconstrained and equality-constrained problems. Our results hold for both regular and stochastic gradient descent.

Escaping Saddle Points with Compressed SGD

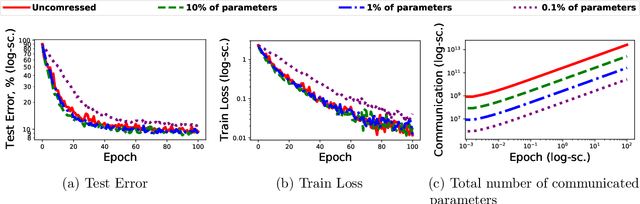
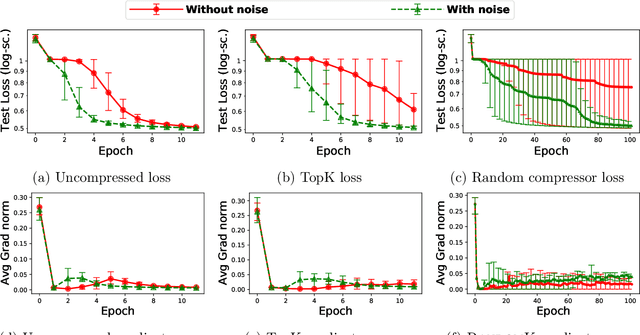
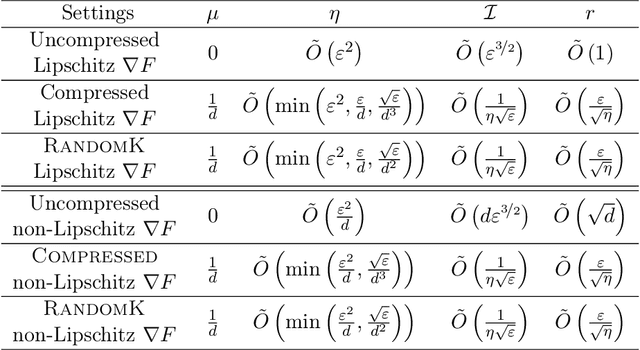
Stochastic gradient descent (SGD) is a prevalent optimization technique for large-scale distributed machine learning. While SGD computation can be efficiently divided between multiple machines, communication typically becomes a bottleneck in the distributed setting. Gradient compression methods can be used to alleviate this problem, and a recent line of work shows that SGD augmented with gradient compression converges to an $\varepsilon$-first-order stationary point. In this paper we extend these results to convergence to an $\varepsilon$-second-order stationary point ($\varepsilon$-SOSP), which is to the best of our knowledge the first result of this type. In addition, we show that, when the stochastic gradient is not Lipschitz, compressed SGD with RandomK compressor converges to an $\varepsilon$-SOSP with the same number of iterations as uncompressed SGD [Jin et al.,2021] (JACM), while improving the total communication by a factor of $\tilde \Theta(\sqrt{d} \varepsilon^{-3/4})$, where $d$ is the dimension of the optimization problem. We present additional results for the cases when the compressor is arbitrary and when the stochastic gradient is Lipschitz.

Objective-Based Hierarchical Clustering of Deep Embedding Vectors

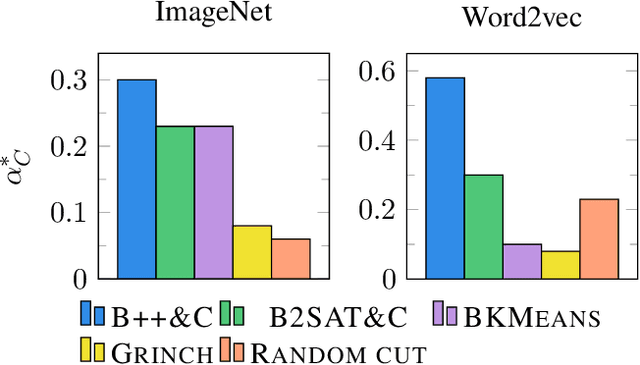
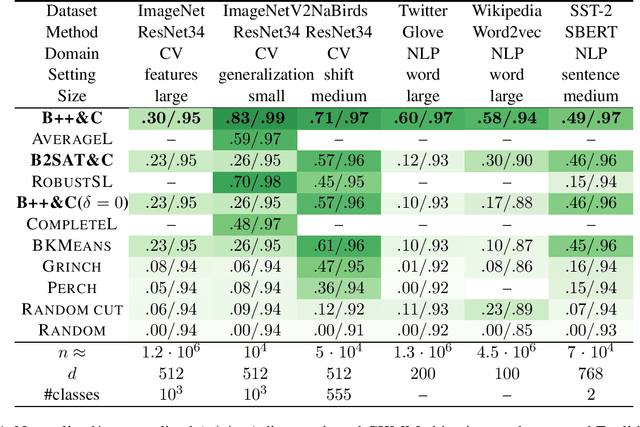
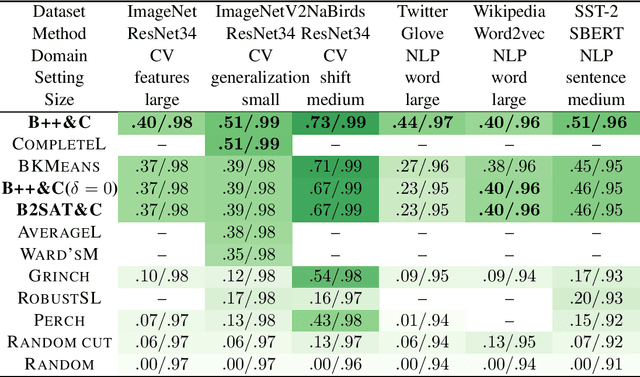
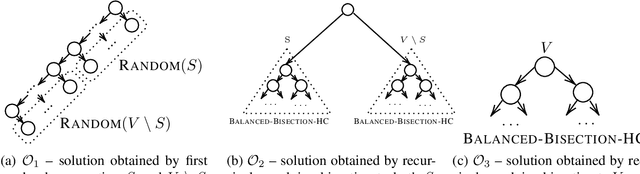
We initiate a comprehensive experimental study of objective-based hierarchical clustering methods on massive datasets consisting of deep embedding vectors from computer vision and NLP applications. This includes a large variety of image embedding (ImageNet, ImageNetV2, NaBirds), word embedding (Twitter, Wikipedia), and sentence embedding (SST-2) vectors from several popular recent models (e.g. ResNet, ResNext, Inception V3, SBERT). Our study includes datasets with up to $4.5$ million entries with embedding dimensions up to $2048$. In order to address the challenge of scaling up hierarchical clustering to such large datasets we propose a new practical hierarchical clustering algorithm B++&C. It gives a 5%/20% improvement on average for the popular Moseley-Wang (MW) / Cohen-Addad et al. (CKMM) objectives (normalized) compared to a wide range of classic methods and recent heuristics. We also introduce a theoretical algorithm B2SAT&C which achieves a $0.74$-approximation for the CKMM objective in polynomial time. This is the first substantial improvement over the trivial $2/3$-approximation achieved by a random binary tree. Prior to this work, the best poly-time approximation of $\approx 2/3 + 0.0004$ was due to Charikar et al. (SODA'19).

"Bring Your Own Greedy"+Max: Near-Optimal $1/2$-Approximations for Submodular Knapsack

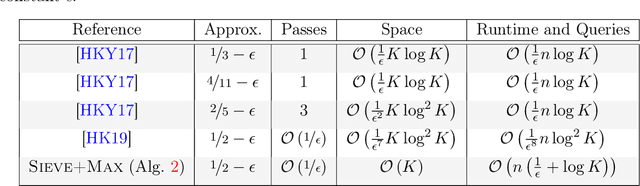
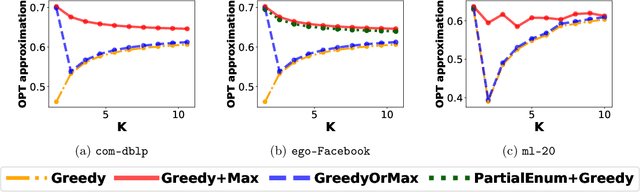
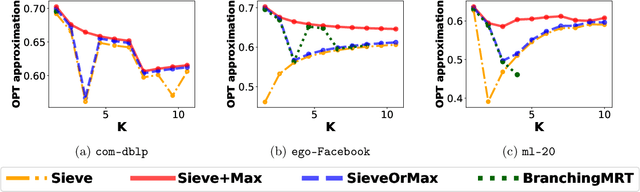
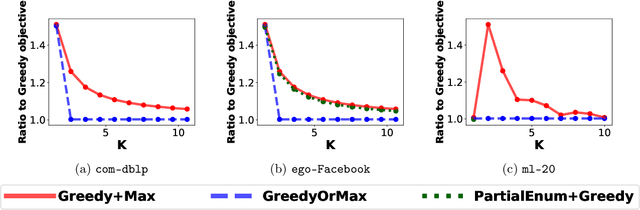
The problem of selecting a small-size representative summary of a large dataset is a cornerstone of machine learning, optimization and data science. Motivated by applications to recommendation systems and other scenarios with query-limited access to vast amounts of data, we propose a new rigorous algorithmic framework for a standard formulation of this problem as a submodular maximization subject to a linear (knapsack) constraint. Our framework is based on augmenting all partial Greedy solutions with the best additional item. It can be instantiated with negligible overhead in any model of computation, which allows the classic \greedy algorithm and its variants to be implemented. We give such instantiations in the offline (Greedy+Max), multi-pass streaming (Sieve+Max) and distributed (Distributed+Max) settings. Our algorithms give ($1/2-\epsilon$)-approximation with most other key parameters of interest being near-optimal. Our analysis is based on a new set of first-order linear differential inequalities and their robust approximate versions. Experiments on typical datasets (movie recommendations, influence maximization) confirm scalability and high quality of solutions obtained via our framework. Instance-specific approximations are typically in the 0.6-0.7 range and frequently beat even the $(1-1/e) \approx 0.63$ worst-case barrier for polynomial-time algorithms.

Adversarially Robust Submodular Maximization under Knapsack Constraints

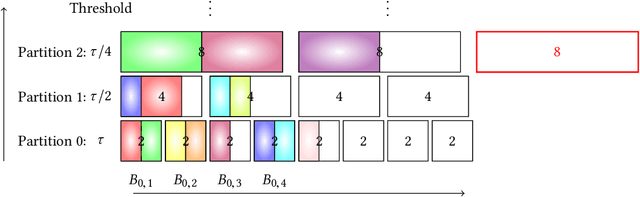
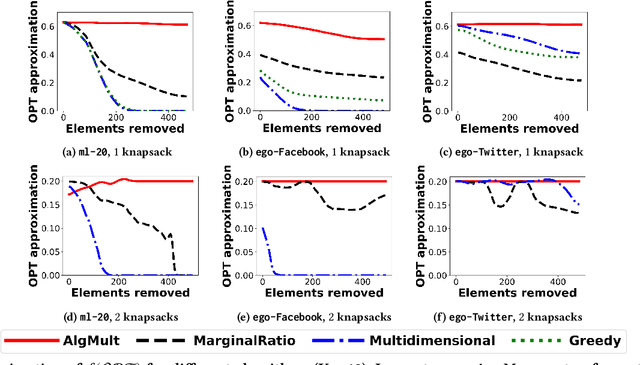
We propose the first adversarially robust algorithm for monotone submodular maximization under single and multiple knapsack constraints with scalable implementations in distributed and streaming settings. For a single knapsack constraint, our algorithm outputs a robust summary of almost optimal (up to polylogarithmic factors) size, from which a constant-factor approximation to the optimal solution can be constructed. For multiple knapsack constraints, our approximation is within a constant-factor of the best known non-robust solution. We evaluate the performance of our algorithms by comparison to natural robustifications of existing non-robust algorithms under two objectives: 1) dominating set for large social network graphs from Facebook and Twitter collected by the Stanford Network Analysis Project (SNAP), 2) movie recommendations on a dataset from MovieLens. Experimental results show that our algorithms give the best objective for a majority of the inputs and show strong performance even compared to offline algorithms that are given the set of removals in advance.