Optimal Sample Complexity of Contrastive Learning

Contrastive learning is a highly successful technique for learning representations of data from labeled tuples, specifying the distance relations within the tuple. We study the sample complexity of contrastive learning, i.e. the minimum number of labeled tuples sufficient for getting high generalization accuracy. We give tight bounds on the sample complexity in a variety of settings, focusing on arbitrary distance functions, both general $\ell_p$-distances, and tree metrics. Our main result is an (almost) optimal bound on the sample complexity of learning $\ell_p$-distances for integer $p$. For any $p \ge 1$ we show that $\tilde \Theta(\min(nd,n^2))$ labeled tuples are necessary and sufficient for learning $d$-dimensional representations of $n$-point datasets. Our results hold for an arbitrary distribution of the input samples and are based on giving the corresponding bounds on the Vapnik-Chervonenkis/Natarajan dimension of the associated problems. We further show that the theoretical bounds on sample complexity obtained via VC/Natarajan dimension can have strong predictive power for experimental results, in contrast with the folklore belief about a substantial gap between the statistical learning theory and the practice of deep learning.

A Unified Characterization of Private Learnability via Graph Theory

We provide a unified framework for characterizing pure and approximate differentially private (DP) learnabiliity. The framework uses the language of graph theory: for a concept class $\mathcal{H}$, we define the contradiction graph $G$ of $\mathcal{H}$. It vertices are realizable datasets, and two datasets $S,S'$ are connected by an edge if they contradict each other (i.e., there is a point $x$ that is labeled differently in $S$ and $S'$). Our main finding is that the combinatorial structure of $G$ is deeply related to learning $\mathcal{H}$ under DP. Learning $\mathcal{H}$ under pure DP is captured by the fractional clique number of $G$. Learning $\mathcal{H}$ under approximate DP is captured by the clique number of $G$. Consequently, we identify graph-theoretic dimensions that characterize DP learnability: the clique dimension and fractional clique dimension. Along the way, we reveal properties of the contradiction graph which may be of independent interest. We also suggest several open questions and directions for future research.

A Theory of PAC Learnability of Partial Concept Classes

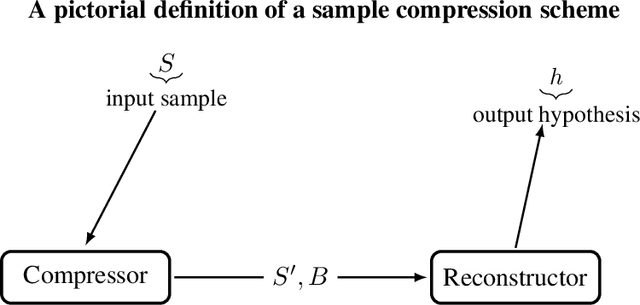
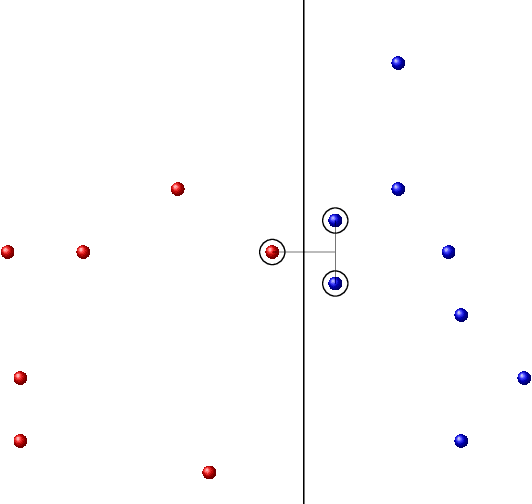
We extend the theory of PAC learning in a way which allows to model a rich variety of learning tasks where the data satisfy special properties that ease the learning process. For example, tasks where the distance of the data from the decision boundary is bounded away from zero. The basic and simple idea is to consider partial concepts: these are functions that can be undefined on certain parts of the space. When learning a partial concept, we assume that the source distribution is supported only on points where the partial concept is defined. This way, one can naturally express assumptions on the data such as lying on a lower dimensional surface or margin conditions. In contrast, it is not at all clear that such assumptions can be expressed by the traditional PAC theory. In fact we exhibit easy-to-learn partial concept classes which provably cannot be captured by the traditional PAC theory. This also resolves a question posed by Attias, Kontorovich, and Mansour 2019. We characterize PAC learnability of partial concept classes and reveal an algorithmic landscape which is fundamentally different than the classical one. For example, in the classical PAC model, learning boils down to Empirical Risk Minimization (ERM). In stark contrast, we show that the ERM principle fails in explaining learnability of partial concept classes. In fact, we demonstrate classes that are incredibly easy to learn, but such that any algorithm that learns them must use an hypothesis space with unbounded VC dimension. We also find that the sample compression conjecture fails in this setting. Thus, this theory features problems that cannot be represented nor solved in the traditional way. We view this as evidence that it might provide insights on the nature of learnability in realistic scenarios which the classical theory fails to explain.

Adversarial Laws of Large Numbers and Optimal Regret in Online Classification

Laws of large numbers guarantee that given a large enough sample from some population, the measure of any fixed sub-population is well-estimated by its frequency in the sample. We study laws of large numbers in sampling processes that can affect the environment they are acting upon and interact with it. Specifically, we consider the sequential sampling model proposed by Ben-Eliezer and Yogev (2020), and characterize the classes which admit a uniform law of large numbers in this model: these are exactly the classes that are \emph{online learnable}. Our characterization may be interpreted as an online analogue to the equivalence between learnability and uniform convergence in statistical (PAC) learning. The sample-complexity bounds we obtain are tight for many parameter regimes, and as an application, we determine the optimal regret bounds in online learning, stated in terms of \emph{Littlestone's dimension}, thus resolving the main open question from Ben-David, P\'al, and Shalev-Shwartz (2009), which was also posed by Rakhlin, Sridharan, and Tewari (2015).

Closure Properties for Private Classification and Online Prediction

Let H be a class of boolean functions and consider acomposed class H' that is derived from H using some arbitrary aggregation rule (for example, H' may be the class of all 3-wise majority votes of functions in H). We upper bound the Littlestone dimension of H' in terms of that of H. The bounds are proved using combinatorial arguments that exploit a connection between the Littlestone dimension and Thresholds. As a corollary, we derive closure properties for online learning and private PAC learning. The derived bounds on the Littlestone dimension exhibit an undesirable super-exponential dependence. For private learning, we prove close to optimal bounds that circumvents this suboptimal dependency. The improved bounds on the sample complexity of private learning are derived algorithmically via transforming a private learner for the original class H to a private learner for the composed class H'. Using the same ideas we show that any (proper or improper) private algorithm that learns a class of functions H in the realizable case (i.e., when the examples are labeled by some function in the class) can be transformed to a private algorithm that learns the class H in the agnostic case.

Boosting Simple Learners

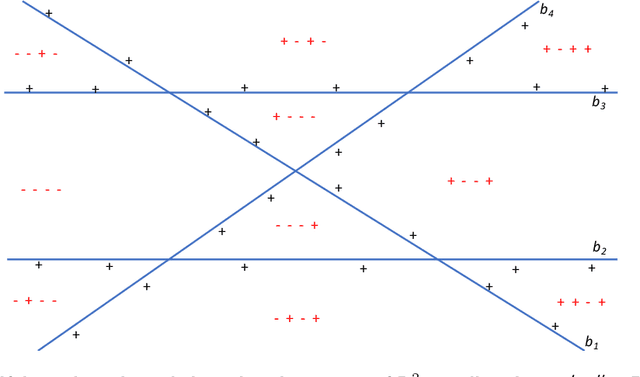
We consider boosting algorithms under the restriction that the weak learners come from a class of bounded VC-dimension. In this setting, we focus on two main questions: (i) \underline{Oracle Complexity:} we show that the restriction on the complexity of the weak learner significantly improves the number of calls to the weak learner. We describe a boosting procedure which makes only~$\tilde O(1/\gamma)$ calls to the weak learner, where $\gamma$ denotes the weak learner's advantage. This circumvents a lower bound of $\Omega(1/\gamma^2)$ due to Freund and Schapire ('95, '12) for the general case. Unlike previous boosting algorithms which aggregate the weak hypotheses by majority votes, our method use more complex aggregation rules, and we show this to be necessary. (ii) \underline{Expressivity:} we consider the question of what can be learned by boosting weak hypotheses of bounded VC-dimension? Towards this end we identify a combinatorial-geometric parameter called the $\gamma$-VC dimension which quantifies the expressivity of a class of weak hypotheses when used as part of a boosting procedure. We explore the limits of the $\gamma$-VC dimension and compute it for well-studied classes such as halfspaces and decision stumps. Along the way, we establish and exploit connections with {\it Discrepancy theory}.

Limits of Private Learning with Access to Public Data

We consider learning problems where the training set consists of two types of examples: private and public. The goal is to design a learning algorithm that satisfies differential privacy only with respect to the private examples. This setting interpolates between private learning (where all examples are private) and classical learning (where all examples are public). We study the limits of learning in this setting in terms of private and public sample complexities. We show that any hypothesis class of VC-dimension $d$ can be agnostically learned up to an excess error of $\alpha$ using only (roughly) $d/\alpha$ public examples and $d/\alpha^2$ private labeled examples. This result holds even when the public examples are unlabeled. This gives a quadratic improvement over the standard $d/\alpha^2$ upper bound on the public sample complexity (where private examples can be ignored altogether if the public examples are labeled). Furthermore, we give a nearly matching lower bound, which we prove via a generic reduction from this setting to the one of private learning without public data.

Private PAC learning implies finite Littlestone dimension

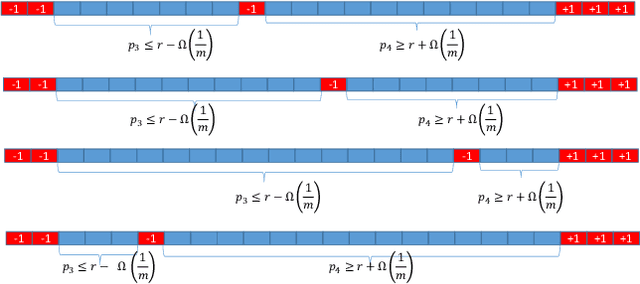
We show that every approximately differentially private learning algorithm (possibly improper) for a class $H$ with Littlestone dimension~$d$ requires $\Omega\bigl(\log^*(d)\bigr)$ examples. As a corollary it follows that the class of thresholds over $\mathbb{N}$ can not be learned in a private manner; this resolves an open question due to [Bun et al. FOCS '15]. We leave as an open question whether every class with a finite Littlestone dimension can be learned by an approximately differentially private algorithm.

Submultiplicative Glivenko-Cantelli and Uniform Convergence of Revenues

In this work we derive a variant of the classic Glivenko-Cantelli Theorem, which asserts uniform convergence of the empirical Cumulative Distribution Function (CDF) to the CDF of the underlying distribution. Our variant allows for tighter convergence bounds for extreme values of the CDF. We apply our bound in the context of revenue learning, which is a well-studied problem in economics and algorithmic game theory. We derive sample-complexity bounds on the uniform convergence rate of the empirical revenues to the true revenues, assuming a bound on the $k$th moment of the valuations, for any (possibly fractional) $k>1$. For uniform convergence in the limit, we give a complete characterization and a zero-one law: if the first moment of the valuations is finite, then uniform convergence almost surely occurs; conversely, if the first moment is infinite, then uniform convergence almost never occurs.

Online Learning with Feedback Graphs: Beyond Bandits

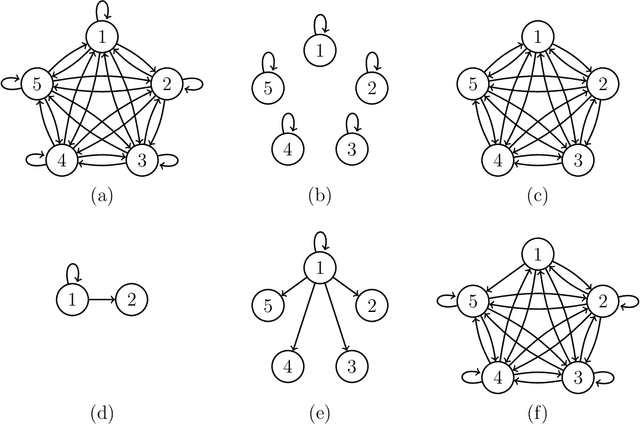
We study a general class of online learning problems where the feedback is specified by a graph. This class includes online prediction with expert advice and the multi-armed bandit problem, but also several learning problems where the online player does not necessarily observe his own loss. We analyze how the structure of the feedback graph controls the inherent difficulty of the induced $T$-round learning problem. Specifically, we show that any feedback graph belongs to one of three classes: strongly observable graphs, weakly observable graphs, and unobservable graphs. We prove that the first class induces learning problems with $\widetilde\Theta(\alpha^{1/2} T^{1/2})$ minimax regret, where $\alpha$ is the independence number of the underlying graph; the second class induces problems with $\widetilde\Theta(\delta^{1/3}T^{2/3})$ minimax regret, where $\delta$ is the domination number of a certain portion of the graph; and the third class induces problems with linear minimax regret. Our results subsume much of the previous work on learning with feedback graphs and reveal new connections to partial monitoring games. We also show how the regret is affected if the graphs are allowed to vary with time.