High-arity PAC learning via exchangeability

We develop a theory of high-arity PAC learning, which is statistical learning in the presence of "structured correlation". In this theory, hypotheses are either graphs, hypergraphs or, more generally, structures in finite relational languages, and i.i.d. sampling is replaced by sampling an induced substructure, producing an exchangeable distribution. We prove a high-arity version of the fundamental theorem of statistical learning by characterizing high-arity (agnostic) PAC learnability in terms of finiteness of a purely combinatorial dimension and in terms of an appropriate version of uniform convergence.

The unstable formula theorem revisited

We first prove that Littlestone classes, those which model theorists call stable, characterize learnability in a new statistical model: a learner in this new setting outputs the same hypothesis, up to measure zero, with probability one, after a uniformly bounded number of revisions. This fills a certain gap in the literature, and sets the stage for an approximation theorem characterizing Littlestone classes in terms of a range of learning models, by analogy to definability of types in model theory. We then give a complete analogue of Shelah's celebrated (and perhaps a priori untranslatable) Unstable Formula Theorem in the learning setting, with algorithmic arguments taking the place of the infinite.

Agnostic Online Learning and Excellent Sets

We use algorithmic methods from online learning to revisit a key idea from the interaction of model theory and combinatorics, the existence of large "indivisible" sets, called "$\epsilon$-excellent," in $k$-edge stable graphs (equivalently, Littlestone classes). These sets arise in the Stable Regularity Lemma, a theorem characterizing the appearance of irregular pairs in Szemer\'edi's celebrated Regularity Lemma. Translating to the language of probability, we find a quite different existence proof for $\epsilon$-excellent sets in Littlestone classes, using regret bounds in online learning. This proof applies to any $\epsilon < {1}/{2}$, compared to $< {1}/{2^{2^k}}$ or so in the original proof. We include a second proof using closure properties and the VC theorem, with other advantages but weaker bounds. As a simple corollary, the Littlestone dimension remains finite under some natural modifications to the definition. A theme in these proofs is the interaction of two abstract notions of majority, arising from measure, and from rank or dimension; we prove that these densely often coincide and that this is characteristic of Littlestone (stable) classes. The last section lists several open problems.

Private PAC learning implies finite Littlestone dimension

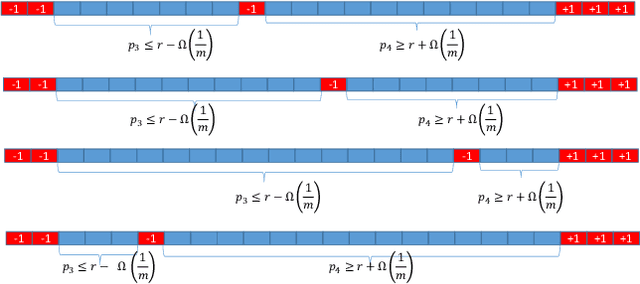
We show that every approximately differentially private learning algorithm (possibly improper) for a class $H$ with Littlestone dimension~$d$ requires $\Omega\bigl(\log^*(d)\bigr)$ examples. As a corollary it follows that the class of thresholds over $\mathbb{N}$ can not be learned in a private manner; this resolves an open question due to [Bun et al. FOCS '15]. We leave as an open question whether every class with a finite Littlestone dimension can be learned by an approximately differentially private algorithm.