Private PAC learning implies finite Littlestone dimension
Paper and Code
Jun 04, 2018
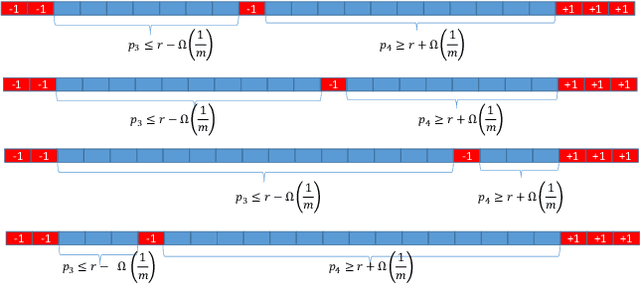
We show that every approximately differentially private learning algorithm (possibly improper) for a class $H$ with Littlestone dimension~$d$ requires $\Omega\bigl(\log^*(d)\bigr)$ examples. As a corollary it follows that the class of thresholds over $\mathbb{N}$ can not be learned in a private manner; this resolves an open question due to [Bun et al. FOCS '15]. We leave as an open question whether every class with a finite Littlestone dimension can be learned by an approximately differentially private algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge