Towards a combinatorial characterization of bounded memory learning

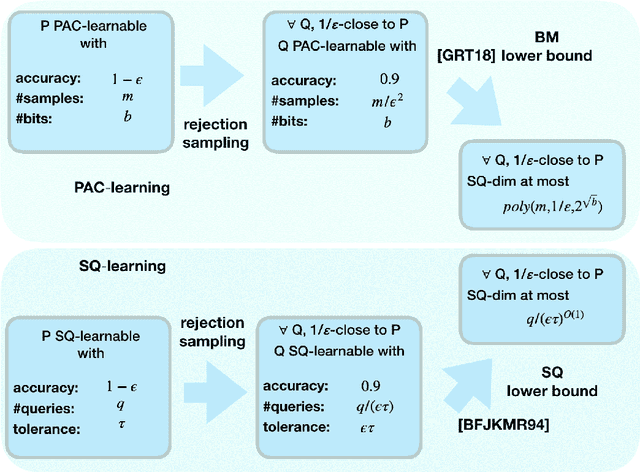
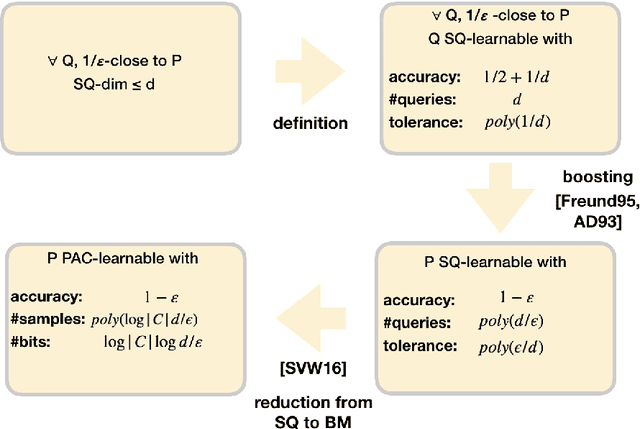
Combinatorial dimensions play an important role in the theory of machine learning. For example, VC dimension characterizes PAC learning, SQ dimension characterizes weak learning with statistical queries, and Littlestone dimension characterizes online learning. In this paper we aim to develop combinatorial dimensions that characterize bounded memory learning. We propose a candidate solution for the case of realizable strong learning under a known distribution, based on the SQ dimension of neighboring distributions. We prove both upper and lower bounds for our candidate solution, that match in some regime of parameters. In this parameter regime there is an equivalence between bounded memory and SQ learning. We conjecture that our characterization holds in a much wider regime of parameters.

Boosting Simple Learners

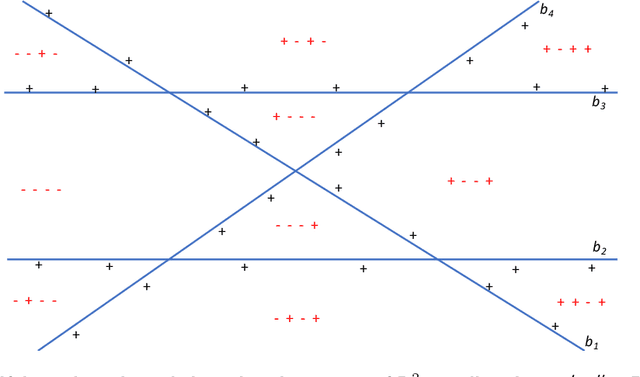
We consider boosting algorithms under the restriction that the weak learners come from a class of bounded VC-dimension. In this setting, we focus on two main questions: (i) \underline{Oracle Complexity:} we show that the restriction on the complexity of the weak learner significantly improves the number of calls to the weak learner. We describe a boosting procedure which makes only~$\tilde O(1/\gamma)$ calls to the weak learner, where $\gamma$ denotes the weak learner's advantage. This circumvents a lower bound of $\Omega(1/\gamma^2)$ due to Freund and Schapire ('95, '12) for the general case. Unlike previous boosting algorithms which aggregate the weak hypotheses by majority votes, our method use more complex aggregation rules, and we show this to be necessary. (ii) \underline{Expressivity:} we consider the question of what can be learned by boosting weak hypotheses of bounded VC-dimension? Towards this end we identify a combinatorial-geometric parameter called the $\gamma$-VC dimension which quantifies the expressivity of a class of weak hypotheses when used as part of a boosting procedure. We explore the limits of the $\gamma$-VC dimension and compute it for well-studied classes such as halfspaces and decision stumps. Along the way, we establish and exploit connections with {\it Discrepancy theory}.

Private Learning Implies Online Learning: An Efficient Reduction

We study the relationship between the notions of differentially private learning and online learning in games. Several recent works have shown that differentially private learning implies online learning, but an open problem of Neel, Roth, and Wu \cite{NeelAaronRoth2018} asks whether this implication is {\it efficient}. Specifically, does an efficient differentially private learner imply an efficient online learner? In this paper we resolve this open question in the context of pure differential privacy. We derive an efficient black-box reduction from differentially private learning to online learning from expert advice.

Learning in Non-convex Games with an Optimization Oracle

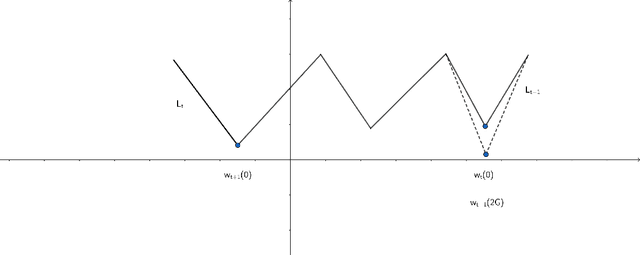
We consider adversarial online learning in a non-convex setting under the assumption that the learner has an access to an offline optimization oracle. In the most general unstructured setting of prediction with expert advice, Hazan and Koren (2015) established an exponential gap demonstrating that online learning can be significantly harder. Interestingly, this gap is eliminated once we assume a convex structure. A natural question which arises is whether the convexity assumption can be dropped. In this work we answer this question in the affirmative. Namely, we show that online learning is computationally equivalent to statistical learning in the Lipschitz-bounded setting. Notably, most deep neural networks satisfy these assumptions. We prove this result by adapting the ubiquitous Follow-The-Perturbed-Leader paradigm of Kalai and Vempala (2004). As an application we demonstrate how the offline oracle enables efficient computation of an equilibrium in non-convex games, that include GAN (generative adversarial networks) as a special case.

Effective Dimension of Exp-concave Optimization

We investigate the role of the effective (a.k.a. statistical) dimension in determining both the statistical and the computational costs associated with exp-concave stochastic minimization. We derive sample complexity bounds that scale with $\frac{d_{\lambda}}{\epsilon}$, where $d_{\lambda}$ is the effective dimension associated with the regularization parameter $\lambda$. These are the first fast rates in this setting that do not exhibit any explicit dependence either on the intrinsic dimension or the $\ell_{2}$-norm of the optimal classifier. We also propose fast preconditioned method that solves the ERM problem in time $\tilde{O} \left(\min \left \{\frac{\lambda'}{\lambda} \left( nnz(A)+d_{\lambda'}^{2}d\right) :~\lambda' \ge \lambda \right \} \right)$, where $nnz(A)$ is the number of nonzero entries in the data. Our analysis emphasizes interesting connections between leverage scores, algorithmic stability and regularization. In particular, our algorithm involves a novel technique for optimizing a tradeoff between oracle complexity and effective dimension. All of our results extend to the kernel setting.

Smooth Sensitivity Based Approach for Differentially Private Principal Component Analysis

Currently known methods for this task either employ the computationally intensive \emph{exponential mechanism} or require an access to the covariance matrix, and therefore fail to utilize potential sparsity of the data. The problem of designing simpler and more efficient methods for this task has been raised as an open problem in \cite{kapralov2013differentially}. In this paper we address this problem by employing the output perturbation mechanism. Despite being arguably the simplest and most straightforward technique, it has been overlooked due to the large \emph{global sensitivity} associated with publishing the leading eigenvector. We tackle this issue by adopting a \emph{smooth sensitivity} based approach, which allows us to establish differential privacy (in a worst-case manner) and near-optimal sample complexity results under eigengap assumption. We consider both the pure and the approximate notions of differential privacy, and demonstrate a tradeoff between privacy level and sample complexity. We conclude by suggesting how our results can be extended to related problems.

Fast Rates for Empirical Risk Minimization of Strict Saddle Problems

We derive bounds on the sample complexity of empirical risk minimization (ERM) in the context of minimizing non-convex risks that admit the strict saddle property. Recent progress in non-convex optimization has yielded efficient algorithms for minimizing such functions. Our results imply that these efficient algorithms are statistically stable and also generalize well. In particular, we derive fast rates which resemble the bounds that are often attained in the strongly convex setting. We specify our bounds to Principal Component Analysis and Independent Component Analysis. Our results and techniques may pave the way for statistical analyses of additional strict saddle problems.

Average Stability is Invariant to Data Preconditioning. Implications to Exp-concave Empirical Risk Minimization

We show that the average stability notion introduced by \cite{kearns1999algorithmic, bousquet2002stability} is invariant to data preconditioning, for a wide class of generalized linear models that includes most of the known exp-concave losses. In other words, when analyzing the stability rate of a given algorithm, we may assume the optimal preconditioning of the data. This implies that, at least from a statistical perspective, explicit regularization is not required in order to compensate for ill-conditioned data, which stands in contrast to a widely common approach that includes a regularization for analyzing the sample complexity of generalized linear models. Several important implications of our findings include: a) We demonstrate that the excess risk of empirical risk minimization (ERM) is controlled by the preconditioned stability rate. This immediately yields a relatively short and elegant proof for the fast rates attained by ERM in our context. b) We strengthen the recent bounds of \cite{hardt2015train} on the stability rate of the Stochastic Gradient Descent algorithm.

Subspace Learning with Partial Information

The goal of subspace learning is to find a $k$-dimensional subspace of $\mathbb{R}^d$, such that the expected squared distance between instance vectors and the subspace is as small as possible. In this paper we study subspace learning in a partial information setting, in which the learner can only observe $r \le d$ attributes from each instance vector. We propose several efficient algorithms for this task, and analyze their sample complexity

Solving Ridge Regression using Sketched Preconditioned SVRG

We develop a novel preconditioning method for ridge regression, based on recent linear sketching methods. By equipping Stochastic Variance Reduced Gradient (SVRG) with this preconditioning process, we obtain a significant speed-up relative to fast stochastic methods such as SVRG, SDCA and SAG.