DeepCut: Unsupervised Segmentation using Graph Neural Networks Clustering

Image segmentation is a fundamental task in computer vision. Data annotation for training supervised methods can be labor-intensive, motivating unsupervised methods. Some existing approaches extract deep features from pre-trained networks and build a graph to apply classical clustering methods (e.g., $k$-means and normalized-cuts) as a post-processing stage. These techniques reduce the high-dimensional information encoded in the features to pair-wise scalar affinities. In this work, we replace classical clustering algorithms with a lightweight Graph Neural Network (GNN) trained to achieve the same clustering objective function. However, in contrast to existing approaches, we feed the GNN not only the pair-wise affinities between local image features but also the raw features themselves. Maintaining this connection between the raw feature and the clustering goal allows to perform part semantic segmentation implicitly, without requiring additional post-processing steps. We demonstrate how classical clustering objectives can be formulated as self-supervised loss functions for training our image segmentation GNN. Additionally, we use the Correlation-Clustering (CC) objective to perform clustering without defining the number of clusters ($k$-less clustering). We apply the proposed method for object localization, segmentation, and semantic part segmentation tasks, surpassing state-of-the-art performance on multiple benchmarks.

Deep Unfolding with Normalizing Flow Priors for Inverse Problems

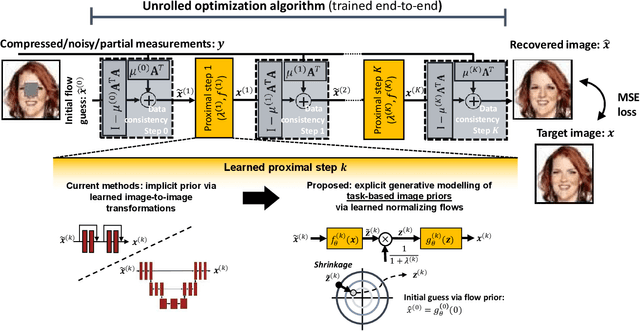
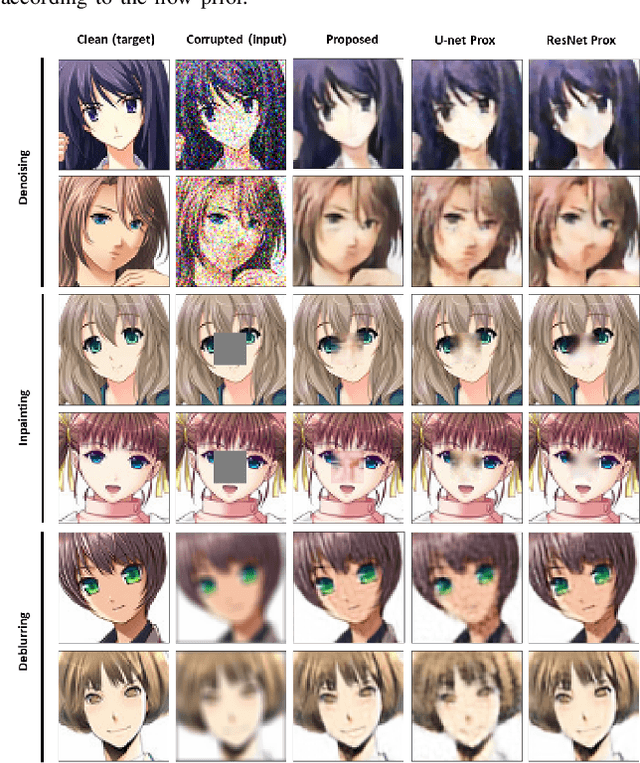
Many application domains, spanning from computational photography to medical imaging, require recovery of high-fidelity images from noisy, incomplete or partial/compressed measurements. State of the art methods for solving these inverse problems combine deep learning with iterative model-based solvers, a concept known as deep algorithm unfolding. By combining a-priori knowledge of the forward measurement model with learned (proximal) mappings based on deep networks, these methods yield solutions that are both physically feasible (data-consistent) and perceptually plausible. However, current proximal mappings only implicitly learn such image priors. In this paper, we propose to make these image priors fully explicit by embedding deep generative models in the form of normalizing flows within the unfolded proximal gradient algorithm. We demonstrate that the proposed method outperforms competitive baselines on various image recovery tasks, spanning from image denoising to inpainting and deblurring.

Subspace Learning with Partial Information

The goal of subspace learning is to find a $k$-dimensional subspace of $\mathbb{R}^d$, such that the expected squared distance between instance vectors and the subspace is as small as possible. In this paper we study subspace learning in a partial information setting, in which the learner can only observe $r \le d$ attributes from each instance vector. We propose several efficient algorithms for this task, and analyze their sample complexity

C-HiLasso: A Collaborative Hierarchical Sparse Modeling Framework

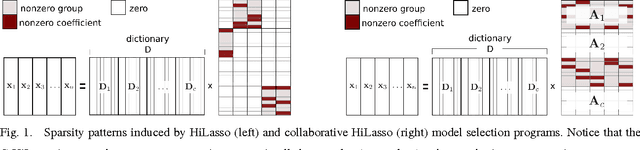
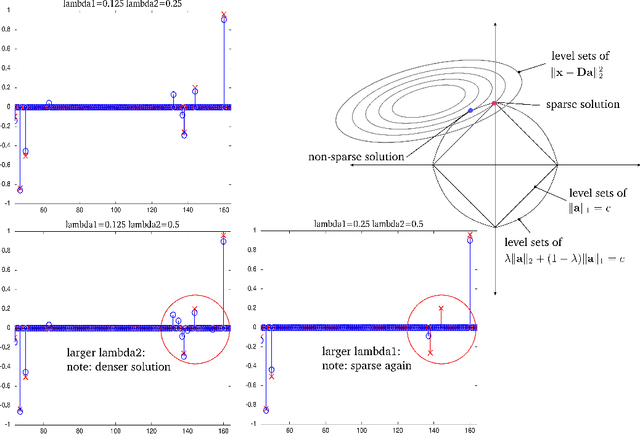
Sparse modeling is a powerful framework for data analysis and processing. Traditionally, encoding in this framework is performed by solving an L1-regularized linear regression problem, commonly referred to as Lasso or Basis Pursuit. In this work we combine the sparsity-inducing property of the Lasso model at the individual feature level, with the block-sparsity property of the Group Lasso model, where sparse groups of features are jointly encoded, obtaining a sparsity pattern hierarchically structured. This results in the Hierarchical Lasso (HiLasso), which shows important practical modeling advantages. We then extend this approach to the collaborative case, where a set of simultaneously coded signals share the same sparsity pattern at the higher (group) level, but not necessarily at the lower (inside the group) level, obtaining the collaborative HiLasso model (C-HiLasso). Such signals then share the same active groups, or classes, but not necessarily the same active set. This model is very well suited for applications such as source identification and separation. An efficient optimization procedure, which guarantees convergence to the global optimum, is developed for these new models. The underlying presentation of the new framework and optimization approach is complemented with experimental examples and theoretical results regarding recovery guarantees for the proposed models.