C-HiLasso: A Collaborative Hierarchical Sparse Modeling Framework
Paper and Code
Mar 04, 2011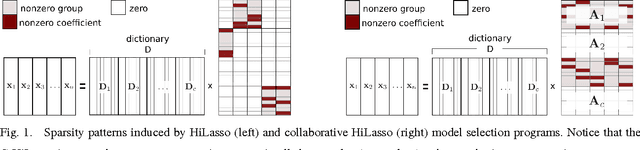
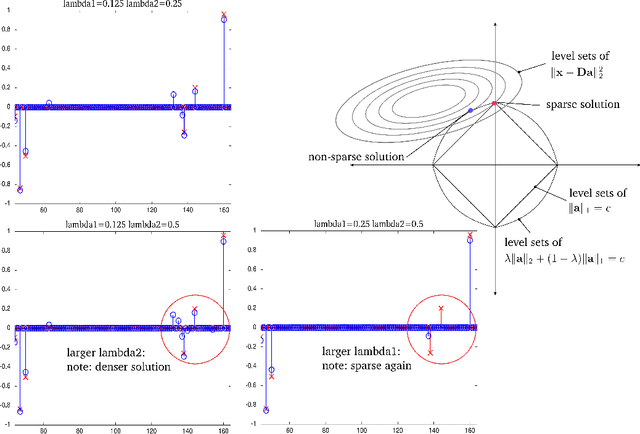
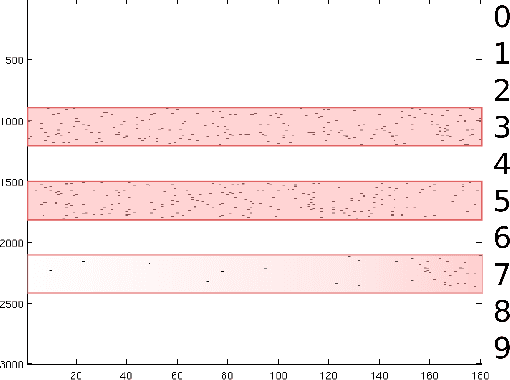
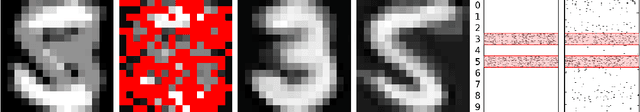
Sparse modeling is a powerful framework for data analysis and processing. Traditionally, encoding in this framework is performed by solving an L1-regularized linear regression problem, commonly referred to as Lasso or Basis Pursuit. In this work we combine the sparsity-inducing property of the Lasso model at the individual feature level, with the block-sparsity property of the Group Lasso model, where sparse groups of features are jointly encoded, obtaining a sparsity pattern hierarchically structured. This results in the Hierarchical Lasso (HiLasso), which shows important practical modeling advantages. We then extend this approach to the collaborative case, where a set of simultaneously coded signals share the same sparsity pattern at the higher (group) level, but not necessarily at the lower (inside the group) level, obtaining the collaborative HiLasso model (C-HiLasso). Such signals then share the same active groups, or classes, but not necessarily the same active set. This model is very well suited for applications such as source identification and separation. An efficient optimization procedure, which guarantees convergence to the global optimum, is developed for these new models. The underlying presentation of the new framework and optimization approach is complemented with experimental examples and theoretical results regarding recovery guarantees for the proposed models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge