Improving OCR using internal document redundancy

Current OCR systems are based on deep learning models trained on large amounts of data. Although they have shown some ability to generalize to unseen data, especially in detection tasks, they can struggle with recognizing low-quality data. This is particularly evident for printed documents, where intra-domain data variability is typically low, but inter-domain data variability is high. In that context, current OCR methods do not fully exploit each document's redundancy. We propose an unsupervised method by leveraging the redundancy of character shapes within a document to correct imperfect outputs of a given OCR system and suggest better clustering. To this aim, we introduce an extended Gaussian Mixture Model (GMM) by alternating an Expectation-Maximization (EM) algorithm with an intra-cluster realignment process and normality statistical testing. We demonstrate improvements in documents with various levels of degradation, including recovered Uruguayan military archives and 17th to mid-20th century European newspapers.

An MDL framework for sparse coding and dictionary learning

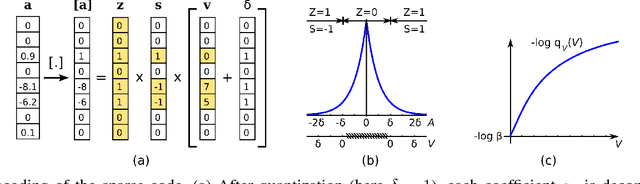
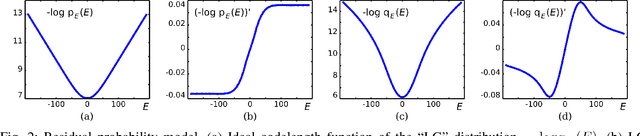
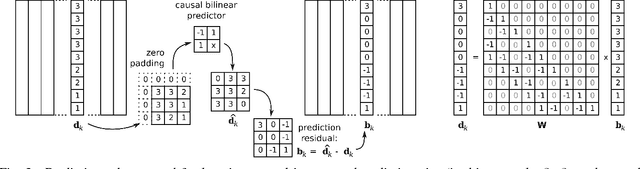
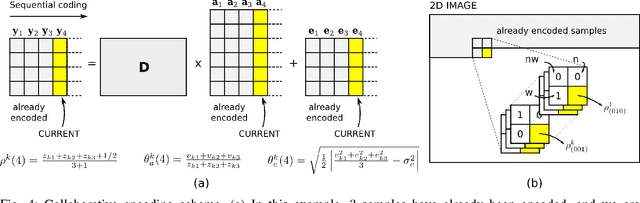
The power of sparse signal modeling with learned over-complete dictionaries has been demonstrated in a variety of applications and fields, from signal processing to statistical inference and machine learning. However, the statistical properties of these models, such as under-fitting or over-fitting given sets of data, are still not well characterized in the literature. As a result, the success of sparse modeling depends on hand-tuning critical parameters for each data and application. This work aims at addressing this by providing a practical and objective characterization of sparse models by means of the Minimum Description Length (MDL) principle -- a well established information-theoretic approach to model selection in statistical inference. The resulting framework derives a family of efficient sparse coding and dictionary learning algorithms which, by virtue of the MDL principle, are completely parameter free. Furthermore, such framework allows to incorporate additional prior information to existing models, such as Markovian dependencies, or to define completely new problem formulations, including in the matrix analysis area, in a natural way. These virtues will be demonstrated with parameter-free algorithms for the classic image denoising and classification problems, and for low-rank matrix recovery in video applications.

Low-rank data modeling via the Minimum Description Length principle

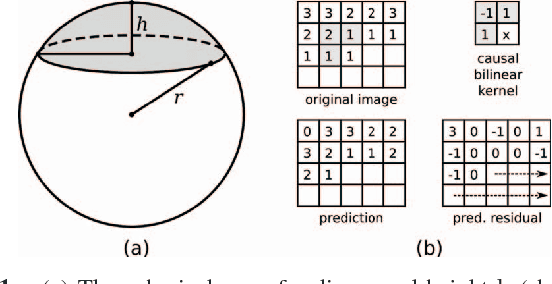
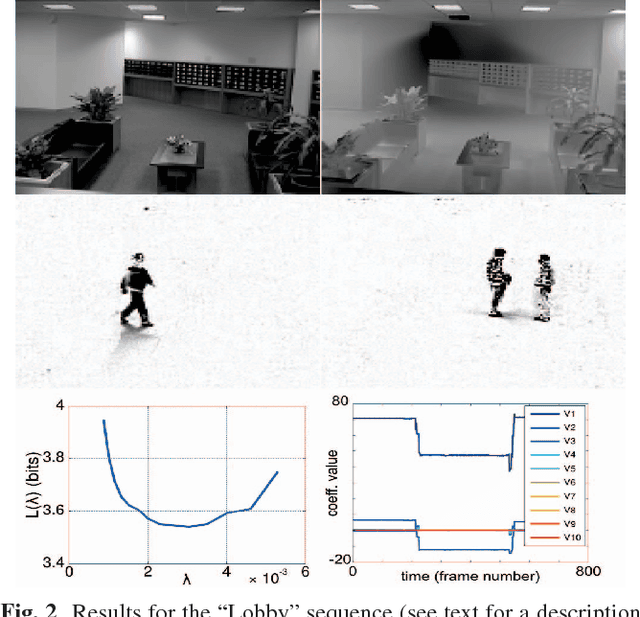
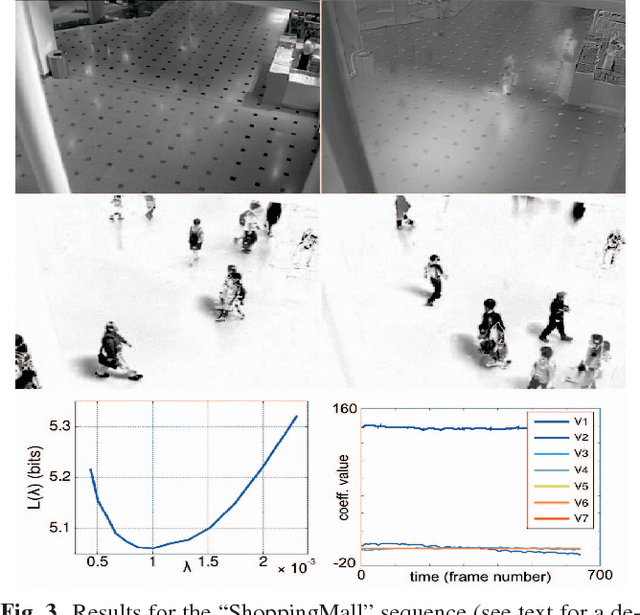
Robust low-rank matrix estimation is a topic of increasing interest, with promising applications in a variety of fields, from computer vision to data mining and recommender systems. Recent theoretical results establish the ability of such data models to recover the true underlying low-rank matrix when a large portion of the measured matrix is either missing or arbitrarily corrupted. However, if low rank is not a hypothesis about the true nature of the data, but a device for extracting regularity from it, no current guidelines exist for choosing the rank of the estimated matrix. In this work we address this problem by means of the Minimum Description Length (MDL) principle -- a well established information-theoretic approach to statistical inference -- as a guideline for selecting a model for the data at hand. We demonstrate the practical usefulness of our formal approach with results for complex background extraction in video sequences.

C-HiLasso: A Collaborative Hierarchical Sparse Modeling Framework

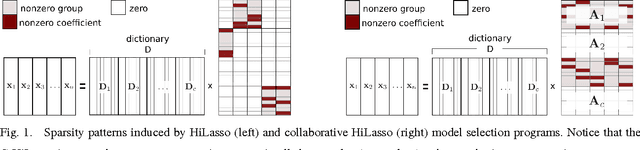
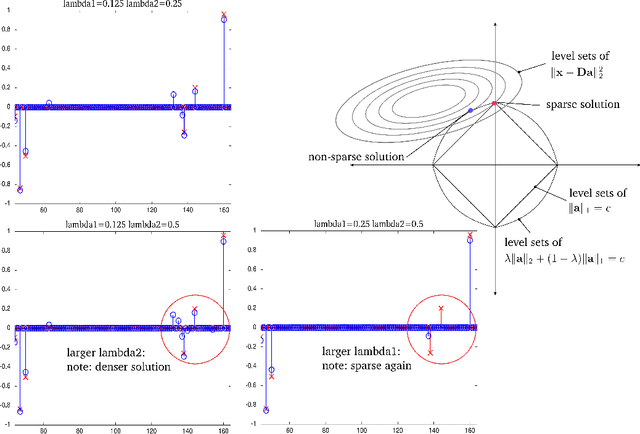
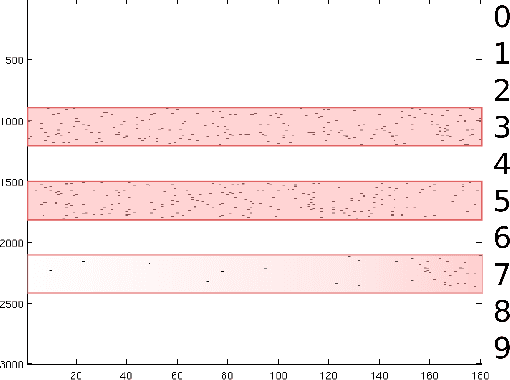
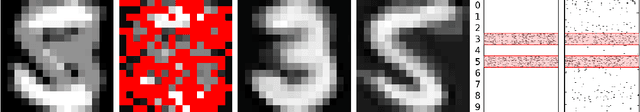
Sparse modeling is a powerful framework for data analysis and processing. Traditionally, encoding in this framework is performed by solving an L1-regularized linear regression problem, commonly referred to as Lasso or Basis Pursuit. In this work we combine the sparsity-inducing property of the Lasso model at the individual feature level, with the block-sparsity property of the Group Lasso model, where sparse groups of features are jointly encoded, obtaining a sparsity pattern hierarchically structured. This results in the Hierarchical Lasso (HiLasso), which shows important practical modeling advantages. We then extend this approach to the collaborative case, where a set of simultaneously coded signals share the same sparsity pattern at the higher (group) level, but not necessarily at the lower (inside the group) level, obtaining the collaborative HiLasso model (C-HiLasso). Such signals then share the same active groups, or classes, but not necessarily the same active set. This model is very well suited for applications such as source identification and separation. An efficient optimization procedure, which guarantees convergence to the global optimum, is developed for these new models. The underlying presentation of the new framework and optimization approach is complemented with experimental examples and theoretical results regarding recovery guarantees for the proposed models.