An MDL framework for sparse coding and dictionary learning

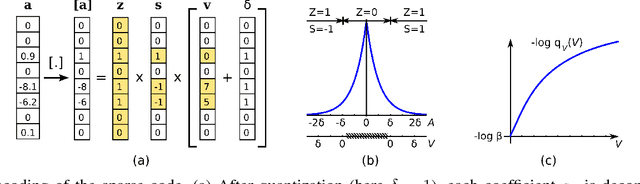
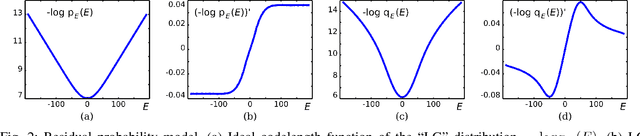
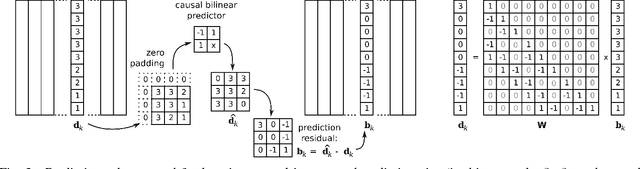
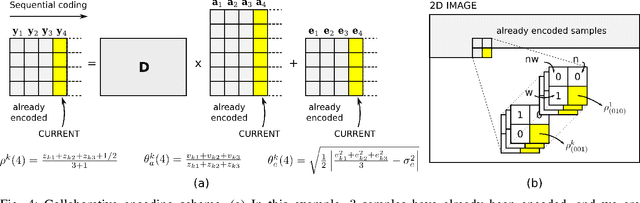
The power of sparse signal modeling with learned over-complete dictionaries has been demonstrated in a variety of applications and fields, from signal processing to statistical inference and machine learning. However, the statistical properties of these models, such as under-fitting or over-fitting given sets of data, are still not well characterized in the literature. As a result, the success of sparse modeling depends on hand-tuning critical parameters for each data and application. This work aims at addressing this by providing a practical and objective characterization of sparse models by means of the Minimum Description Length (MDL) principle -- a well established information-theoretic approach to model selection in statistical inference. The resulting framework derives a family of efficient sparse coding and dictionary learning algorithms which, by virtue of the MDL principle, are completely parameter free. Furthermore, such framework allows to incorporate additional prior information to existing models, such as Markovian dependencies, or to define completely new problem formulations, including in the matrix analysis area, in a natural way. These virtues will be demonstrated with parameter-free algorithms for the classic image denoising and classification problems, and for low-rank matrix recovery in video applications.