Low-rank data modeling via the Minimum Description Length principle
Paper and Code
Sep 28, 2011
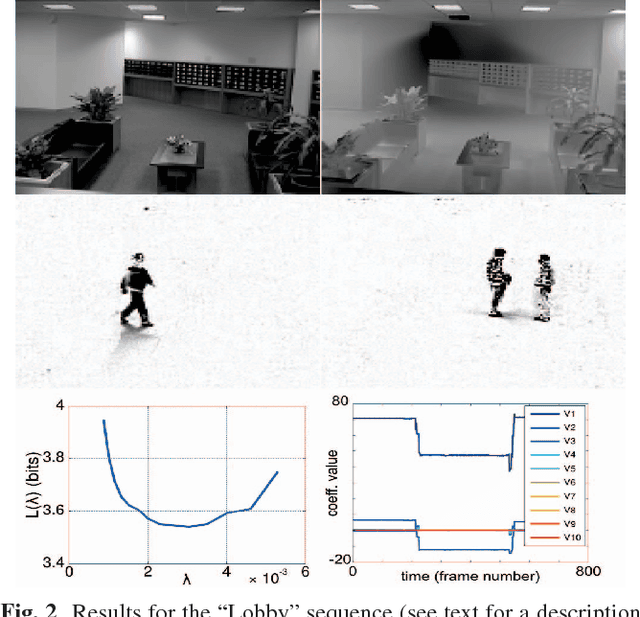
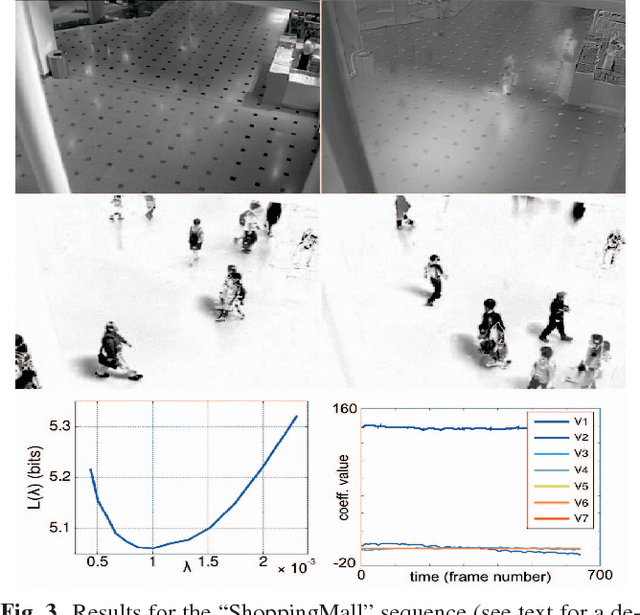
Robust low-rank matrix estimation is a topic of increasing interest, with promising applications in a variety of fields, from computer vision to data mining and recommender systems. Recent theoretical results establish the ability of such data models to recover the true underlying low-rank matrix when a large portion of the measured matrix is either missing or arbitrarily corrupted. However, if low rank is not a hypothesis about the true nature of the data, but a device for extracting regularity from it, no current guidelines exist for choosing the rank of the estimated matrix. In this work we address this problem by means of the Minimum Description Length (MDL) principle -- a well established information-theoretic approach to statistical inference -- as a guideline for selecting a model for the data at hand. We demonstrate the practical usefulness of our formal approach with results for complex background extraction in video sequences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge