Hans van Gorp
Deep Sylvester Posterior Inference for Adaptive Compressed Sensing in Ultrasound Imaging
Jan 07, 2025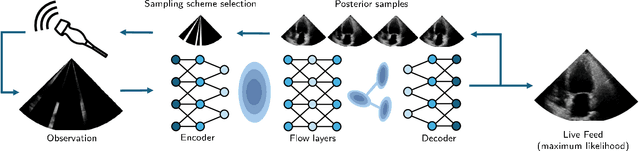
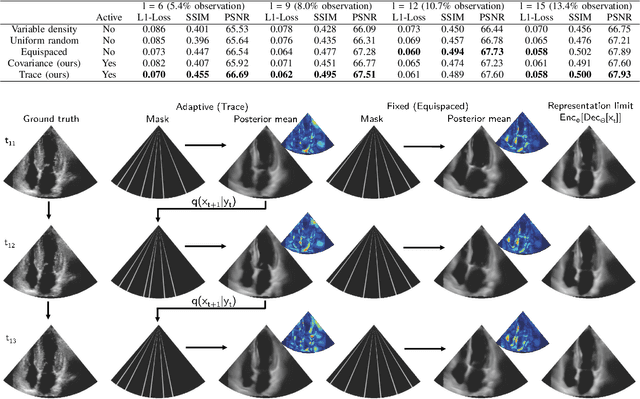
Abstract:Ultrasound images are commonly formed by sequential acquisition of beam-steered scan-lines. Minimizing the number of required scan-lines can significantly enhance frame rate, field of view, energy efficiency, and data transfer speeds. Existing approaches typically use static subsampling schemes in combination with sparsity-based or, more recently, deep-learning-based recovery. In this work, we introduce an adaptive subsampling method that maximizes intrinsic information gain in-situ, employing a Sylvester Normalizing Flow encoder to infer an approximate Bayesian posterior under partial observation in real-time. Using the Bayesian posterior and a deep generative model for future observations, we determine the subsampling scheme that maximizes the mutual information between the subsampled observations, and the next frame of the video. We evaluate our approach using the EchoNet cardiac ultrasound video dataset and demonstrate that our active sampling method outperforms competitive baselines, including uniform and variable-density random sampling, as well as equidistantly spaced scan-lines, improving mean absolute reconstruction error by 15%. Moreover, posterior inference and the sampling scheme generation are performed in just 0.015 seconds (66Hz), making it fast enough for real-time 2D ultrasound imaging applications.
Learning Structured Compressed Sensing with Automatic Resource Allocation
Oct 24, 2024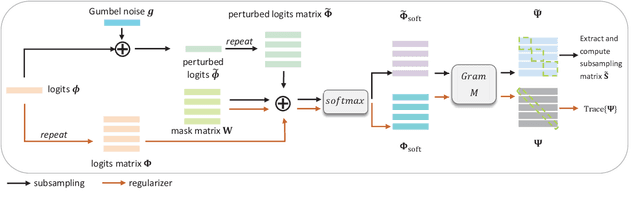
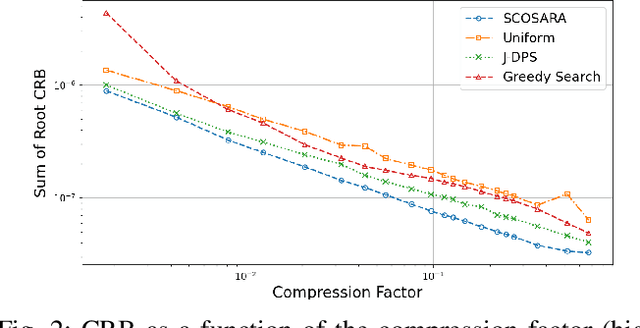
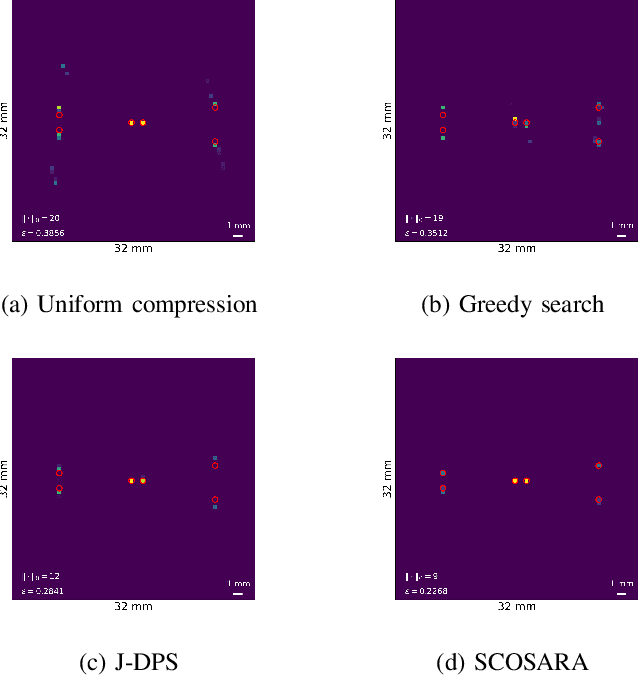
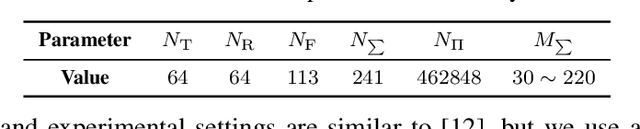
Abstract:Multidimensional data acquisition often requires extensive time and poses significant challenges for hardware and software regarding data storage and processing. Rather than designing a single compression matrix as in conventional compressed sensing, structured compressed sensing yields dimension-specific compression matrices, reducing the number of optimizable parameters. Recent advances in machine learning (ML) have enabled task-based supervised learning of subsampling matrices, albeit at the expense of complex downstream models. Additionally, the sampling resource allocation across dimensions is often determined in advance through heuristics. To address these challenges, we introduce Structured COmpressed Sensing with Automatic Resource Allocation (SCOSARA) with an information theory-based unsupervised learning strategy. SCOSARA adaptively distributes samples across sampling dimensions while maximizing Fisher information content. Using ultrasound localization as a case study, we compare SCOSARA to state-of-the-art ML-based and greedy search algorithms. Simulation results demonstrate that SCOSARA can produce high-quality subsampling matrices that achieve lower Cram\'er-Rao Bound values than the baselines. In addition, SCOSARA outperforms other ML-based algorithms in terms of the number of trainable parameters, computational complexity, and memory requirements while automatically choosing the number of samples per axis.
The Tree of Diffusion Life: Evolutionary Embeddings to Understand the Generation Process of Diffusion Models
Jun 25, 2024Abstract:Diffusion models generate high-quality samples by corrupting data with Gaussian noise and iteratively reconstructing it with deep learning, slowly transforming noisy images into refined outputs. Understanding this data evolution is important for interpretability but is complex due to its high-dimensional evolutionary nature. While traditional dimensionality reduction methods like t-distributed stochastic neighborhood embedding (t-SNE) aid in understanding high-dimensional spaces, they neglect evolutionary structure preservation. Hence, we propose Tree of Diffusion Life (TDL), a method to understand data evolution in the generative process of diffusion models. TDL samples a diffusion model's generative space via instances with varying prompts and employs image encoders to extract semantic meaning from these samples, projecting them to an intermediate space. It employs a novel evolutionary embedding algorithm that explicitly encodes the iterations while preserving the high-dimensional relations, facilitating the visualization of data evolution. This embedding leverages three metrics: a standard t-SNE loss to group semantically similar elements, a displacement loss to group elements from the same iteration step, and an instance alignment loss to align elements of the same instance across iterations. We present rectilinear and radial layouts to represent iterations, enabling comprehensive exploration. We assess various feature extractors and highlight TDL's potential with prominent diffusion models like GLIDE and Stable Diffusion with different prompt sets. TDL simplifies understanding data evolution within diffusion models, offering valuable insights into their functioning.
Deep Unfolding with Normalizing Flow Priors for Inverse Problems
Jul 06, 2021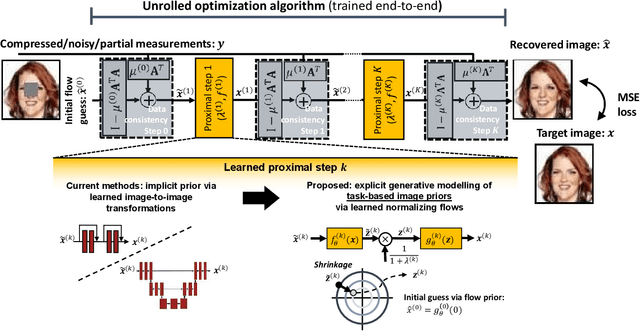


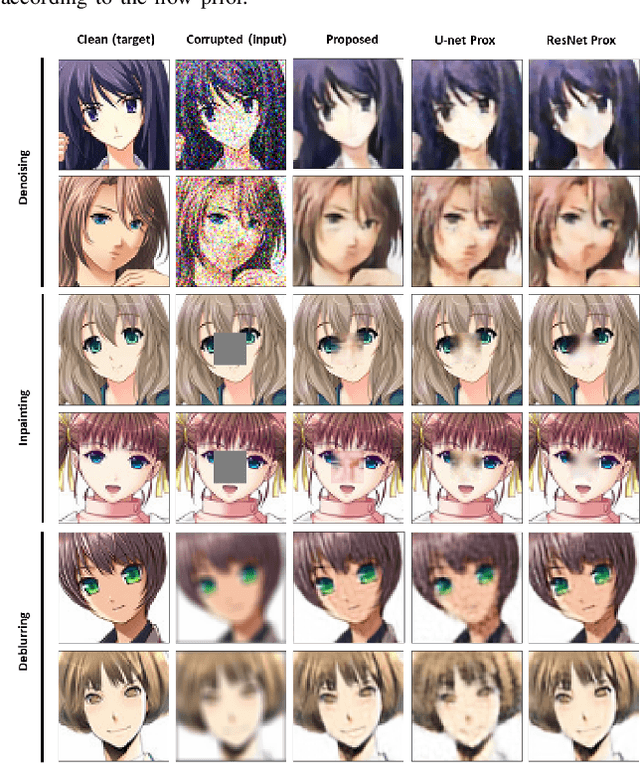
Abstract:Many application domains, spanning from computational photography to medical imaging, require recovery of high-fidelity images from noisy, incomplete or partial/compressed measurements. State of the art methods for solving these inverse problems combine deep learning with iterative model-based solvers, a concept known as deep algorithm unfolding. By combining a-priori knowledge of the forward measurement model with learned (proximal) mappings based on deep networks, these methods yield solutions that are both physically feasible (data-consistent) and perceptually plausible. However, current proximal mappings only implicitly learn such image priors. In this paper, we propose to make these image priors fully explicit by embedding deep generative models in the form of normalizing flows within the unfolded proximal gradient algorithm. We demonstrate that the proposed method outperforms competitive baselines on various image recovery tasks, spanning from image denoising to inpainting and deblurring.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge