Learning Structured Compressed Sensing with Automatic Resource Allocation

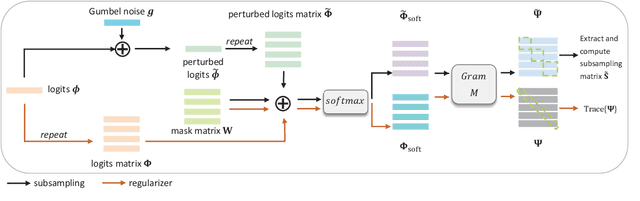
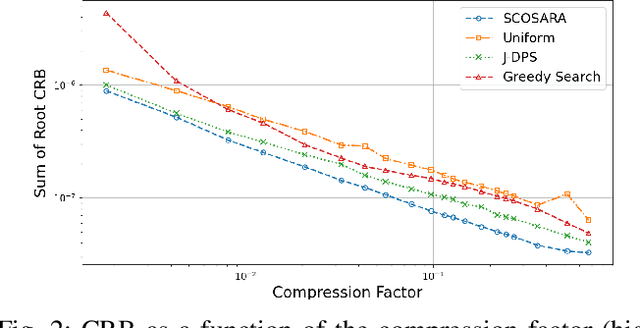
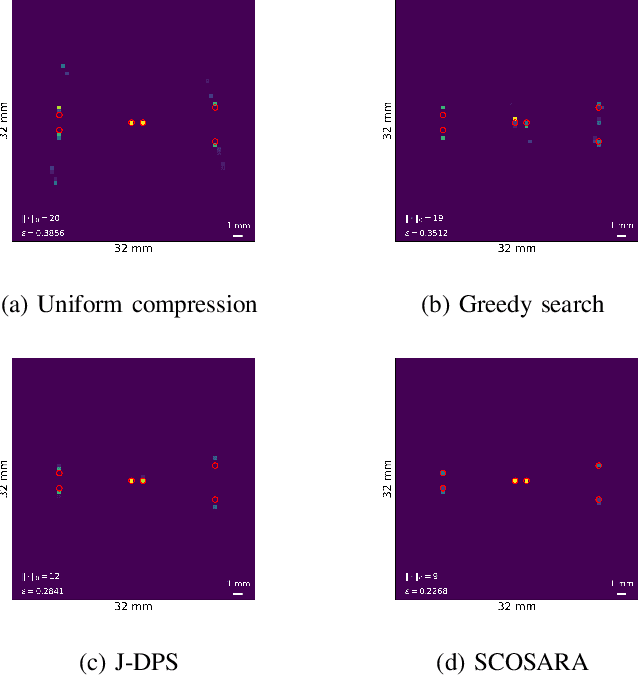
Multidimensional data acquisition often requires extensive time and poses significant challenges for hardware and software regarding data storage and processing. Rather than designing a single compression matrix as in conventional compressed sensing, structured compressed sensing yields dimension-specific compression matrices, reducing the number of optimizable parameters. Recent advances in machine learning (ML) have enabled task-based supervised learning of subsampling matrices, albeit at the expense of complex downstream models. Additionally, the sampling resource allocation across dimensions is often determined in advance through heuristics. To address these challenges, we introduce Structured COmpressed Sensing with Automatic Resource Allocation (SCOSARA) with an information theory-based unsupervised learning strategy. SCOSARA adaptively distributes samples across sampling dimensions while maximizing Fisher information content. Using ultrasound localization as a case study, we compare SCOSARA to state-of-the-art ML-based and greedy search algorithms. Simulation results demonstrate that SCOSARA can produce high-quality subsampling matrices that achieve lower Cram\'er-Rao Bound values than the baselines. In addition, SCOSARA outperforms other ML-based algorithms in terms of the number of trainable parameters, computational complexity, and memory requirements while automatically choosing the number of samples per axis.

SOM-CPC: Unsupervised Contrastive Learning with Self-Organizing Maps for Structured Representations of High-Rate Time Series

Continuous monitoring with an ever-increasing number of sensors has become ubiquitous across many application domains. Acquired data are typically high-dimensional and difficult to interpret, but they are also hypothesized to lie on a lower-dimensional manifold. Many deep learning (DL) models aim to identify this manifold, but do not promote structure nor interpretability. We propose the SOM-CPC model, which jointly optimizes Contrastive Predictive Coding (CPC), and a Self-Organizing Map (SOM) to find such an organized manifold. We address a largely unexplored and challenging set of scenarios comprising high-rate time series, and show on synthetic and real-life medical and audio data that SOM-CPC outperforms strong baseline models that combine DL with SOMs. SOM-CPC has great potential to expose latent patterns in high-rate data streams, and may therefore contribute to a better understanding of many different processes and systems.

A Review of the Gumbel-max Trick and its Extensions for Discrete Stochasticity in Machine Learning

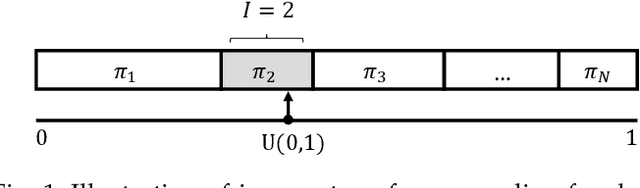
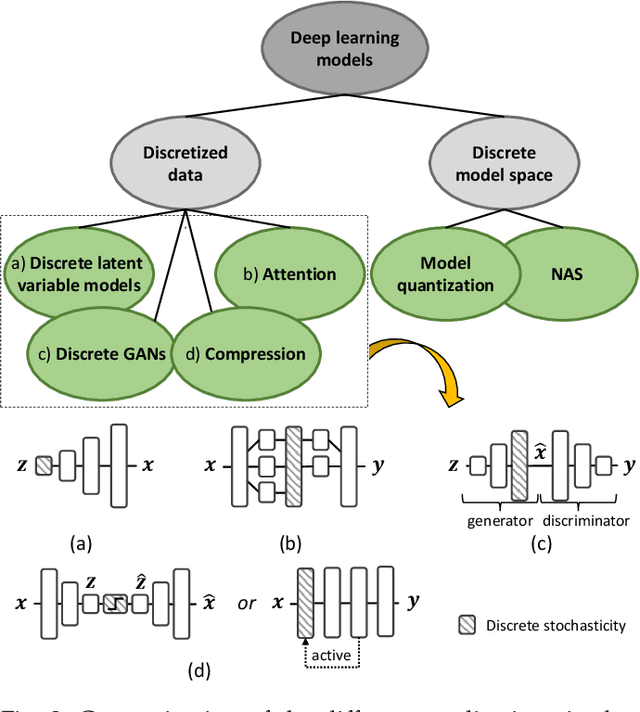
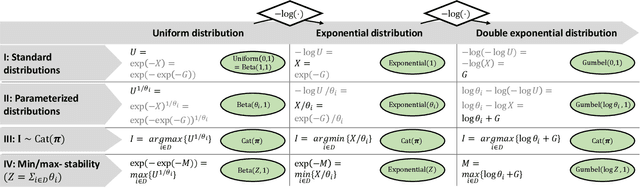
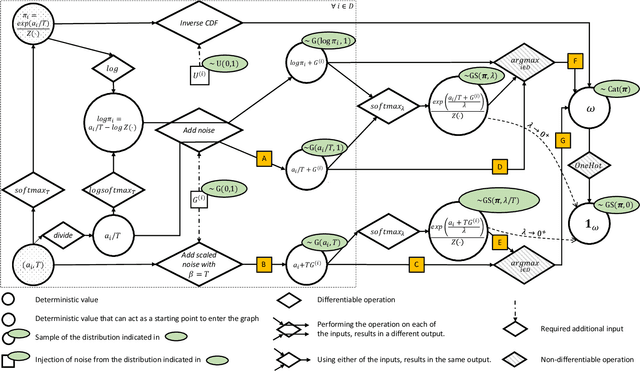
The Gumbel-max trick is a method to draw a sample from a categorical distribution, given by its unnormalized (log-)probabilities. Over the past years, the machine learning community has proposed several extensions of this trick to facilitate, e.g., drawing multiple samples, sampling from structured domains, or gradient estimation for error backpropagation in neural network optimization. The goal of this survey article is to present background about the Gumbel-max trick, and to provide a structured overview of its extensions to ease algorithm selection. Moreover, it presents a comprehensive outline of (machine learning) literature in which Gumbel-based algorithms have been leveraged, reviews commonly-made design choices, and sketches a future perspective.

Dynamic Probabilistic Pruning: A general framework for hardware-constrained pruning at different granularities

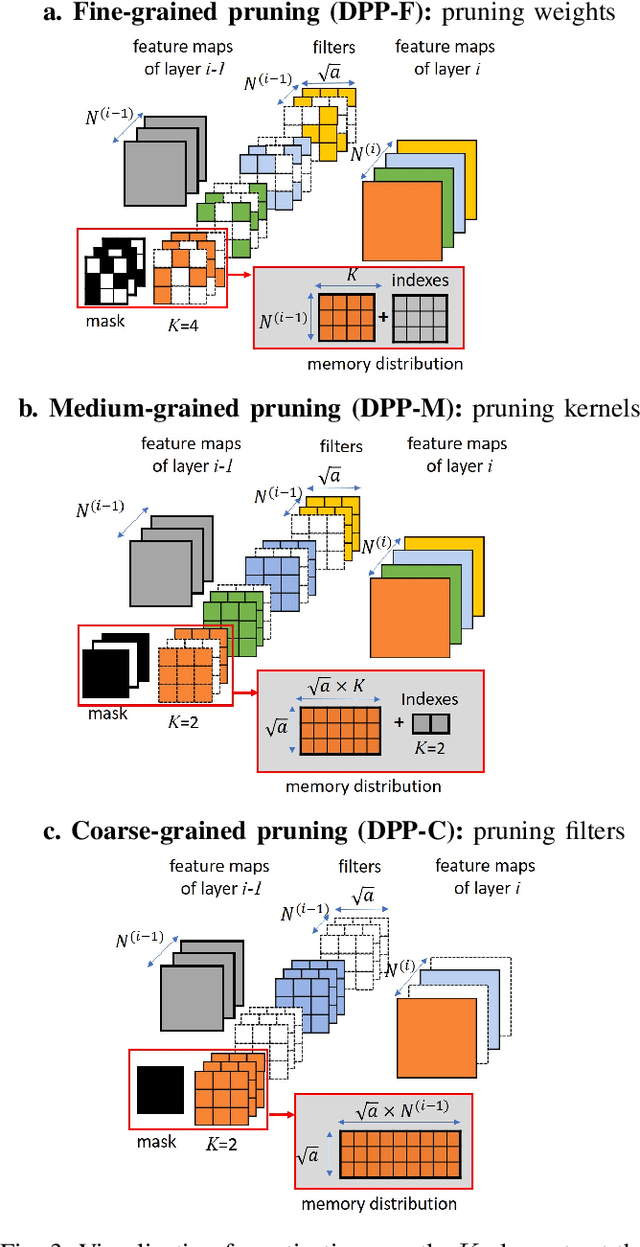
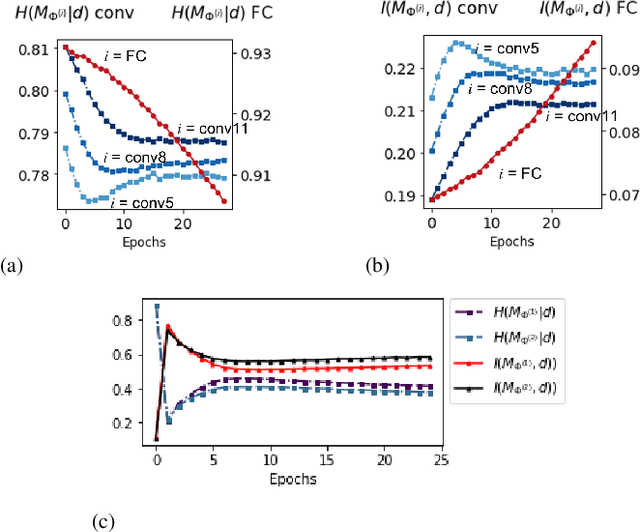
Unstructured neural network pruning algorithms have achieved impressive compression rates. However, the resulting - typically irregular - sparse matrices hamper efficient hardware implementations, leading to additional memory usage and complex control logic that diminishes the benefits of unstructured pruning. This has spurred structured coarse-grained pruning solutions that prune entire filters or even layers, enabling efficient implementation at the expense of reduced flexibility. Here we propose a flexible new pruning mechanism that facilitates pruning at different granularities (weights, kernels, filters/feature maps), while retaining efficient memory organization (e.g. pruning exactly k-out-of-n weights for every output neuron, or pruning exactly k-out-of-n kernels for every feature map). We refer to this algorithm as Dynamic Probabilistic Pruning (DPP). DPP leverages the Gumbel-softmax relaxation for differentiable k-out-of-n sampling, facilitating end-to-end optimization. We show that DPP achieves competitive compression rates and classification accuracy when pruning common deep learning models trained on different benchmark datasets for image classification. Relevantly, the non-magnitude-based nature of DPP allows for joint optimization of pruning and weight quantization in order to even further compress the network, which we show as well. Finally, we propose novel information theoretic metrics that show the confidence and pruning diversity of pruning masks within a layer.

Overfitting for Fun and Profit: Instance-Adaptive Data Compression

Neural data compression has been shown to outperform classical methods in terms of $RD$ performance, with results still improving rapidly. At a high level, neural compression is based on an autoencoder that tries to reconstruct the input instance from a (quantized) latent representation, coupled with a prior that is used to losslessly compress these latents. Due to limitations on model capacity and imperfect optimization and generalization, such models will suboptimally compress test data in general. However, one of the great strengths of learned compression is that if the test-time data distribution is known and relatively low-entropy (e.g. a camera watching a static scene, a dash cam in an autonomous car, etc.), the model can easily be finetuned or adapted to this distribution, leading to improved $RD$ performance. In this paper we take this concept to the extreme, adapting the full model to a single video, and sending model updates (quantized and compressed using a parameter-space prior) along with the latent representation. Unlike previous work, we finetune not only the encoder/latents but the entire model, and - during finetuning - take into account both the effect of model quantization and the additional costs incurred by sending the model updates. We evaluate an image compression model on I-frames (sampled at 2 fps) from videos of the Xiph dataset, and demonstrate that full-model adaptation improves $RD$ performance by ~1 dB, with respect to encoder-only finetuning.

Learning Sampling and Model-Based Signal Recovery for Compressed Sensing MRI

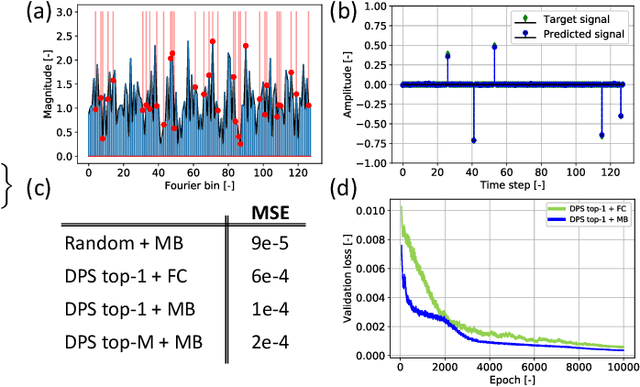
Compressed sensing (CS) MRI relies on adequate undersampling of the k-space to accelerate the acquisition without compromising image quality. Consequently, the design of optimal sampling patterns for these k-space coefficients has received significant attention, with many CS MRI methods exploiting variable-density probability distributions. Realizing that an optimal sampling pattern may depend on the downstream task (e.g. image reconstruction, segmentation, or classification), we here propose joint learning of both task-adaptive k-space sampling and a subsequent model-based proximal-gradient recovery network. The former is enabled through a probabilistic generative model that leverages the Gumbel-softmax relaxation to sample across trainable beliefs while maintaining differentiability. The proposed combination of a highly flexible sampling model and a model-based (sampling-adaptive) image reconstruction network facilitates exploration and efficient training, yielding improved MR image quality compared to other sampling baselines.

Learning Sub-Sampling and Signal Recovery with Applications in Ultrasound Imaging

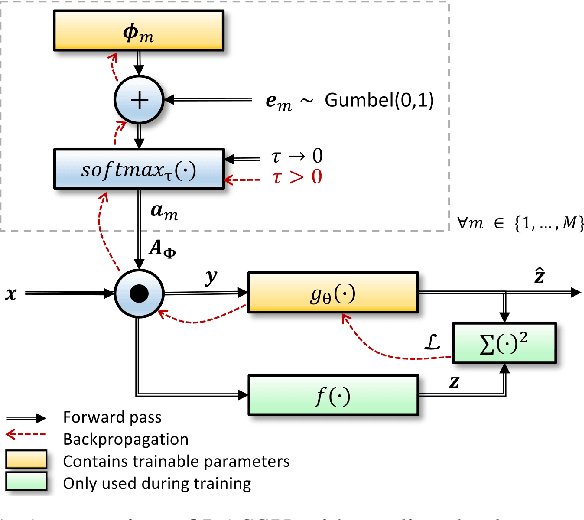
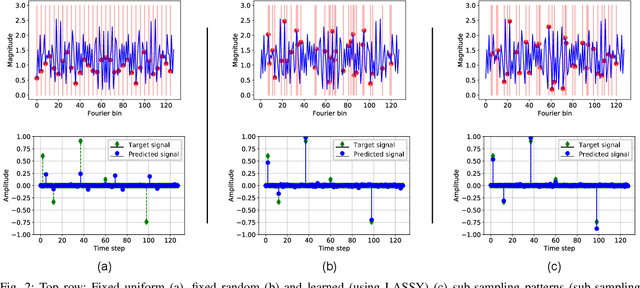
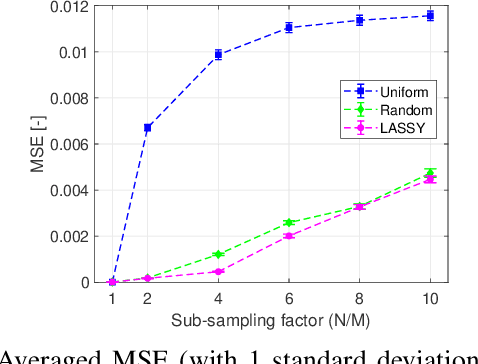
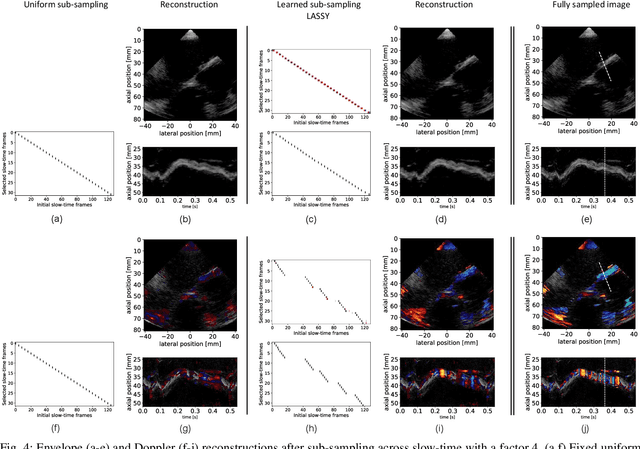
Limitations on bandwidth and power consumption impose strict bounds on data rates of diagnostic imaging systems. Consequently, the design of suitable (i.e. task- and data-aware) compression and reconstruction techniques has attracted considerable attention in recent years. Compressed sensing emerged as a popular framework for sparse signal reconstruction from a small set of compressed measurements. However, typical compressed sensing designs measure a (non)linearly weighted combination of all input signal elements, which poses practical challenges. These designs are also not necessarily task-optimal. In addition, real-time recovery is hampered by the iterative and time-consuming nature of sparse recovery algorithms. Recently, deep learning methods have shown promise for fast recovery from compressed measurements, but the design of adequate and practical sensing strategies remains a challenge. Here, we propose a deep learning solution, termed LASSY (LeArning Sub-Sampling and recoverY), that jointly learns a task-driven sub-sampling pattern and subsequent reconstruction model. The learned sub-sampling patterns are straightforwardly implementable, and based on the task at hand. LASSY's effectiveness is demonstrated in-silico for sparse signal recovery from partial Fourier measurements, and in-vivo for both anatomical-image and motion (Doppler) reconstruction from sub-sampled medical ultrasound imaging data.