Max B. Paulus
Learning to Configure Separators in Branch-and-Cut
Nov 08, 2023Abstract:Cutting planes are crucial in solving mixed integer linear programs (MILP) as they facilitate bound improvements on the optimal solution. Modern MILP solvers rely on a variety of separators to generate a diverse set of cutting planes by invoking the separators frequently during the solving process. This work identifies that MILP solvers can be drastically accelerated by appropriately selecting separators to activate. As the combinatorial separator selection space imposes challenges for machine learning, we learn to separate by proposing a novel data-driven strategy to restrict the selection space and a learning-guided algorithm on the restricted space. Our method predicts instance-aware separator configurations which can dynamically adapt during the solve, effectively accelerating the open source MILP solver SCIP by improving the relative solve time up to 72% and 37% on synthetic and real-world MILP benchmarks. Our work complements recent work on learning to select cutting planes and highlights the importance of separator management.
Learning To Dive In Branch And Bound
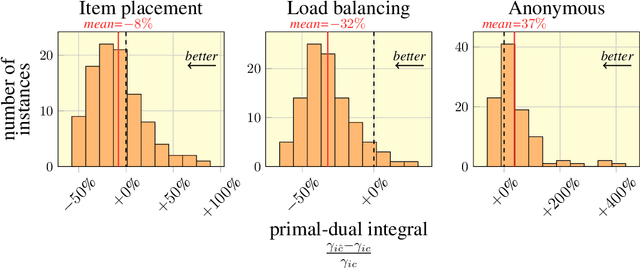
Jan 24, 2023Abstract:Primal heuristics are important for solving mixed integer linear programs, because they find feasible solutions that facilitate branch and bound search. A prominent group of primal heuristics are diving heuristics. They iteratively modify and resolve linear programs to conduct a depth-first search from any node in the search tree. Existing divers rely on generic decision rules that fail to exploit structural commonality between similar problem instances that often arise in practice. Therefore, we propose L2Dive to learn specific diving heuristics with graph neural networks: We train generative models to predict variable assignments and leverage the duality of linear programs to make diving decisions based on the model's predictions. L2Dive is fully integrated into the open-source solver SCIP. We find that L2Dive outperforms standard divers to find better feasible solutions on a range of combinatorial optimization problems. For real-world applications from server load balancing and neural network verification, L2Dive improves the primal-dual integral by up to 7% (35%) on average over a tuned (default) solver baseline and reduces average solving time by 20% (29%).
Learning to Drop Out: An Adversarial Approach to Training Sequence VAEs
Sep 26, 2022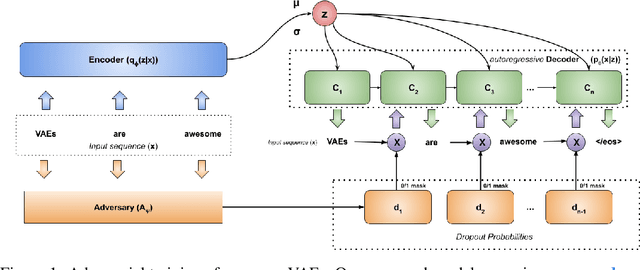
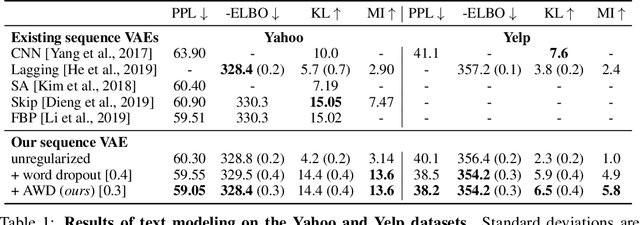
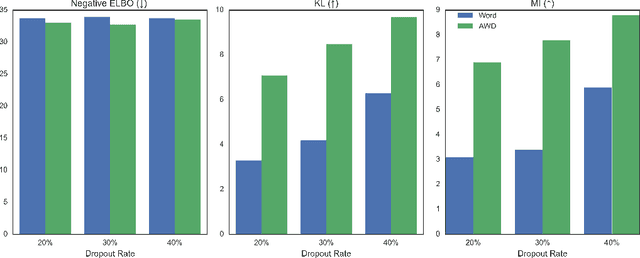

Abstract:In principle, applying variational autoencoders (VAEs) to sequential data offers a method for controlled sequence generation, manipulation, and structured representation learning. However, training sequence VAEs is challenging: autoregressive decoders can often explain the data without utilizing the latent space, known as posterior collapse. To mitigate this, state-of-the-art models weaken the powerful decoder by applying uniformly random dropout to the decoder input. We show theoretically that this removes pointwise mutual information provided by the decoder input, which is compensated for by utilizing the latent space. We then propose an adversarial training strategy to achieve information-based stochastic dropout. Compared to uniform dropout on standard text benchmark datasets, our targeted approach increases both sequence modeling performance and the information captured in the latent space.
Learning To Cut By Looking Ahead: Cutting Plane Selection via Imitation Learning
Jun 27, 2022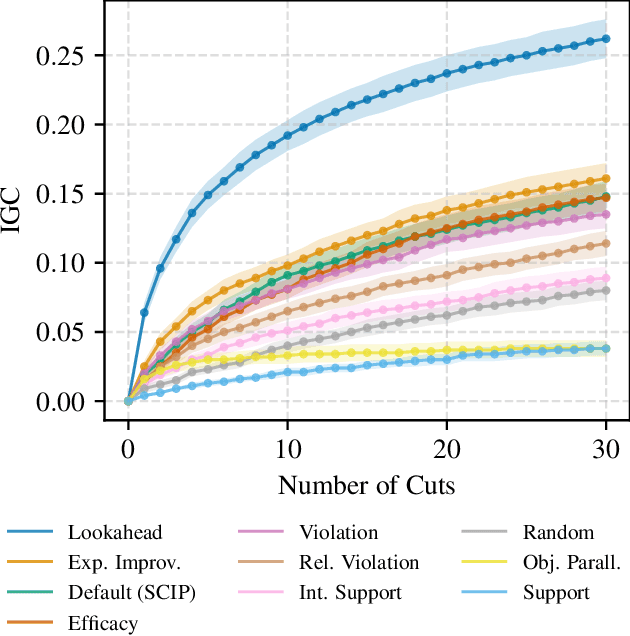

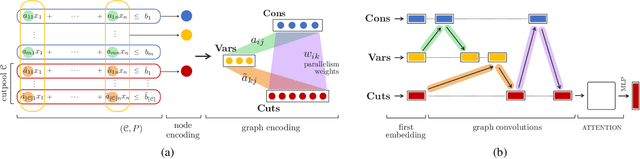
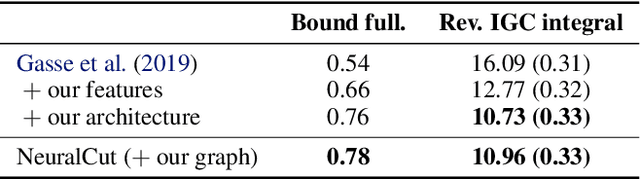
Abstract:Cutting planes are essential for solving mixed-integer linear problems (MILPs), because they facilitate bound improvements on the optimal solution value. For selecting cuts, modern solvers rely on manually designed heuristics that are tuned to gauge the potential effectiveness of cuts. We show that a greedy selection rule explicitly looking ahead to select cuts that yield the best bound improvement delivers strong decisions for cut selection - but is too expensive to be deployed in practice. In response, we propose a new neural architecture (NeuralCut) for imitation learning on the lookahead expert. Our model outperforms standard baselines for cut selection on several synthetic MILP benchmarks. Experiments with a B&C solver for neural network verification further validate our approach, and exhibit the potential of learning methods in this setting.
Augment with Care: Contrastive Learning for the Boolean Satisfiability Problem
Feb 17, 2022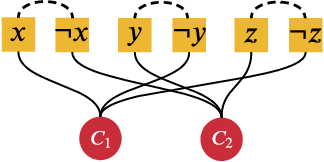
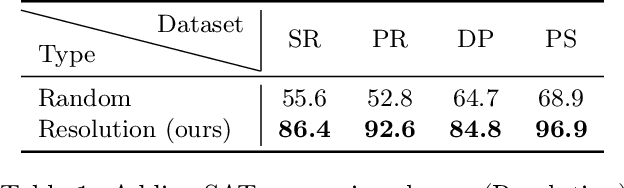
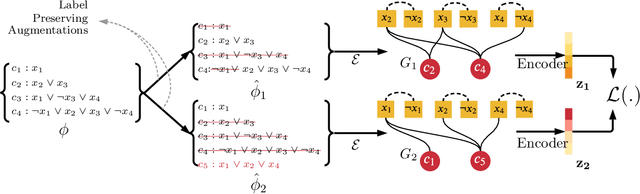
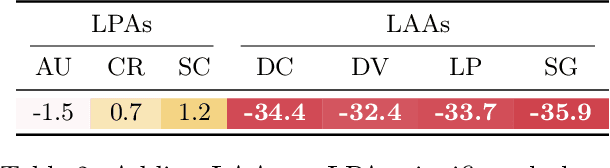
Abstract:Supervised learning can improve the design of state-of-the-art solvers for combinatorial problems, but labelling large numbers of combinatorial instances is often impractical due to exponential worst-case complexity. Inspired by the recent success of contrastive pre-training for images, we conduct a scientific study of the effect of augmentation design on contrastive pre-training for the Boolean satisfiability problem. While typical graph contrastive pre-training uses label-agnostic augmentations, our key insight is that many combinatorial problems have well-studied invariances, which allow for the design of label-preserving augmentations. We find that label-preserving augmentations are critical for the success of contrastive pre-training. We show that our representations are able to achieve comparable test accuracy to fully-supervised learning while using only 1% of the labels. We also demonstrate that our representations are more transferable to larger problems from unseen domains.
Instance-wise algorithm configuration with graph neural networks
Feb 10, 2022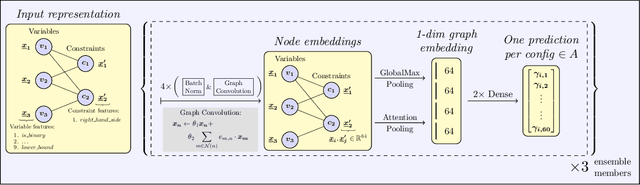

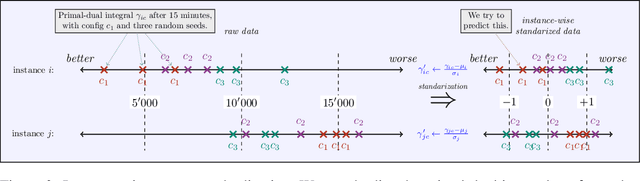
Abstract:We present our submission for the configuration task of the Machine Learning for Combinatorial Optimization (ML4CO) NeurIPS 2021 competition. The configuration task is to predict a good configuration of the open-source solver SCIP to solve a mixed integer linear program (MILP) efficiently. We pose this task as a supervised learning problem: First, we compile a large dataset of the solver performance for various configurations and all provided MILP instances. Second, we use this data to train a graph neural network that learns to predict a good configuration for a specific instance. The submission was tested on the three problem benchmarks of the competition and improved solver performance over the default by 12% and 35% and 8% across the hidden test instances. We ranked 3rd out of 15 on the global leaderboard and won the student leaderboard. We make our code publicly available at \url{https://github.com/RomeoV/ml4co-competition} .
A Review of the Gumbel-max Trick and its Extensions for Discrete Stochasticity in Machine Learning
Oct 04, 2021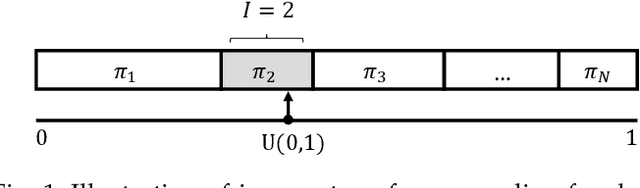
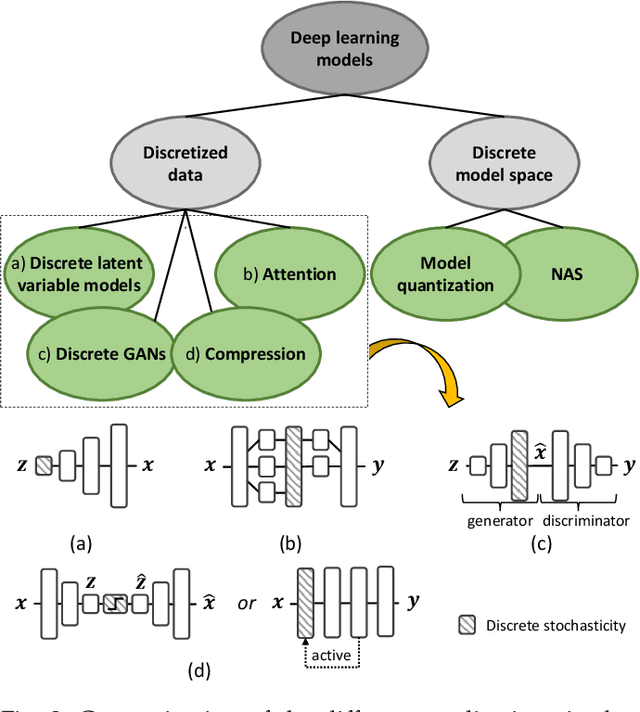
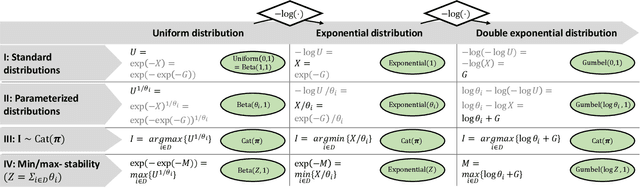
Abstract:The Gumbel-max trick is a method to draw a sample from a categorical distribution, given by its unnormalized (log-)probabilities. Over the past years, the machine learning community has proposed several extensions of this trick to facilitate, e.g., drawing multiple samples, sampling from structured domains, or gradient estimation for error backpropagation in neural network optimization. The goal of this survey article is to present background about the Gumbel-max trick, and to provide a structured overview of its extensions to ease algorithm selection. Moreover, it presents a comprehensive outline of (machine learning) literature in which Gumbel-based algorithms have been leveraged, reviews commonly-made design choices, and sketches a future perspective.
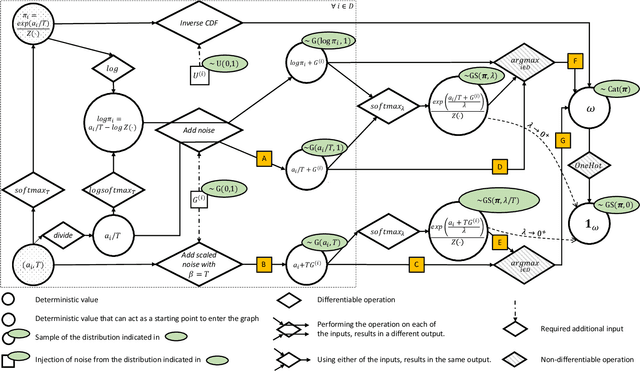
Rao-Blackwellizing the Straight-Through Gumbel-Softmax Gradient Estimator
Oct 09, 2020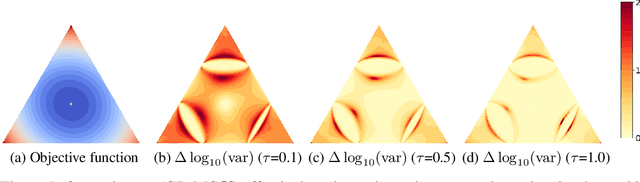

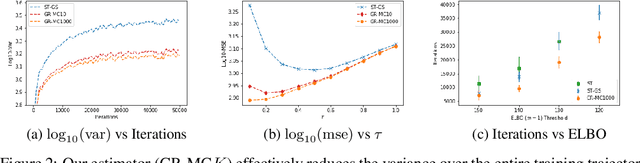
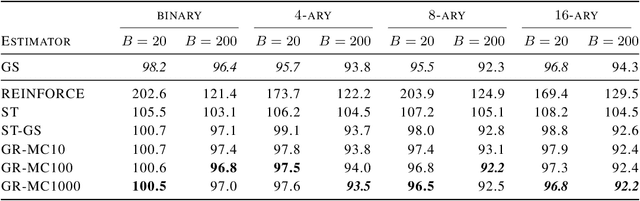
Abstract:Gradient estimation in models with discrete latent variables is a challenging problem, because the simplest unbiased estimators tend to have high variance. To counteract this, modern estimators either introduce bias, rely on multiple function evaluations, or use learned, input-dependent baselines. Thus, there is a need for estimators that require minimal tuning, are computationally cheap, and have low mean squared error. In this paper, we show that the variance of the straight-through variant of the popular Gumbel-Softmax estimator can be reduced through Rao-Blackwellization without increasing the number of function evaluations. This provably reduces the mean squared error. We empirically demonstrate that this leads to variance reduction, faster convergence, and generally improved performance in two unsupervised latent variable models.
Gradient Estimation with Stochastic Softmax Tricks
Jun 15, 2020
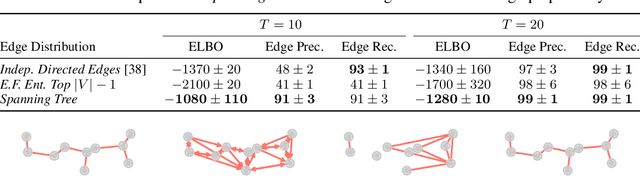
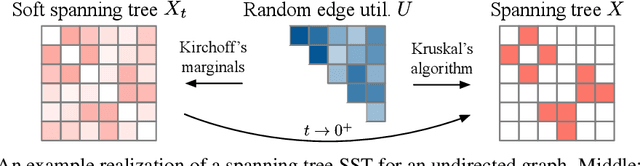
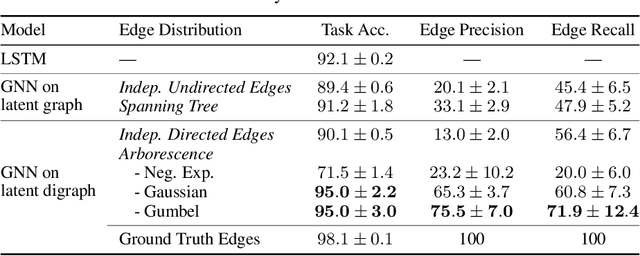
Abstract:The Gumbel-Max trick is the basis of many relaxed gradient estimators. These estimators are easy to implement and low variance, but the goal of scaling them comprehensively to large combinatorial distributions is still outstanding. Working within the perturbation model framework, we introduce stochastic softmax tricks, which generalize the Gumbel-Softmax trick to combinatorial spaces. Our framework is a unified perspective on existing relaxed estimators for perturbation models, and it contains many novel relaxations. We design structured relaxations for subset selection, spanning trees, arborescences, and others. When compared to less structured baselines, we find that stochastic softmax tricks can be used to train latent variable models that perform better and discover more latent structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge