Amortized SHAP values via sparse Fourier function approximation

SHAP values are a popular local feature-attribution method widely used in interpretable and explainable AI. We tackle the problem of efficiently computing these values. We cover both the model-agnostic (black-box) setting, where one only has query access to the model and also the case of (ensembles of) trees where one has access to the structure of the tree. For both the black-box and the tree setting we propose a two-stage approach for estimating SHAP values. Our algorithm's first step harnesses recent results showing that many real-world predictors have a spectral bias that allows us to either exactly represent (in the case of ensembles of decision trees), or efficiently approximate them (in the case of neural networks) using a compact Fourier representation. In the second step of the algorithm, we use the Fourier representation to exactly compute SHAP values. The second step is computationally very cheap because firstly, the representation is compact and secondly, we prove that there exists a closed-form expression for SHAP values for the Fourier basis functions. Furthermore, the expression we derive effectively linearizes the computation into a simple summation and is amenable to parallelization on multiple cores or a GPU. Since the function approximation (first step) is only done once, it allows us to produce Shapley values in an amortized way. We show speedups compared to relevant baseline methods equal levels of accuracy for both the tree and black-box settings. Moreover, this approach introduces a reliable and fine-grained continuous trade-off between computation and accuracy through the sparsity of the Fourier approximation, a feature previously unavailable in all black-box methods.

A Scalable Walsh-Hadamard Regularizer to Overcome the Low-degree Spectral Bias of Neural Networks

Despite the capacity of neural nets to learn arbitrary functions, models trained through gradient descent often exhibit a bias towards ``simpler'' functions. Various notions of simplicity have been introduced to characterize this behavior. Here, we focus on the case of neural networks with discrete (zero-one) inputs through the lens of their Fourier (Walsh-Hadamard) transforms, where the notion of simplicity can be captured through the \emph{degree} of the Fourier coefficients. We empirically show that neural networks have a tendency to learn lower-degree frequencies. We show how this spectral bias towards simpler features can in fact \emph{hurt} the neural network's generalization on real-world datasets. To remedy this we propose a new scalable functional regularization scheme that aids the neural network to learn higher degree frequencies. Our regularizer also helps avoid erroneous identification of low-degree frequencies, which further improves generalization. We extensively evaluate our regularizer on synthetic datasets to gain insights into its behavior. Finally, we show significantly improved generalization on four different datasets compared to standard neural networks and other relevant baselines.

Instance-wise algorithm configuration with graph neural networks

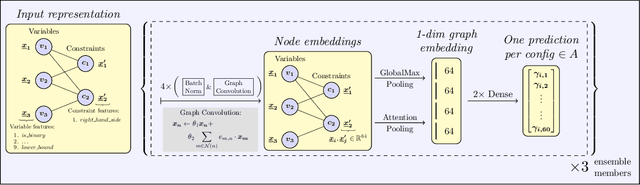
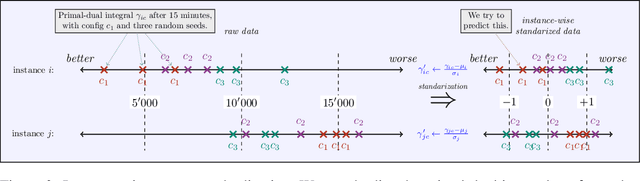
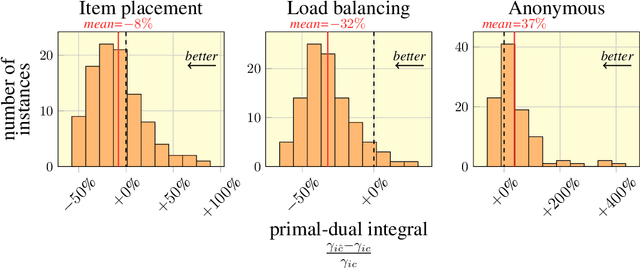
We present our submission for the configuration task of the Machine Learning for Combinatorial Optimization (ML4CO) NeurIPS 2021 competition. The configuration task is to predict a good configuration of the open-source solver SCIP to solve a mixed integer linear program (MILP) efficiently. We pose this task as a supervised learning problem: First, we compile a large dataset of the solver performance for various configurations and all provided MILP instances. Second, we use this data to train a graph neural network that learns to predict a good configuration for a specific instance. The submission was tested on the three problem benchmarks of the competition and improved solver performance over the default by 12% and 35% and 8% across the hidden test instances. We ranked 3rd out of 15 on the global leaderboard and won the student leaderboard. We make our code publicly available at \url{https://github.com/RomeoV/ml4co-competition} .

Learning Set Functions that are Sparse in Non-Orthogonal Fourier Bases

Many applications of machine learning on discrete domains, such as learning preference functions in recommender systems or auctions, can be reduced to estimating a set function that is sparse in the Fourier domain. In this work, we present a new family of algorithms for learning Fourier-sparse set functions. They require at most $nk - k \log_2 k + k$ queries (set function evaluations), under mild conditions on the Fourier coefficients, where $n$ is the size of the ground set and $k$ the number of non-zero Fourier coefficients. In contrast to other work that focused on the orthogonal Walsh-Hadamard transform, our novel algorithms operate with recently introduced non-orthogonal Fourier transforms that offer different notions of Fourier-sparsity. These naturally arise when modeling, e.g., sets of items forming substitutes and complements. We demonstrate effectiveness on several real-world applications.