Learning DAGs and Root Causes from Time-Series Data

We introduce DAG-TFRC, a novel method for learning directed acyclic graphs (DAGs) from time series with few root causes. By this, we mean that the data are generated by a small number of events at certain, unknown nodes and time points under a structural vector autoregression model. For such data, we (i) learn the DAGs representing both the instantaneous and time-lagged dependencies between nodes, and (ii) discover the location and time of the root causes. For synthetic data with few root causes, DAG-TFRC shows superior performance in accuracy and runtime over prior work, scaling up to thousands of nodes. Experiments on simulated and real-world financial data demonstrate the viability of our sparse root cause assumption. On S&P 500 data, DAG-TFRC successfully clusters stocks by sectors and discovers major stock movements as root causes.

The CausalBench challenge: A machine learning contest for gene network inference from single-cell perturbation data

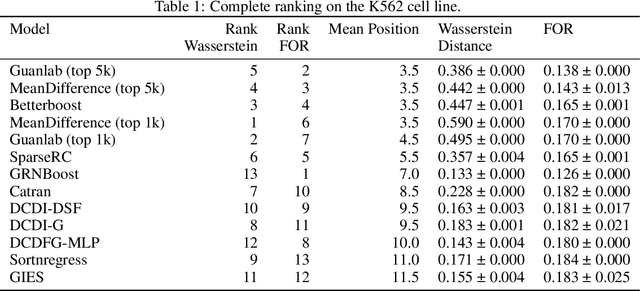
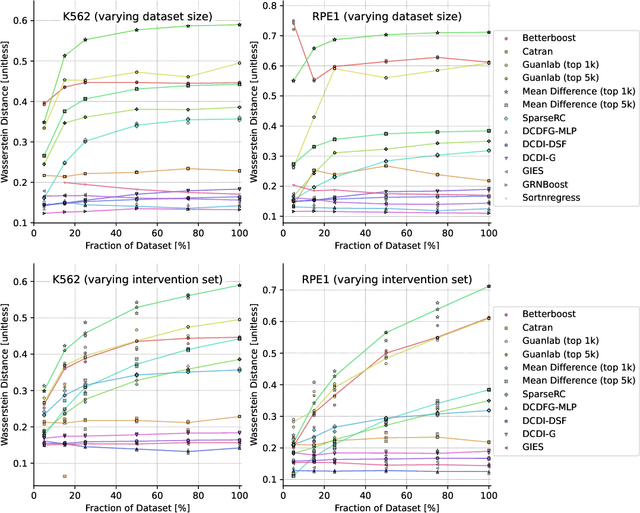
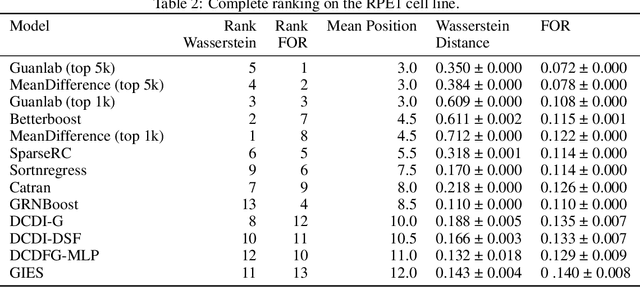
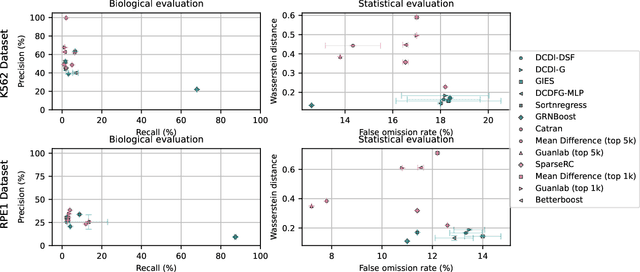
In drug discovery, mapping interactions between genes within cellular systems is a crucial early step. This helps formulate hypotheses regarding molecular mechanisms that could potentially be targeted by future medicines. The CausalBench Challenge was an initiative to invite the machine learning community to advance the state of the art in constructing gene-gene interaction networks. These networks, derived from large-scale, real-world datasets of single cells under various perturbations, are crucial for understanding the causal mechanisms underlying disease biology. Using the framework provided by the CausalBench benchmark, participants were tasked with enhancing the capacity of the state of the art methods to leverage large-scale genetic perturbation data. This report provides an analysis and summary of the methods submitted during the challenge to give a partial image of the state of the art at the time of the challenge. The winning solutions significantly improved performance compared to previous baselines, establishing a new state of the art for this critical task in biology and medicine.

QIGen: Generating Efficient Kernels for Quantized Inference on Large Language Models

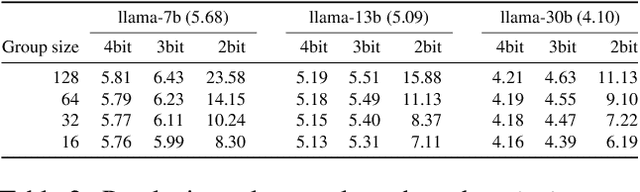
We present ongoing work on a new automatic code generation approach for supporting quantized generative inference on LLMs such as LLaMA or OPT on off-the-shelf CPUs. Our approach is informed by the target architecture and a performance model, including both hardware characteristics and method-specific accuracy constraints. Results on CPU-based inference for LLaMA models show that our approach can lead to high performance and high accuracy, comparing favorably to the best existing open-source solution. A preliminary implementation is available at https://github.com/IST-DASLab/QIGen.

Learning DAGs from Data with Few Root Causes

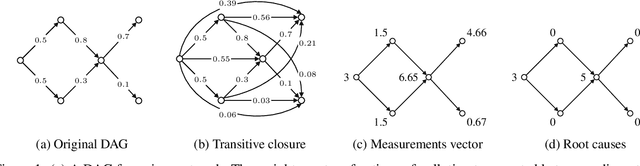
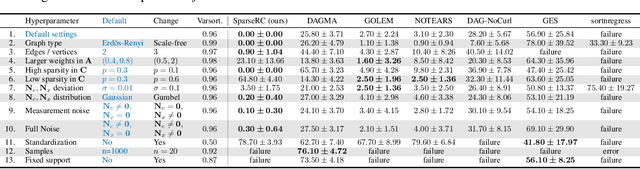
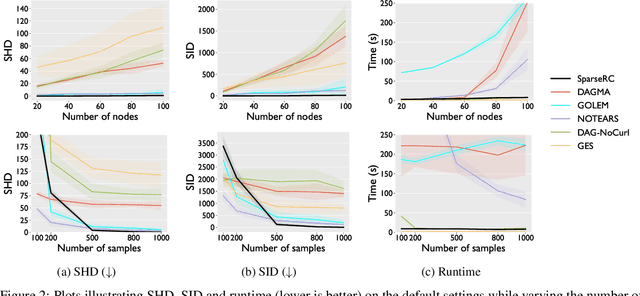
We present a novel perspective and algorithm for learning directed acyclic graphs (DAGs) from data generated by a linear structural equation model (SEM). First, we show that a linear SEM can be viewed as a linear transform that, in prior work, computes the data from a dense input vector of random valued root causes (as we will call them) associated with the nodes. Instead, we consider the case of (approximately) few root causes and also introduce noise in the measurement of the data. Intuitively, this means that the DAG data is produced by few data-generating events whose effect percolates through the DAG. We prove identifiability in this new setting and show that the true DAG is the global minimizer of the $L^0$-norm of the vector of root causes. For data with few root causes, with and without noise, we show superior performance compared to prior DAG learning methods.

Causal Fourier Analysis on Directed Acyclic Graphs and Posets

We present a novel form of Fourier analysis, and associated signal processing concepts, for signals (or data) indexed by edge-weighted directed acyclic graphs (DAGs). This means that our Fourier basis yields an eigendecomposition of a suitable notion of shift and convolution operators that we define. DAGs are the common model to capture causal relationships between data and our framework is causal in that shift, convolution, and Fourier transform are computed only from predecessors in the DAG. The Fourier transform requires the transitive closure of the DAG for which several forms are possible depending on the interpretation of the edge weights. Examples include level of influence, distance, or pollution distribution. Our framework is different from prior GSP: it is specific to DAGs and leverages, and extends, the classical theory of Moebius inversion from combinatorics. For a prototypical application we consider DAGs modeling dynamic networks in which edges change over time. Specifically, we model the spread of an infection on such a DAG obtained from real-world contact tracing data and learn the infection signal from samples assuming sparsity in the Fourier domain.

Precise Multi-Neuron Abstractions for Neural Network Certification

Formal verification of neural networks is critical for their safe adoption in real-world applications. However, designing a verifier which can handle realistic networks in a precise manner remains an open and difficult challenge. In this paper, we take a major step in addressing this challenge and present a new framework, called PRIMA, that computes precise convex approximations of arbitrary non-linear activations. PRIMA is based on novel approximation algorithms that compute the convex hull of polytopes, leveraging concepts from computational geometry. The algorithms have polynomial complexity, yield fewer constraints, and minimize precision loss. We evaluate the effectiveness of PRIMA on challenging neural networks with ReLU, Sigmoid, and Tanh activations. Our results show that PRIMA is significantly more precise than the state-of-the-art, verifying robustness for up to 16%, 30%, and 34% more images than prior work on ReLU-, Sigmoid-, and Tanh-based networks, respectively.

Learning Set Functions that are Sparse in Non-Orthogonal Fourier Bases

Many applications of machine learning on discrete domains, such as learning preference functions in recommender systems or auctions, can be reduced to estimating a set function that is sparse in the Fourier domain. In this work, we present a new family of algorithms for learning Fourier-sparse set functions. They require at most $nk - k \log_2 k + k$ queries (set function evaluations), under mild conditions on the Fourier coefficients, where $n$ is the size of the ground set and $k$ the number of non-zero Fourier coefficients. In contrast to other work that focused on the orthogonal Walsh-Hadamard transform, our novel algorithms operate with recently introduced non-orthogonal Fourier transforms that offer different notions of Fourier-sparsity. These naturally arise when modeling, e.g., sets of items forming substitutes and complements. We demonstrate effectiveness on several real-world applications.

Neural Network Robustness Verification on GPUs

Certifying the robustness of neural networks against adversarial attacks is critical to their reliable adoption in real-world systems including autonomous driving and medical diagnosis. Unfortunately, state-of-the-art verifiers either do not scale to larger networks or are too imprecise to prove robustness, which limits their practical adoption. In this work, we introduce GPUPoly, a scalable verifier that can prove the robustness of significantly larger deep neural networks than possible with prior work. The key insight behind GPUPoly is the design of custom, sound polyhedra algorithms for neural network verification on a GPU. Our algorithms leverage the available GPU parallelism and the inherent sparsity of the underlying neural network verification task. GPUPoly scales to very large networks: for example, it can prove the robustness of a 1M neuron, 34-layer deep residual network in about 1 minute. We believe GPUPoly is a promising step towards the practical verification of large real-world networks.

Discrete Signal Processing with Set Functions

Set functions are functions (or signals) indexed by the power set (set of all subsets) of a finite set $N$. They are ubiquitous in many application domains. For example, they are equivalent to node- or edge-weighted hypergraphs and to cooperative games in game theory. Further, the subclass of submodular functions occurs in many optimization and machine learning problems. In this paper, we derive discrete-set signal processing (SP), a shift-invariant linear signal processing framework for set functions. Discrete-set SP provides suitable definitions of shift, shift-invariant systems, convolution, Fourier transform, frequency response, and other SP concepts. Different variants are possible due to different possible shifts. Discrete-set SP is inherently different from graph SP as it distinguishes the neighbors of an index $A\subseteq N$, i.e., those with one elements more or less by providing $n = |N|$ shifts. Finally, we show three prototypical applications and experiments with discrete-set SP including compression in submodular function optimization, sampling for preference elicitation in auctions, and novel power set neural networks.

Powerset Convolutional Neural Networks

We present a novel class of convolutional neural networks (CNNs) for set functions, i.e., data indexed with the powerset of a finite set. The convolutions are derived as linear, shift-equivariant functions for various notions of shifts on set functions. The framework is fundamentally different from graph convolutions based on the Laplacian, as it provides not one but several basic shifts, one for each element in the ground set. Prototypical experiments with several set function classification tasks on synthetic datasets and on datasets derived from real-world hypergraphs demonstrate the potential of our new powerset CNNs.