Learning DAGs and Root Causes from Time-Series Data

We introduce DAG-TFRC, a novel method for learning directed acyclic graphs (DAGs) from time series with few root causes. By this, we mean that the data are generated by a small number of events at certain, unknown nodes and time points under a structural vector autoregression model. For such data, we (i) learn the DAGs representing both the instantaneous and time-lagged dependencies between nodes, and (ii) discover the location and time of the root causes. For synthetic data with few root causes, DAG-TFRC shows superior performance in accuracy and runtime over prior work, scaling up to thousands of nodes. Experiments on simulated and real-world financial data demonstrate the viability of our sparse root cause assumption. On S&P 500 data, DAG-TFRC successfully clusters stocks by sectors and discovers major stock movements as root causes.

TropNNC: Structured Neural Network Compression Using Tropical Geometry

We present TropNNC, a structured pruning framework for compressing neural networks with linear and convolutional layers and ReLU activations. Our approximation is based on a geometrical approach to machine/deep learning, using tropical geometry and extending the work of Misiakos et al. (2022). We use the Hausdorff distance of zonotopes in its standard continuous form to achieve a tighter approximation bound for tropical polynomials compared to Misiakos et al. (2022). This enhancement allows for superior functional approximations of neural networks, leading to a more effective compression algorithm. Our method is significantly easier to implement compared to other frameworks, and does not depend on the availability of training data samples. We validate our framework through extensive empirical evaluations on the MNIST, CIFAR, and ImageNet datasets. Our results demonstrate that TropNNC achieves performance on par with the state-of-the-art method ThiNet, even surpassing it in compressing linear layers, and to the best of our knowledge, it is the first method that achieves this using tropical geometry.

The CausalBench challenge: A machine learning contest for gene network inference from single-cell perturbation data

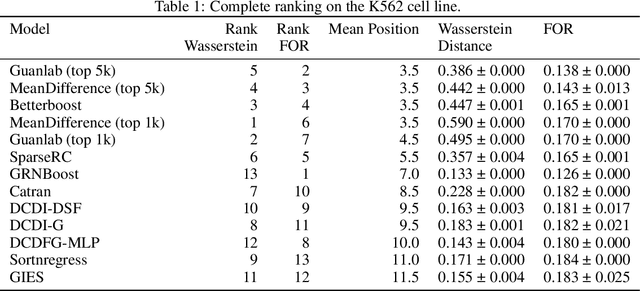
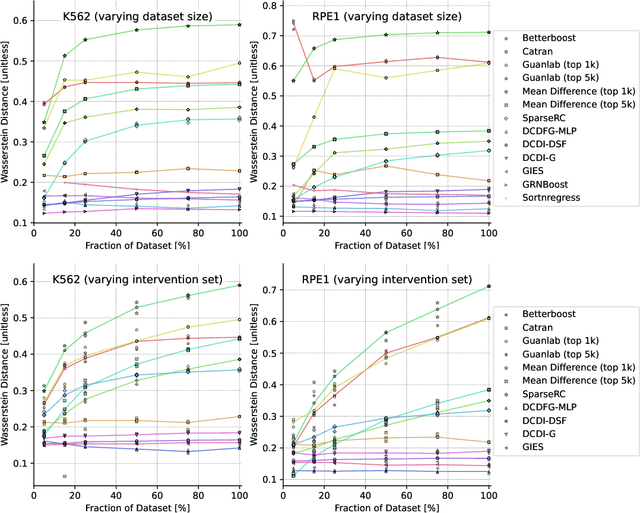
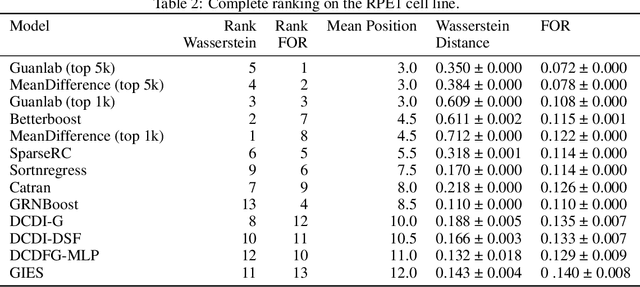
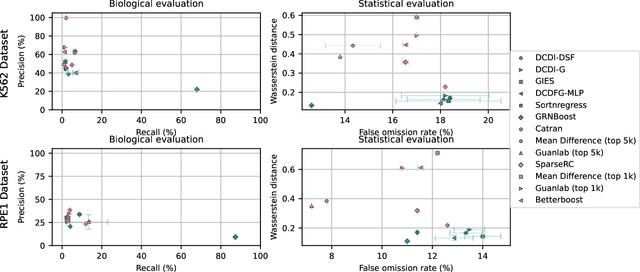
In drug discovery, mapping interactions between genes within cellular systems is a crucial early step. This helps formulate hypotheses regarding molecular mechanisms that could potentially be targeted by future medicines. The CausalBench Challenge was an initiative to invite the machine learning community to advance the state of the art in constructing gene-gene interaction networks. These networks, derived from large-scale, real-world datasets of single cells under various perturbations, are crucial for understanding the causal mechanisms underlying disease biology. Using the framework provided by the CausalBench benchmark, participants were tasked with enhancing the capacity of the state of the art methods to leverage large-scale genetic perturbation data. This report provides an analysis and summary of the methods submitted during the challenge to give a partial image of the state of the art at the time of the challenge. The winning solutions significantly improved performance compared to previous baselines, establishing a new state of the art for this critical task in biology and medicine.

Learning DAGs from Data with Few Root Causes

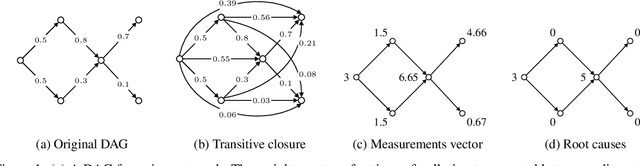
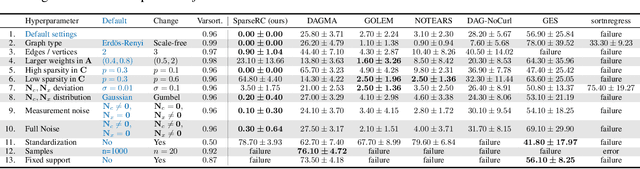
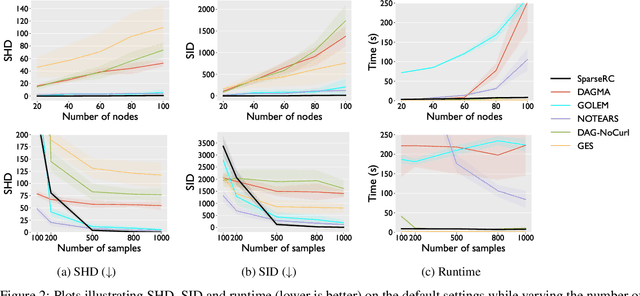
We present a novel perspective and algorithm for learning directed acyclic graphs (DAGs) from data generated by a linear structural equation model (SEM). First, we show that a linear SEM can be viewed as a linear transform that, in prior work, computes the data from a dense input vector of random valued root causes (as we will call them) associated with the nodes. Instead, we consider the case of (approximately) few root causes and also introduce noise in the measurement of the data. Intuitively, this means that the DAG data is produced by few data-generating events whose effect percolates through the DAG. We prove identifiability in this new setting and show that the true DAG is the global minimizer of the $L^0$-norm of the vector of root causes. For data with few root causes, with and without noise, we show superior performance compared to prior DAG learning methods.