Causal Fourier Analysis on Directed Acyclic Graphs and Posets

We present a novel form of Fourier analysis, and associated signal processing concepts, for signals (or data) indexed by edge-weighted directed acyclic graphs (DAGs). This means that our Fourier basis yields an eigendecomposition of a suitable notion of shift and convolution operators that we define. DAGs are the common model to capture causal relationships between data and our framework is causal in that shift, convolution, and Fourier transform are computed only from predecessors in the DAG. The Fourier transform requires the transitive closure of the DAG for which several forms are possible depending on the interpretation of the edge weights. Examples include level of influence, distance, or pollution distribution. Our framework is different from prior GSP: it is specific to DAGs and leverages, and extends, the classical theory of Moebius inversion from combinatorics. For a prototypical application we consider DAGs modeling dynamic networks in which edges change over time. Specifically, we model the spread of an infection on such a DAG obtained from real-world contact tracing data and learn the infection signal from samples assuming sparsity in the Fourier domain.

Learning Set Functions that are Sparse in Non-Orthogonal Fourier Bases

Many applications of machine learning on discrete domains, such as learning preference functions in recommender systems or auctions, can be reduced to estimating a set function that is sparse in the Fourier domain. In this work, we present a new family of algorithms for learning Fourier-sparse set functions. They require at most $nk - k \log_2 k + k$ queries (set function evaluations), under mild conditions on the Fourier coefficients, where $n$ is the size of the ground set and $k$ the number of non-zero Fourier coefficients. In contrast to other work that focused on the orthogonal Walsh-Hadamard transform, our novel algorithms operate with recently introduced non-orthogonal Fourier transforms that offer different notions of Fourier-sparsity. These naturally arise when modeling, e.g., sets of items forming substitutes and complements. We demonstrate effectiveness on several real-world applications.

Dynamical Component Analysis (DyCA) and its application on epileptic EEG

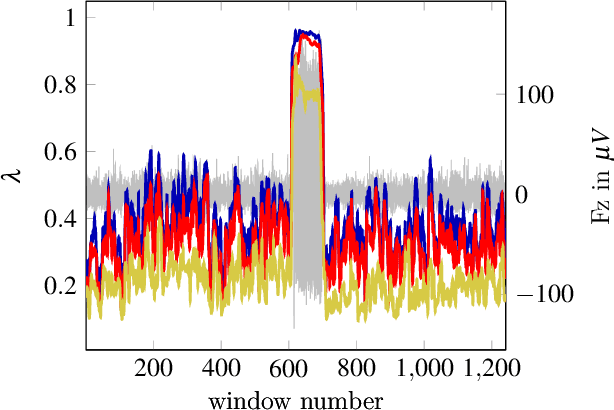
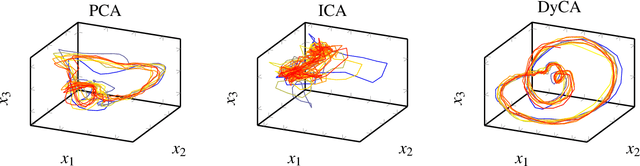
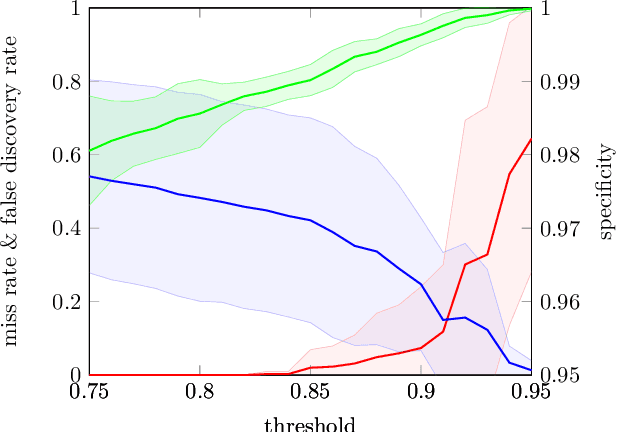
Dynamical Component Analysis (DyCA) is a recently-proposed method to detect projection vectors to reduce the dimensionality of multi-variate deterministic datasets. It is based on the solution of a generalized eigenvalue problem and therefore straight forward to implement. DyCA is introduced and applied to EEG data of epileptic seizures. The obtained eigenvectors are used to project the signal and the corresponding trajectories in phase space are compared with PCA and ICA-projections. The eigenvalues of DyCA are utilized for seizure detection and the obtained results in terms of specificity, false discovery rate and miss rate are compared to other seizure detection algorithms.

Dynamical Component Analysis (DyCA): Dimensionality Reduction For High-Dimensional Deterministic Time-Series

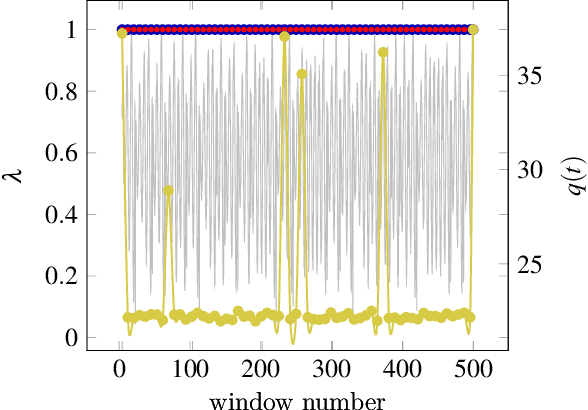
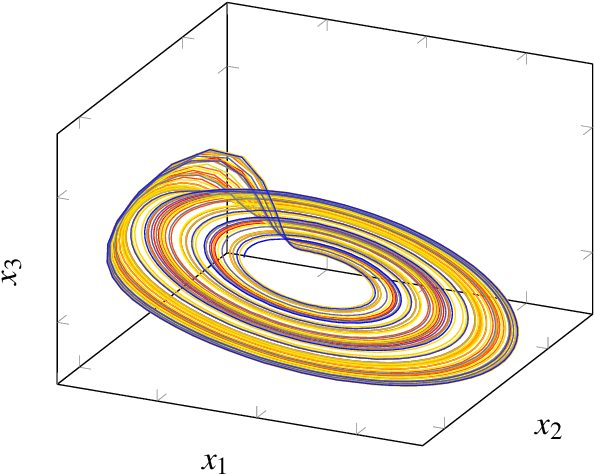
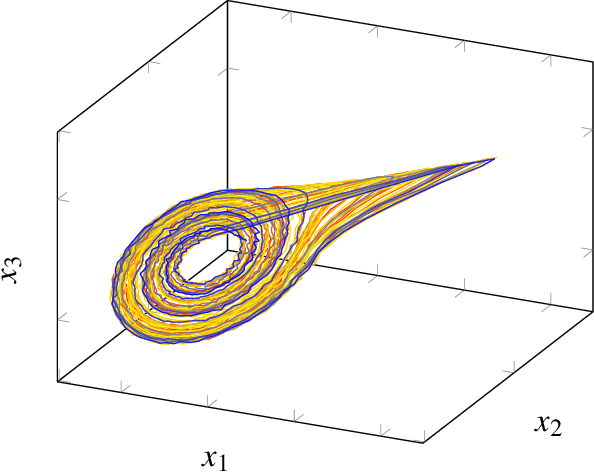
Multivariate signal processing is often based on dimensionality reduction techniques. We propose a new method, Dynamical Component Analysis (DyCA), leading to a classification of the underlying dynamics and - for a certain type of dynamics - to a signal subspace representing the dynamics of the data. In this paper the algorithm is derived leading to a generalized eigenvalue problem of correlation matrices. The application of the DyCA on high-dimensional chaotic signals is presented both for simulated data as well as real EEG data of epileptic seizures.