Dynamical Component Analysis (DyCA): Dimensionality Reduction For High-Dimensional Deterministic Time-Series
Paper and Code
Jul 26, 2018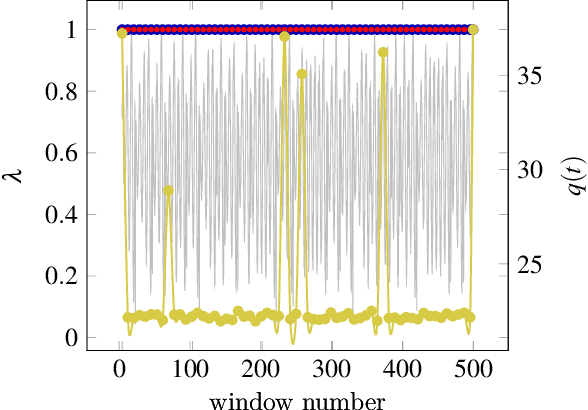
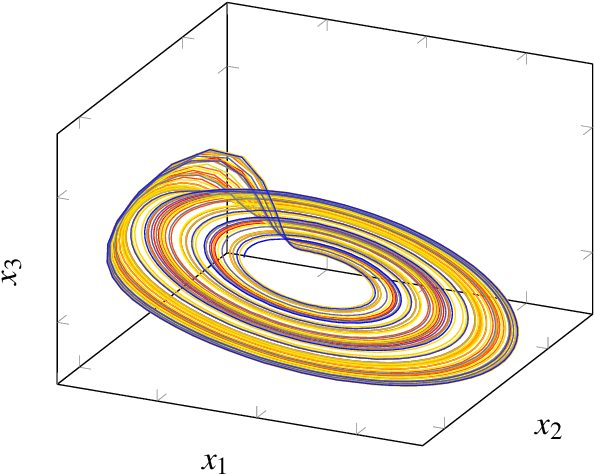

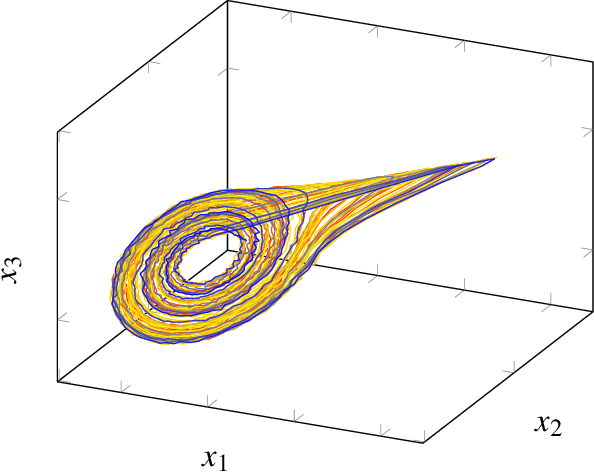
Multivariate signal processing is often based on dimensionality reduction techniques. We propose a new method, Dynamical Component Analysis (DyCA), leading to a classification of the underlying dynamics and - for a certain type of dynamics - to a signal subspace representing the dynamics of the data. In this paper the algorithm is derived leading to a generalized eigenvalue problem of correlation matrices. The application of the DyCA on high-dimensional chaotic signals is presented both for simulated data as well as real EEG data of epileptic seizures.
* Accepted for 2018 IEEE INTERNATIONAL WORKSHOP ON MACHINE LEARNING FOR
SIGNAL PROCESSING; 7 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge