Dynamical Component Analysis (DyCA) and its application on epileptic EEG

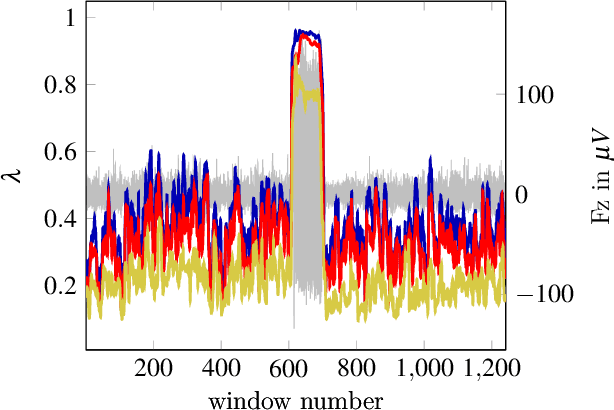
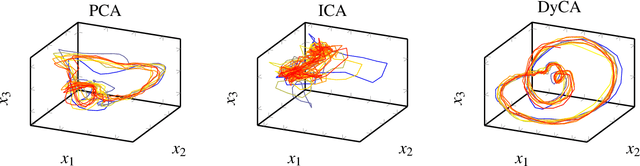
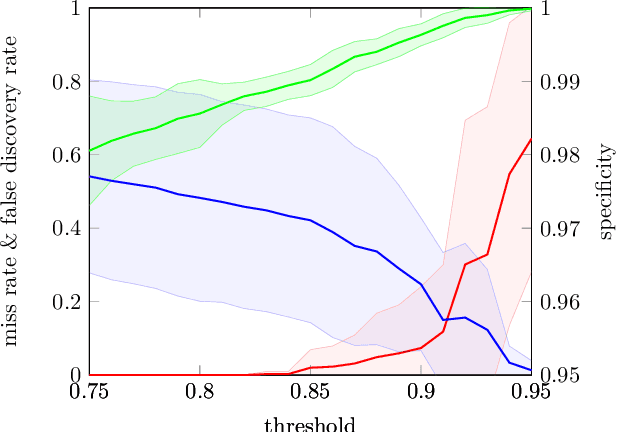
Dynamical Component Analysis (DyCA) is a recently-proposed method to detect projection vectors to reduce the dimensionality of multi-variate deterministic datasets. It is based on the solution of a generalized eigenvalue problem and therefore straight forward to implement. DyCA is introduced and applied to EEG data of epileptic seizures. The obtained eigenvectors are used to project the signal and the corresponding trajectories in phase space are compared with PCA and ICA-projections. The eigenvalues of DyCA are utilized for seizure detection and the obtained results in terms of specificity, false discovery rate and miss rate are compared to other seizure detection algorithms.

Dynamical Component Analysis (DyCA): Dimensionality Reduction For High-Dimensional Deterministic Time-Series

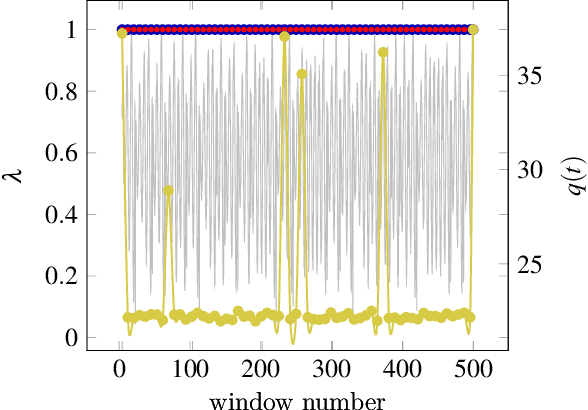
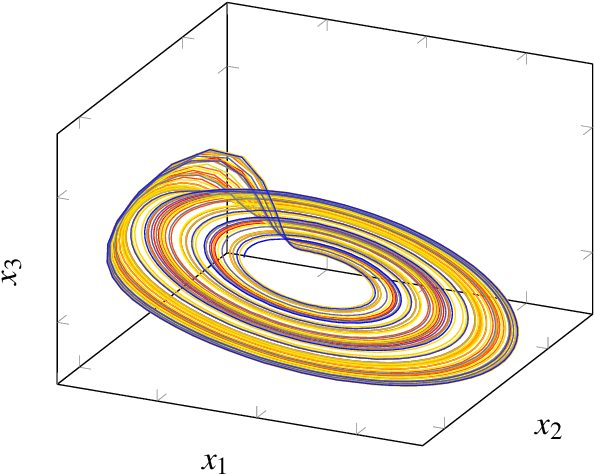
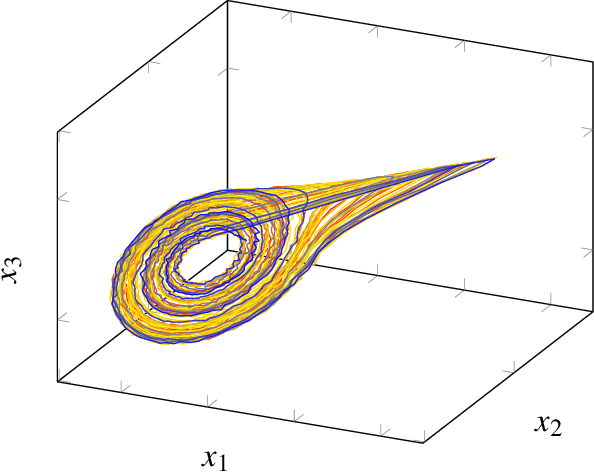
Multivariate signal processing is often based on dimensionality reduction techniques. We propose a new method, Dynamical Component Analysis (DyCA), leading to a classification of the underlying dynamics and - for a certain type of dynamics - to a signal subspace representing the dynamics of the data. In this paper the algorithm is derived leading to a generalized eigenvalue problem of correlation matrices. The application of the DyCA on high-dimensional chaotic signals is presented both for simulated data as well as real EEG data of epileptic seizures.