FlowFixer: Towards Detail-Preserving Subject-Driven Generation

We present FlowFixer, a refinement framework for subject-driven generation (SDG) that restores fine details lost during generation caused by changes in scale and perspective of a subject. FlowFixer proposes direct image-to-image translation from visual references, avoiding ambiguities in language prompts. To enable image-to-image training, we introduce a one-step denoising scheme to generate self-supervised training data, which automatically removes high-frequency details while preserving global structure, effectively simulating real-world SDG errors. We further propose a keypoint matching-based metric to properly assess fidelity in details beyond semantic similarities usually measured by CLIP or DINO. Experimental results demonstrate that FlowFixer outperforms state-of-the-art SDG methods in both qualitative and quantitative evaluations, setting a new benchmark for high-fidelity subject-driven generation.

Learning-Guided Rolling Horizon Optimization for Long-Horizon Flexible Job-Shop Scheduling

Long-horizon combinatorial optimization problems (COPs), such as the Flexible Job-Shop Scheduling Problem (FJSP), often involve complex, interdependent decisions over extended time frames, posing significant challenges for existing solvers. While Rolling Horizon Optimization (RHO) addresses this by decomposing problems into overlapping shorter-horizon subproblems, such overlap often involves redundant computations. In this paper, we present L-RHO, the first learning-guided RHO framework for COPs. L-RHO employs a neural network to intelligently fix variables that in hindsight did not need to be re-optimized, resulting in smaller and thus easier-to-solve subproblems. For FJSP, this means identifying operations with unchanged machine assignments between consecutive subproblems. Applied to FJSP, L-RHO accelerates RHO by up to 54% while significantly improving solution quality, outperforming other heuristic and learning-based baselines. We also provide in-depth discussions and verify the desirable adaptability and generalization of L-RHO across numerous FJSP variates, distributions, online scenarios and benchmark instances. Moreover, we provide a theoretical analysis to elucidate the conditions under which learning is beneficial.

TLMCM Network for Medical Image Hierarchical Multi-Label Classification

Medical Image Hierarchical Multi-Label Classification (MI-HMC) is of paramount importance in modern healthcare, presenting two significant challenges: data imbalance and \textit{hierarchy constraint}. Existing solutions involve complex model architecture design or domain-specific preprocessing, demanding considerable expertise or effort in implementation. To address these limitations, this paper proposes Transfer Learning with Maximum Constraint Module (TLMCM) network for the MI-HMC task. The TLMCM network offers a novel approach to overcome the aforementioned challenges, outperforming existing methods based on the Area Under the Average Precision and Recall Curve($AU\overline{(PRC)}$) metric. In addition, this research proposes two novel accuracy metrics, $EMR$ and $HammingAccuracy$, which have not been extensively explored in the context of the MI-HMC task. Experimental results demonstrate that the TLMCM network achieves high multi-label prediction accuracy($80\%$-$90\%$) for MI-HMC tasks, making it a valuable contribution to healthcare domain applications.

Learning to Configure Separators in Branch-and-Cut

Cutting planes are crucial in solving mixed integer linear programs (MILP) as they facilitate bound improvements on the optimal solution. Modern MILP solvers rely on a variety of separators to generate a diverse set of cutting planes by invoking the separators frequently during the solving process. This work identifies that MILP solvers can be drastically accelerated by appropriately selecting separators to activate. As the combinatorial separator selection space imposes challenges for machine learning, we learn to separate by proposing a novel data-driven strategy to restrict the selection space and a learning-guided algorithm on the restricted space. Our method predicts instance-aware separator configurations which can dynamically adapt during the solve, effectively accelerating the open source MILP solver SCIP by improving the relative solve time up to 72% and 37% on synthetic and real-world MILP benchmarks. Our work complements recent work on learning to select cutting planes and highlights the importance of separator management.

Generalization in Deep RL for TSP Problems via Equivariance and Local Search

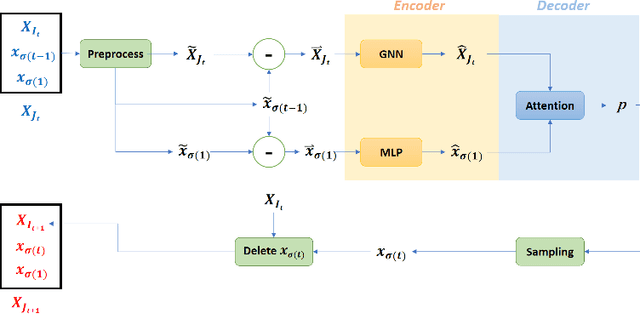
Deep reinforcement learning (RL) has proved to be a competitive heuristic for solving small-sized instances of traveling salesman problems (TSP), but its performance on larger-sized instances is insufficient. Since training on large instances is impractical, we design a novel deep RL approach with a focus on generalizability. Our proposition consisting of a simple deep learning architecture that learns with novel RL training techniques, exploits two main ideas. First, we exploit equivariance to facilitate training. Second, we interleave efficient local search heuristics with the usual RL training to smooth the value landscape. In order to validate the whole approach, we empirically evaluate our proposition on random and realistic TSP problems against relevant state-of-the-art deep RL methods. Moreover, we present an ablation study to understand the contribution of each of its component

Improving Generalization of Deep Reinforcement Learning-based TSP Solvers

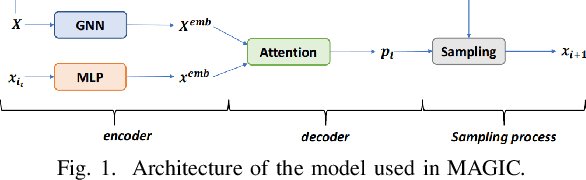
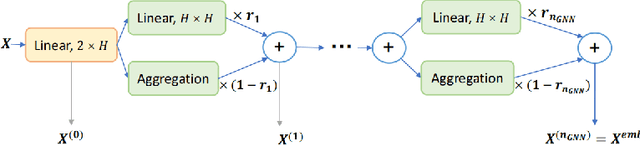
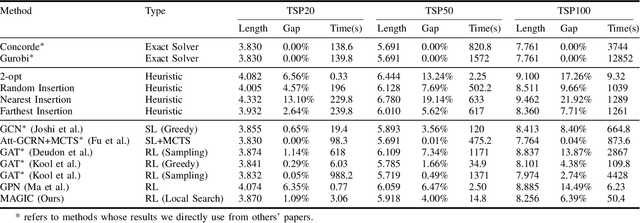
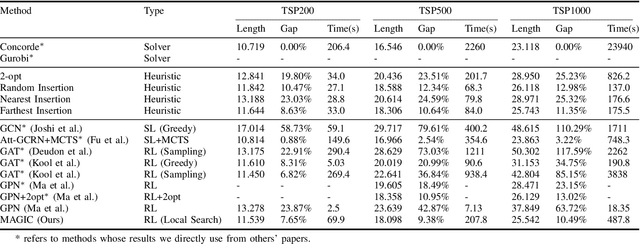
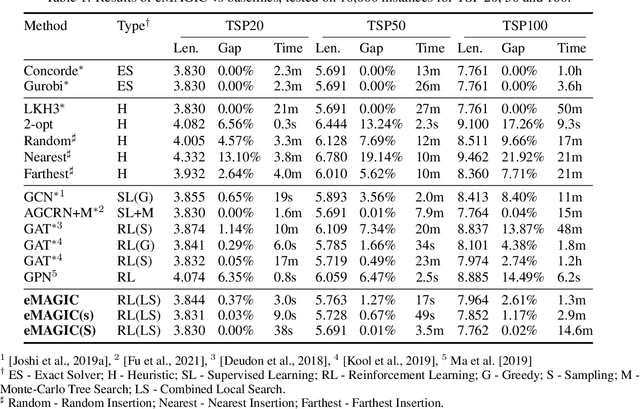
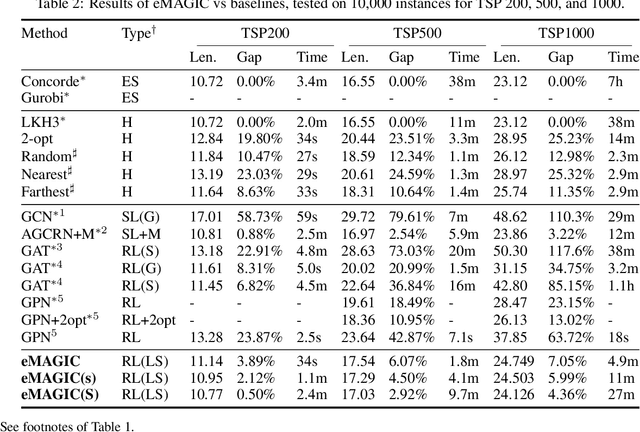
Recent work applying deep reinforcement learning (DRL) to solve traveling salesman problems (TSP) has shown that DRL-based solvers can be fast and competitive with TSP heuristics for small instances, but do not generalize well to larger instances. In this work, we propose a novel approach named MAGIC that includes a deep learning architecture and a DRL training method. Our architecture, which integrates a multilayer perceptron, a graph neural network, and an attention model, defines a stochastic policy that sequentially generates a TSP solution. Our training method includes several innovations: (1) we interleave DRL policy gradient updates with local search (using a new local search technique), (2) we use a novel simple baseline, and (3) we apply curriculum learning. Finally, we empirically demonstrate that MAGIC is superior to other DRL-based methods on random TSP instances, both in terms of performance and generalizability. Moreover, our method compares favorably against TSP heuristics and other state-of-the-art approach in terms of performance and computational time.