Learning To Cut By Looking Ahead: Cutting Plane Selection via Imitation Learning

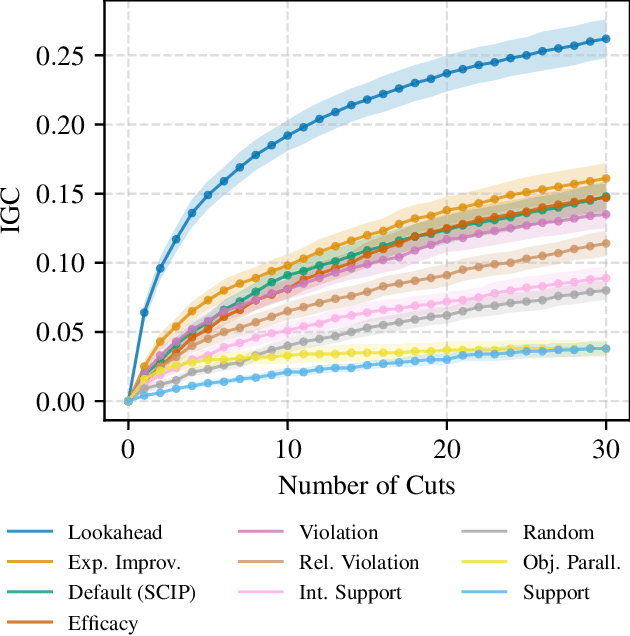
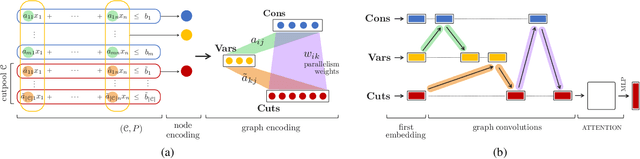
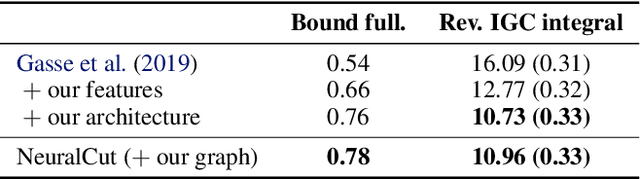
Cutting planes are essential for solving mixed-integer linear problems (MILPs), because they facilitate bound improvements on the optimal solution value. For selecting cuts, modern solvers rely on manually designed heuristics that are tuned to gauge the potential effectiveness of cuts. We show that a greedy selection rule explicitly looking ahead to select cuts that yield the best bound improvement delivers strong decisions for cut selection - but is too expensive to be deployed in practice. In response, we propose a new neural architecture (NeuralCut) for imitation learning on the lookahead expert. Our model outperforms standard baselines for cut selection on several synthetic MILP benchmarks. Experiments with a B&C solver for neural network verification further validate our approach, and exhibit the potential of learning methods in this setting.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

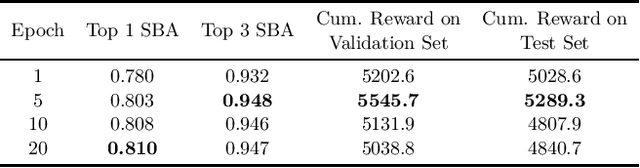
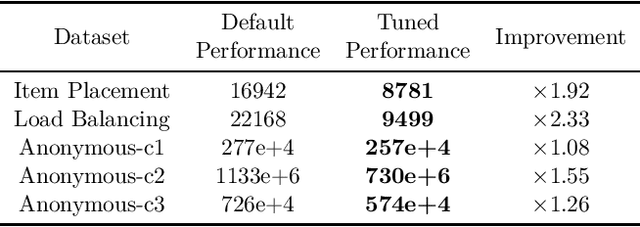
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.

Parameterizing Branch-and-Bound Search Trees to Learn Branching Policies

Branch and Bound (B&B) is the exact tree search method typically used to solve Mixed-Integer Linear Programming problems (MILPs). Learning branching policies for MILP has become an active research area, with most works proposing to imitate the strong branching rule and specialize it to distinct classes of problems. We aim instead at learning a policy that generalizes across heterogeneous MILPs: our main hypothesis is that parameterizing the state of the B&B search tree can significantly aid this type of generalization. We propose a novel imitation learning framework, and introduce new input features and architectures to represent branching. Experiments on MILP benchmark instances clearly show the advantages of incorporating to a baseline model an explicit parameterization of the state of the search tree to modulate the branching decisions. The resulting policy reaches higher accuracy than the baseline, and on average explores smaller B&B trees, while effectively allowing generalization to generic unseen instances.