Exploring the Power of Graph Neural Networks in Solving Linear Optimization Problems

Recently, machine learning, particularly message-passing graph neural networks (MPNNs), has gained traction in enhancing exact optimization algorithms. For example, MPNNs speed up solving mixed-integer optimization problems by imitating computational intensive heuristics like strong branching, which entails solving multiple linear optimization problems (LPs). Despite the empirical success, the reasons behind MPNNs' effectiveness in emulating linear optimization remain largely unclear. Here, we show that MPNNs can simulate standard interior-point methods for LPs, explaining their practical success. Furthermore, we highlight how MPNNs can serve as a lightweight proxy for solving LPs, adapting to a given problem instance distribution. Empirically, we show that MPNNs solve LP relaxations of standard combinatorial optimization problems close to optimality, often surpassing conventional solvers and competing approaches in solving time.

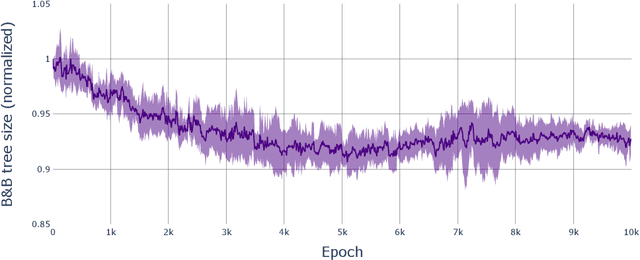
Learning to Compare Nodes in Branch and Bound with Graph Neural Networks

Branch-and-bound approaches in integer programming require ordering portions of the space to explore next, a problem known as node comparison. We propose a new siamese graph neural network model to tackle this problem, where the nodes are represented as bipartite graphs with attributes. Similar to prior work, we train our model to imitate a diving oracle that plunges towards the optimal solution. We evaluate our method by solving the instances in a plain framework where the nodes are explored according to their rank. On three NP-hard benchmarks chosen to be particularly primal-difficult, our approach leads to faster solving and smaller branch- and-bound trees than the default ranking function of the open-source solver SCIP, as well as competing machine learning methods. Moreover, these results generalize to instances larger than used for training. Code for reproducing the experiments can be found at https://github.com/ds4dm/learn2comparenodes.

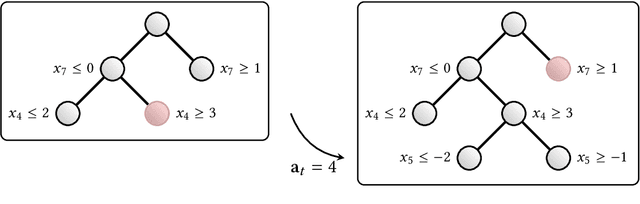
Learning to branch with Tree MDPs

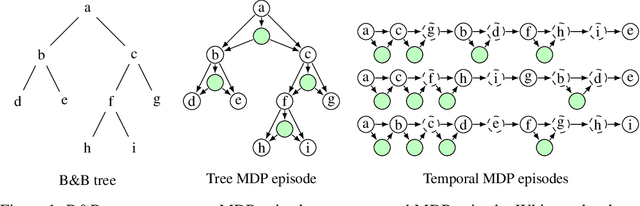
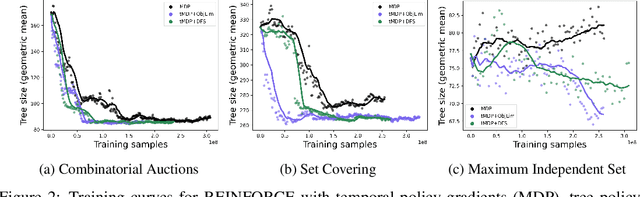
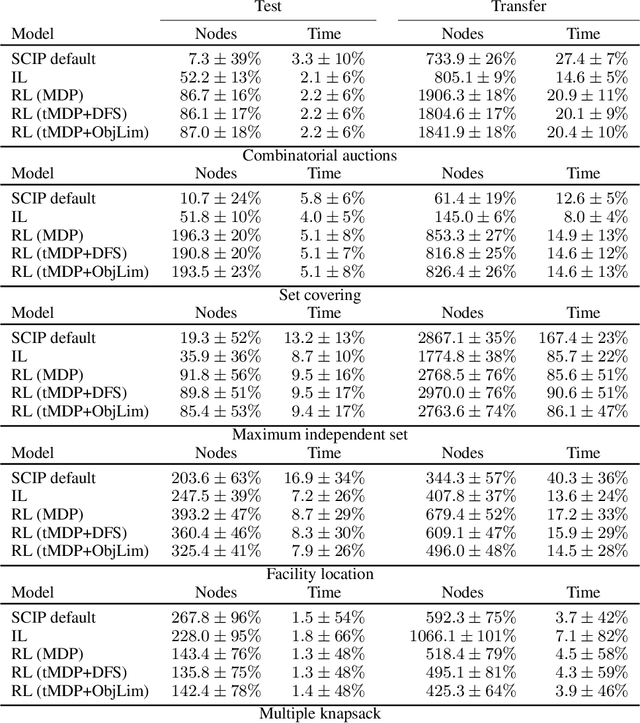
State-of-the-art Mixed Integer Linear Program (MILP) solvers combine systematic tree search with a plethora of hard-coded heuristics, such as the branching rule. The idea of learning branching rules from data has received increasing attention recently, and promising results have been obtained by learning fast approximations of the strong branching expert. In this work, we instead propose to learn branching rules from scratch via Reinforcement Learning (RL). We revisit the work of Etheve et al. (2020) and propose tree Markov Decision Processes, or tree MDPs, a generalization of temporal MDPs that provides a more suitable framework for learning to branch. We derive a tree policy gradient theorem, which exhibits a better credit assignment compared to its temporal counterpart. We demonstrate through computational experiments that tree MDPs improve the learning convergence, and offer a promising framework for tackling the learning-to-branch problem in MILPs.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

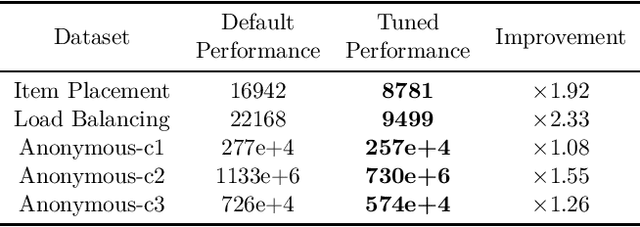
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.

Ecole: A Library for Learning Inside MILP Solvers

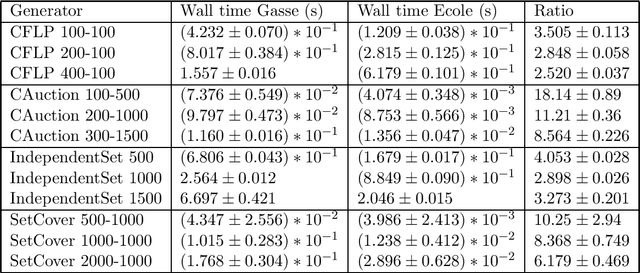
In this paper we describe Ecole (Extensible Combinatorial Optimization Learning Environments), a library to facilitate integration of machine learning in combinatorial optimization solvers. It exposes sequential decision making that must be performed in the process of solving as Markov decision processes. This means that, rather than trying to predict solutions to combinatorial optimization problems directly, Ecole allows machine learning to work in cooperation with a state-of-the-art a mixed-integer linear programming solver that acts as a controllable algorithm. Ecole provides a collection of computationally efficient, ready to use learning environments, which are also easy to extend to define novel training tasks. Documentation and code can be found at https://www.ecole.ai.

Combinatorial optimization and reasoning with graph neural networks

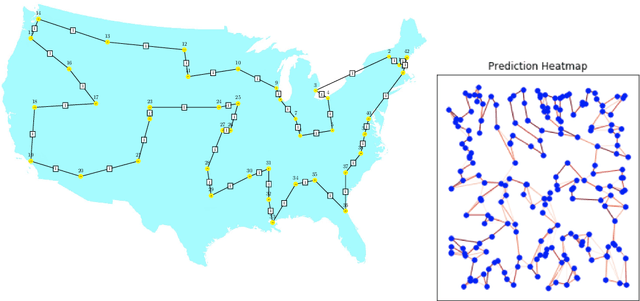
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring the fact that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning, especially graph neural networks (GNNs), as a key building block for combinatorial tasks, either as solvers or as helper functions. GNNs are an inductive bias that effectively encodes combinatorial and relational input due to their permutation-invariance and sparsity awareness. This paper presents a conceptual review of recent key advancements in this emerging field, aiming at both the optimization and machine learning researcher.

Ecole: A Gym-like Library for Machine Learning in Combinatorial Optimization Solvers

We present Ecole, a new library to simplify machine learning research for combinatorial optimization. Ecole exposes several key decision tasks arising in general-purpose combinatorial optimization solvers as control problems over Markov decision processes. Its interface mimics the popular OpenAI Gym library and is both extensible and intuitive to use. We aim at making this library a standardized platform that will lower the bar of entry and accelerate innovation in the field. Documentation and code can be found at https://www.ecole.ai.

Change Point Detection by Cross-Entropy Maximization

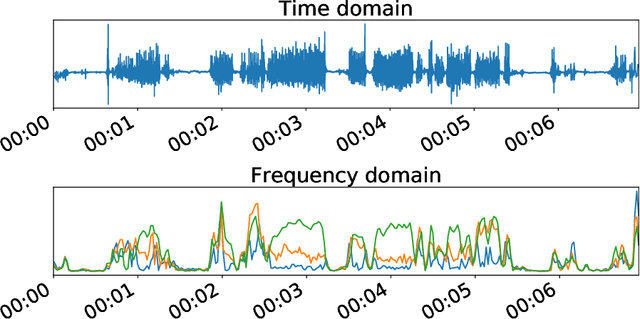
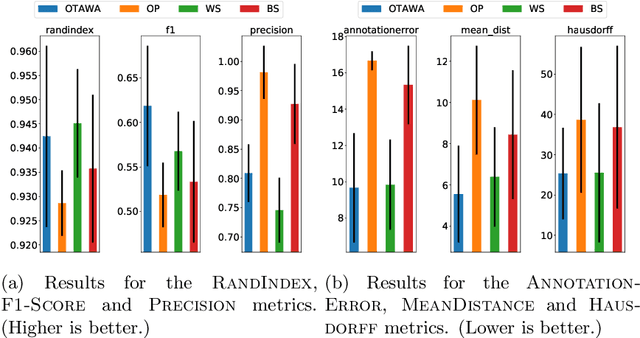
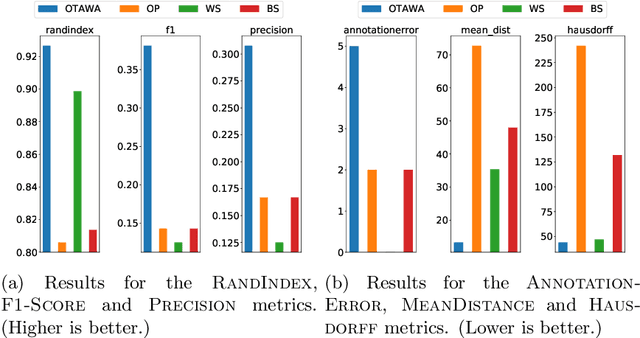
Many offline unsupervised change point detection algorithms rely on minimizing a penalized sum of segment-wise costs. We extend this framework by proposing to minimize a sum of discrepancies between segments. In particular, we propose to select the change points so as to maximize the cross-entropy between successive segments, balanced by a penalty for introducing new change points. We propose a dynamic programming algorithm to solve this problem and analyze its complexity. Experiments on two challenging datasets demonstrate the advantages of our method compared to three state-of-the-art approaches.

Exact Combinatorial Optimization with Graph Convolutional Neural Networks

Combinatorial optimization problems are typically tackled by the branch-and-bound paradigm. We propose a new graph convolutional neural network model for learning branch-and-bound variable selection policies, which leverages the natural variable-constraint bipartite graph representation of mixed-integer linear programs. We train our model via imitation learning from the strong branching expert rule, and demonstrate on a series of hard problems that our approach produces policies that improve upon state-of-the-art machine-learning methods for branching and generalize to instances significantly larger than seen during training. Moreover, we improve for the first time over expert-designed branching rules implemented in a state-of-the-art solver on large problems. Code for reproducing all the experiments can be found at https://github.com/ds4dm/learn2branch.