Learning to branch with Tree MDPs
Paper and Code
May 31, 2022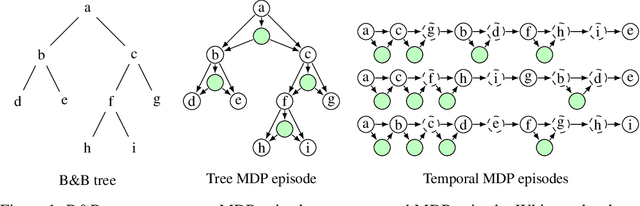

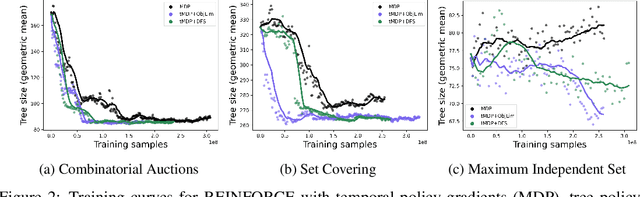
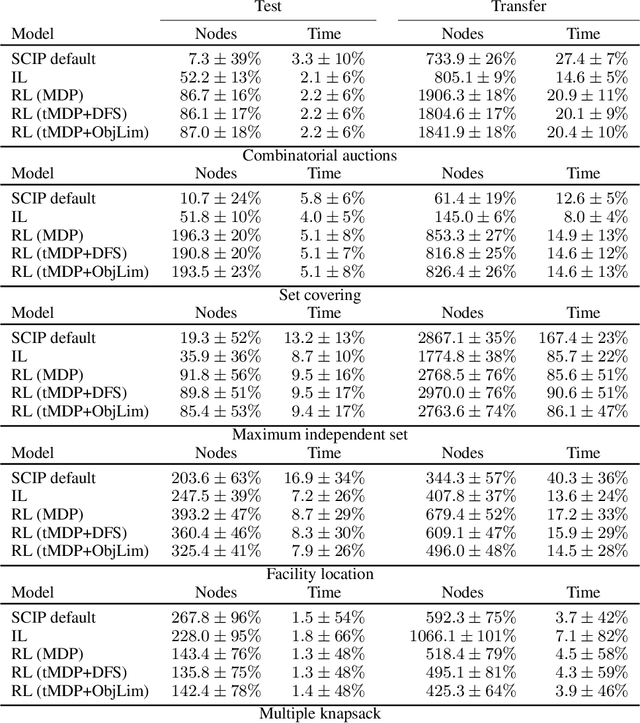
State-of-the-art Mixed Integer Linear Program (MILP) solvers combine systematic tree search with a plethora of hard-coded heuristics, such as the branching rule. The idea of learning branching rules from data has received increasing attention recently, and promising results have been obtained by learning fast approximations of the strong branching expert. In this work, we instead propose to learn branching rules from scratch via Reinforcement Learning (RL). We revisit the work of Etheve et al. (2020) and propose tree Markov Decision Processes, or tree MDPs, a generalization of temporal MDPs that provides a more suitable framework for learning to branch. We derive a tree policy gradient theorem, which exhibits a better credit assignment compared to its temporal counterpart. We demonstrate through computational experiments that tree MDPs improve the learning convergence, and offer a promising framework for tackling the learning-to-branch problem in MILPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge